Оператор множественного выбора switch
Общий вид:
switch (выражение)
{
case метка1: оператор1
case метка2: оператор2
default: операторЗ
}
Управление программой переходит к оператору, имеющему значение выражения в качестве метки. Затем программа продолжает выполняться, проходя остальные операторы, если снова не произойдет переключение направления. И выражение, и метки должны иметь целые значения (включая тип char), а метки быть либо константами, либо выражениями, состоящими только из констант. Если ни одна метка не соответствует значению выражения, управление передается оператору, помеченному default, если он существует. В ином случае управление передается оператору, следующему за оператором default.
Можно записывать более двух помеченных операторов, а вариант default не обязателен.
Пример: switch (number)
{
case 4: printf(" \n Хороший выбор! " ); break;
case 5: printf(" \n Неплохой выбор" ); break;
default: printf (" \n Плохой выбор" );
}
Наличие операторов break позволяет прекратить выполнение оператора switch и перейти к выполнению операторов, следующих за ним. Если убрать из примера все операторы break, то при значении number равном 4 на экран будут выданы все три сообщения.
Иногда, однако, это бывает полезным:
choice=getchar (); // Ввод одиночного символа switch (choice)
{
case 'A':
case 'B': printf(" \n Заглавная буква! " ); break;
case 'a':
case 'b': printf (" \n Строчная буква! " ); break;
}
Директива препроцессора #define
Директива #define необходима для задания символических констант и макроопределений.
Пример:
#include < stdio.h> #define TWO 2 //Константа #define MSG " \n Конец работы\ программы" // Обратная косая черта продолжает определение на следующую // строку
#define SQUARE(a) ((a)*(a)) //Макроопределение с аргументом #define PX printf(" \n Значение переменной %d", x); main ()
{
int x=TWO; PX
x=SQUARE(x);
PX
printf (MSG);
}
Препроцессор заменит в тексте программы все вхождения TWO, MSG, SQUARE(x), PX на 2, " \n Конец работы\ программы", ((x)*(x)), printf(" \n Значение переменной %d", x).
Порядок выполнения работы
В соответствии с вариантом задания выполнить экспериментальную часть лабораторной работы.
Для каждого варианта решить задачу с использованием конструкции if или if-else, а затем - с использованием конструкции switch.
Задания
Составить алгоритмы решения следующих задач:
| Варианты
| Задания
| |
| А
| Y = (x2+0.5)3 + arctg(x2 + 0.5) /3x + 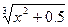 / cos(x2+0.5) + lg(x2 + 0.5)4 / cos(x2+0.5) + lg(x2 + 0.5)4
| | Б
| ì at2lnt, если 1≤ t ≤ 2
Y = í 1, если t < 1
î eatcosbt, если t > 2
| | В
| Известна длина ребра куба а. Найти длину диагонали основания, площадь боковой поверхности и объем куба.
| | Г
| Даны два действительных числа х, у (х 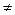 у). Если первое число больше второго, выдать признак
N = 100, в противном случае N = 0. у). Если первое число больше второго, выдать признак
N = 100, в противном случае N = 0.
| |
| А
| У= 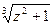 +cos +cos 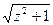 / (2z +1, 3) – 1, 5z + ln(z2 + 1) / (z +3, 2) – e-z -1 / (2z +1, 3) – 1, 5z + ln(z2 + 1) / (z +3, 2) – e-z -1
| | Б
| ì px2 – 7/(x2 +1), если x < 1, 3
Y = í ax3 + 7 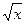 , если x = 1, 3
î lg(x +7 , если x = 1, 3
î lg(x +7 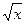 ), если x > 1, 3 ), если x > 1, 3
| | В
| По двум известным катетам найти гипотенузу, радиус описанной окружности и площадь прямоугольного треугольника.
| | Г
| Даны три числа, возвести в квадрат те из них, значения которых неотрицательны, отрицательные числа оставить без изменения.
| |
| А
| L = abc + 3, 2sinx + e-sinx –1/ abc + e-2abc +lg|abcd|
| | Б
| ì ax2 + bx +c, если x < 1, 2
Y = í a/x + 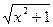 , если x = 1, 2
î (a + bx) , если x = 1, 2
î (a + bx) 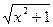 , если x > 1, 2 , если x > 1, 2
| | В
| Даны два числа. Найти среднее арифметическое кубов и среднее геометрическое модулей этих чисел.
| | Г
| Даны два числа а и в. Если а и в отрицательны, то каждое значение заменить его модулем; если отрицательно только одно из них, то оба значения увеличить на 0, 7; если оба значения неотрицательны, то оба значения увеличить в 10 раз.
| |
| А
| М = 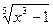 + 0, 5 arcsin(x3 –1) + e|-1+x| + 0, 5 arcsin(x3 –1) + e|-1+x|
| | Б
| ì 0, если 1≤ t ≤ 2
Y = í at, если t < 1
î eat + t4, если t > 2
| | В
| Дана сторона равностороннего треугольника. Найти его площадь.
| | Г
| Даны действительные числа а, в, с. Удвоить эти числа, если а≥ в≥ c, заменить их абсолютными значениями, если это не так.
| |
| А
| M = (0, 03x – 1)/3y, где y = |r2 –4| + lg|r2 –4| - 3arcsin(4-r2)/6, 8r
| | Б
| ì sin x, если x< -0, 8
Y = í 1/sin x, если -0, 8 ≤ x ≤ 0, 2
î sin x cos x, если x > 0, 2
| | В
| Найти площадь кольца, внутренний радиус которого равен r =20, а внешний R заданному числу (R > 20).
| | Г
| Даны три действительных числа l, m, n. Выбрать те из них, которые принадлежат интервалу (1; 3).
| |
| А
| M = lg|(y - 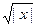 ) (cos |x| - y) / arccos ) (cos |x| - y) / arccos 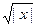 +1 +1
| | Б
| ì 0, если x ≤ 0
Y = í x2 - x, если 0 < x < 1
î x2 – sin px, в остальных случаях
| | В
| В равнобедренном треугольнике известны боковая сторона m, основание n. Найти его высоту и площадь.
| | Г
| Даны действительные числа x, y, z. Вычислить
U = max{x + y + z; xyz}
| |
| А
| M = pqr + 2sin2px + epqr +1 / pqr +ln |pqr|
| | Б
| ì 1, 5cos2x, если x < 1
Y = í 1, 8ax, если x = 1
| (x –2)2 +6, если 1< x < 2
î 3 tgx, в остальных случаях
| | В
| Найти площадь равнобочной трапеции с основаниями а и в и углом a при большем основании а.
| | Г
| Даны действительные числа а, в, с. Вычислить
Z = min2 {(a + b + c)/ 2; abc} + 1, 25
| |
| А
| Y = 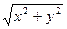 +3, 2 ln +3, 2 ln 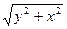 / 2, 7 – 0, 03arccos / 2, 7 – 0, 03arccos 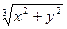
| | Б
| ì x3 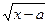 , если x > a
Y = í x sinax, если x = a
î e-axcosax, в остальных случаях , если x > a
Y = í x sinax, если x = a
î e-axcosax, в остальных случаях
| | В
| Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет, радиус вписанной окружности и площадь этого треугольника.
| | Г
| Даны три действительных числа. Выбрать те из них, которые принадлежат интервалу (1; 5).
| |
| А
| S = 2, 7 • 10 - 6 + | 1–x2 | + | 1- x2 | 3 / 3, 4 – 1, 5ln |1- x2| / x- – arcsin(x2-1)
| | Б
| ì bx -lgbx, если 0 < bx < 1
Y = í 1, если bx = 1
î bx +lgbx, в остальных случаях
| | В
| Даны действительные числа x, y, z. Утроить эти числа, если x ≤ y≤ z и заменить их абсолютными значениями, если это не так.
| | Г
| Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
| |
| А
| P = 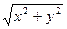 +5, 7lg | +5, 7lg | 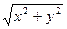 / 2, 8 x | -
- 0, 08sin / 2, 8 x | -
- 0, 08sin 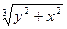
| | Б
| ì cos x, если x < 2, 3
Y = í 1, если x = 2, 3
î sin x lg x, в остальных случаях
| | В
| Даны три числа. Найти квадрат их среднего арифметического и среднеегеометрическое их модулей.
| | Г
| Даны действительные числа x, y, z. Вычислить
U = max{(x+y) / z; xyz} +1, 05 yz
| |
| А
| Q = 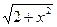 -0, 07arcctg(x2+2) +1, 27lg(x2+2)/(3, 7a-1)x + -0, 07arcctg(x2+2) +1, 27lg(x2+2)/(3, 7a-1)x + 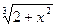
| | Б
| ì lg (x + 1), если x > 1, 1
Y = í 1, если x < 1, 1
î sin2 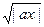 , в остальных случаях , в остальных случаях
| | В
| Даны три отличных от нуля числа, возвести в квадрат отрицательные, а положительные оставить без изменения.
| | Г
| Даны три действительных числа p, q, r. Выбрать из них те, которые принадлежат интервалу (-1; 3).
| | 1 12
| А
| Y = (1 + x 2 ) 3 + ( 1 – x 2) / сos | x | +
+ lg x / 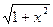 +arctg (x2+1) – 3e – x – 1 +arctg (x2+1) – 3e – x – 1
| | Б
| ì sin x lg x, если x > 2, 5
Y = í 1, если x = 2, 5
î cos x, в остальных случаях
| | В
| Число А составляет 2, 5% от числа В, которое в свою очередь составляет 6% от числа С, равного 216. Найти А и В.
| | Г
| Даны действительные числа а, в, с. Найти наименьшее из них: U = min{a, в, c}
| |
| А
| Z = (y3 - 0, 5)3 + arcctg(y3 - 0, 5) / 3y –
- 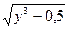 /arcsin(y3-0, 5) /arcsin(y3-0, 5)
| | Б
| ì abc, если a < 2, 7
Y = í (b+c)/a, если a = 2, 7
î (2c+b)/a2, в остальных случаях
| | \В
| Найти площадь кольца, внешний радиус которого равен R =23, а внутренний r заданному числу (0< r < R)
| | Г
| Если сумма трех попарно различных чисел x, y, z меньше 1, то меньшее из х и у заменить полусуммой у и z, иначе большее из х и z заменить на у4.
| |
| А
| Z= 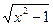 /3y, где у = /3y, где у = 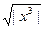 - arcsin - arcsin 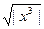 -8, 7x -8, 7x
| | Б
| ì a lg x + 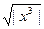 , если x > 0, 9
Y = í 1, если x = 0, 9
î 2a cos x +3x2, если х < 0, 9 , если x > 0, 9
Y = í 1, если x = 0, 9
î 2a cos x +3x2, если х < 0, 9
| | В
| Даны три числа. Найти куб их среднего арифметического и среднее геометрическое их кубов.
| | Г
| Даны три числа l, m, n. Вычислить
Z = min3{l+m; m+n; l+n}-0, 07lmn
| |
| А
| U=8m-0, 5n2/3, 8z, где z=lg|3-x2| + 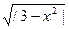 /(5, 5+x) + cos2(x2 – 3) /(5, 5+x) + cos2(x2 – 3)
| | Б
| ì 3a cos x, если x < 8, 3
Y = í 1/x3, если x = 8, 3
î sin x + lg x, в остальных случаях
| | В
| Даны действительные числа а, в, с. Удвоить их квадраты, если a> в> c, и заменить их абсолютными значениями, если это не так.
| | Г
| Даны три числа x, y, x. Вычислить
U = min2{x+y+z; xyz; x+2, 5yz}
| | | | | | |
Контрольные вопросы
1. Как на языке Си можно описать ветвление?
2. Охарактеризуйте арифметические, логические и битовые операции Си.
3. Какие операции знаете на языке Си
4. Что такое оператор множественного выбора
5. Для чего используется директива препроцессора #define
ЛАБОРАТОРНАЯ РАБОТА №3
|

