
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Информационные системы в методах оптимизацииСтр 1 из 5Следующая ⇒
Э.А. Кравцова Информационные системы в методах оптимизации Методические указания Дисциплина – «Методы оптимизации» Специальности – 230700.62 «Прикладная информатика», 231000.62 «Программная инженерия», 230400.62 «Информационные системы и технологии», 080801«Прикладная информатика (в экономике)», 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230100.62 «Информатика и вычислительная техника»
Допущено ФГБОУ ВПО «Госуниверситет-УНПК» для использования в учебном процессе в качестве методических указаний для высшего профессионального образования Орел 2013 Рецензент: к.т.н., доцент кафедры ИС О. В. Конюхова
Методические указания содержат описание пяти практических занятий по дисциплине «Методы оптимизации». Они посвящены выработке у студентов навыков разработки математических и информационных моделей процессов в предметной области; а также способствуют приобретению навыков экспериментальных исследований при выборе метода оптимизации, так же при решении типовых оптимизационных задач. Методические указания содержат теоретические сведения по рассматриваемым вопросам, практические примеры и справочную информацию, необходимую для выполнения лабораторных работ. Методические указания предназначены для студентов очной формы обучения специальностей 230700.62 «Прикладная информатика», 231000.62 «Программная инженерия», 230400.62 «Информационные системы и технологии», 080801«Прикладная информатика (в экономике)», 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230100.62 «Информатика и вычислительная техника».
Редактор Технический редактор
Орловский государственный технический университет Лицензия ИД 00670 от 5.01.2000
Подписано к печати Формат 60 Печать офсетная. Усл. печ. л.5, 6. Тираж 10 экз. Заказ №__________ Отпечатано с готового оригинал-макета на полиграфической базе ФГБОУ ВПО «Госуниверситет - УНПК»
© ФГБОУ ВПО «Госуниверситет - УНПК», 2012 © Кравцова Э.А. 2013
СОДЕРЖАНИЕ 1.Линейное программирование: симплекс – метод 4 2.Специальные задачи линейного программирования 19 3. Решение целочисленных задач 23 4. Решение задач многокритериальной оптимизации 27 5. Сетевая модель, расчет основных параметров сетевого графика 31 6.Теория игр 48 Литература 54 Практическое занятие №1 Линейное программирование: симплекс-метод решения задач линейного программирования, геометрическая интерпретация задач Практическое занятие №2 10)
|
Практическое занятие №3
Решение задач по нелинейной оптимизации. Метод множителей Лагранжа.
Практическое занятие №4
Сетевая модель, расчет основных параметров сетевого графика.
Построение сетевого графика
Сетевые графики представляют собой ориентированные графы, дугам или вершинам которых приписаны некоторые числовые значения.
Как правило, вершины, называемые событиями, соответствуют моментам времени начала или окончания одной или нескольких операций, а дуги – операциям.
Различают три вида событий: исходное, завершающее и промежуточное. Исходное – это такое событие, с которого начинается выполнение комплекса операций. Завершающее соответствует достижению конечной цели, т. е. завершению комплекса операций. Сетевые графики с несколькими завершающими событиями называются многоцелевыми. К промежуточным относятся все прочие события.
События, как правило, обозначаются кружками. Предполагается, что события не имеют продолжительности во времени.
Моментом свершения события считается момент окончания выполнения всех входящих в это событие операций. Пока не выполнены все входящие в событие операции, не может свершиться само событие, и, соответственно, не может быть начата ни одна из непосредственно следующих за ним операций.
Различают три вида операций:
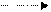
 1) действительная операция ( ) – процесс, требующий затрат времени и ресурсов (разработка проекта, подвоз материалов, выполнение монтажных работ и т. д.);
1) действительная операция ( ) – процесс, требующий затрат времени и ресурсов (разработка проекта, подвоз материалов, выполнение монтажных работ и т. д.);
2) операция - ожидание ( ) – процесс, требующий только затрат времени (затвердение бетона, естественная сушка штукатурки перед началом малярных работ, рост растений и т. д.);
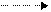 3) фиктивная операция ( ), или логическая зависимость, отражает технологическую или ресурсную зависимость в выполнении некоторых операций.
3) фиктивная операция ( ), или логическая зависимость, отражает технологическую или ресурсную зависимость в выполнении некоторых операций.
При построении сетевых графиков необходимо соблюдать определенные правила:
1) в сети не должно быть событий (кроме исходного), в которые не входит ни одна дуга;
2) не должно быть событий (кроме завершающего), из которых не выходит ни одной дуги;
3) сеть не должна содержать контуров;
4) любая пара событий сетевого графика может быть соединена не более чем одной дугой. Если изобразить одновременно выполняемые три различные операции 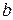 ,
, 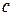 ,
,  с общими начальным и конечным событиями (Рис. 4.1), то возникает путаница из-за того, что различные операции имеют одно и то же обозначение (2, 5). В этом случае рекомендуется ввести дополнительные события и соединить их с последующими фиктивными операциями (Рис. 4.2);
с общими начальным и конечным событиями (Рис. 4.1), то возникает путаница из-за того, что различные операции имеют одно и то же обозначение (2, 5). В этом случае рекомендуется ввести дополнительные события и соединить их с последующими фиктивными операциями (Рис. 4.2);
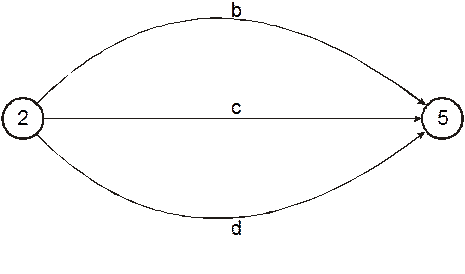
Рис. 4.1
5) номер начального события любой операции должен быть меньше номера ее конечного события.
Для отражения технологической или ресурсной зависимости в выполнении операций применяют фиктивные операции. Предположим, что операция 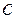 может выполняться после завершения операций
может выполняться после завершения операций 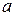 и
и 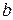 , а операция
, а операция 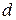 – только после завершения операции
– только после завершения операции 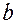 .
.
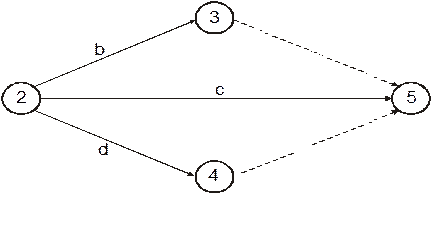
Рис. 4.2
Эта зависимость представлена на Рис. 4.3, из которого видно, что операция 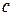 следует за операцией
следует за операцией 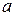 и фиктивной операцией (2, З).
и фиктивной операцией (2, З).
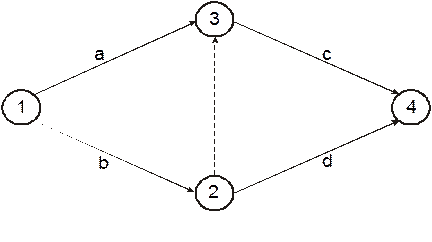 |
Рис. 4.3
В свою очередь, операция (2, 3) следует за операцией 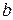 . Тогда в силу транзитивности выполнение операции
. Тогда в силу транзитивности выполнение операции 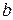 предшествует выполнению операции
предшествует выполнению операции 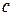 .
.
Построение сетевого графика начинается с составления списка операций (работ), подлежащих выполнению. Последовательность операций в списке является произвольной. Порядок нумерации операций осуществляется в соответствии с последовательностью их записи в списке. Перечень операций в зависимости от конкретных условий детализируется. Операции, включенные в список, характеризуются определенной продолжительностью, которая устанавливается на основе действующих нормативов или по аналогии с ранее выполнявшимися операциями. Такие временные оценки называются детерминированными. В случае отсутствия нормативных временных оценок определяются вероятностные оценки.
После составления списка операций приступают к процедуре построения сети.
Приведем пример построения простого сетевого графика. Рассмотрим проект, представленный с помощью следующей таблицы:
Таблица 4.1.
Описание составных работ проекта
| Работа | Непосредственно предшествующие работы | Время выполнения |
| A | --- | 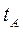
|
| B | --- | 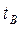
|
| C | B | 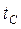
|
| D | A, C | 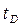
|
| E | C | 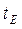
|
| F | C | 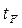
|
| G | D, E, F | 
|
Анализ данных, приведенных в этой таблице, последовательности и взаимозависимости работ, позволяет построить сетевой график представленный на рис. 4.4.
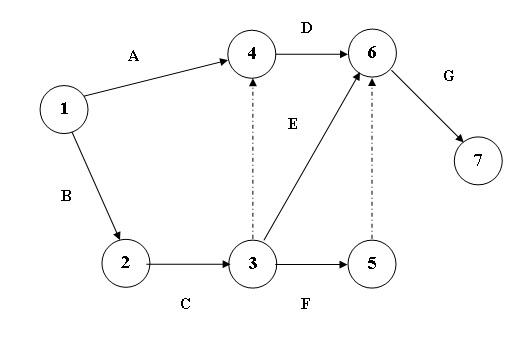
Рис. 4.4
В данном сетевом графике помимо работ, указанных в таблице, использованы две фиктивные работы (3, 4) и (5, 6), обозначенные штриховыми линиями. Эти работы не требуют времени на их выполнение и используются в графическом представлении проекта лишь для того, чтобы правильно отобразить взаимосвязь между работами.
Практическое занятие №5
Общие сведения
Раздел математики, изучающий конфликтные ситуации на основе их математических моделей, называется теорией игр. Можно также сказать, что теория игр - математическая теория конфликтных ситуаций, разрабатывающая рекомендации по наиболее рациональному образу действий каждого из участников в ходе конфликтной ситуации, т.е. таких действий, которые обеспечивали бы ему наилучший результат.
Игровые схемы можно применять во многих экономических ситуациях. Выигрышем могут при этом выступать величина прибыли, себестоимость, эффективность использования дефицитных ресурсов, производственных фондов, и т.д.
Существенным обстоятельством является то, что методы и рекомендации теории игр разработаны применительно к таким конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации теории игр становятся малоэффективными.
Анализ реальной конфликтной ситуации требует ее существенного (иногда радикального) упрощения – учета лишь наиболее существенных для конфликта факторов. В связи с этим, можно рассматривать игру как упрощенную математическую модель конфликтной ситуации, характеризующуюся наличием определенных правил. Эти правила устанавливают:
1. выбор образа действия игроков на каждом этапе игры;
2. информацию, которой обладает каждый игрок при осуществлении таких выборов;
3. плату для каждого игрока после завершения любого этапа игры.
Стратегией игры называется совокупность правил, определяющих поведение игрока на протяжении всей игры. Стратегии каждого игрока определяют результаты или платежи в игре; при этом каждый игрок имеет некоторое множество (конечное или бесконечное) возможных стратегий.
К числу определяющих характеристик игр можно отнести следующие:
1. имеется 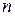 конфликтующих сторон (игроков), принимающих решения, интересы которых не совпадают;
конфликтующих сторон (игроков), принимающих решения, интересы которых не совпадают;
2. сформулированы правила выбора допустимых стратегий, известные игрокам;
3. определен набор возможных конечных состояний игры (например, выигрыш, проигрыш, ничья);
4. всем участникам игры (игрокам) заранее известны платежи, соответствующие каждому возможному конечному состоянию.
Конфликтные ситуации, встречающиеся в практике, порождают различные виды игр. Классификация игр возможна по разным признакам.
А) По количеству игроков. В игре может принимать участие любое конечное число игроков. Если игроков всего двое, или игроки объединяются в две группы, преследующие противоположные цели, то имеет место парная игра. В зависимости от количества стратегий в игре они делятся на конечные и бесконечные.
Б) В зависимости от взаимоотношений участников различают бескоалиционные (участники не имеют права заключать соглашения) и коалиционные игры (иногда используются синонимы – некооперативные и кооперативные игры соответственно).
В) По характеру выигрышей игры делятся на игры с нулевой суммой и ненулевой суммой. В играх с нулевой суммой общий капитал игроков не меняется, а лишь перераспределяется в ходе игры, в связи с чем сумма выигрышей равна нулю (при этом проигрыш рассматривается как отрицательный выигрыш). В играх с ненулевой суммой сумма выигрышей отлична от нуля.
Г) По виду функции выигрыша игры делятся на матричные, биматричные и др. В матричных играх (при двух участниках) выигрыши первого игрока задаются матрицей, в биматричных – выигрыши каждого игрока задаются своей матрицей.
Д) По количеству ходов игры делятся на одноходовые (выигрыш распределяется после одного хода каждого игрока) и многоходовые (выигрыш распределяется после нескольких ходов).
Стратегия игрока называется оптимальной, если она обеспечивает данному игроку при многократном повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш, независимо от поведения противника.
В дальнейшем мы ограничимся рассмотрением парных матричных игр с нулевой суммой. Задание стратегий двух игроков в парной игре такого типа полностью определяет ее исход, т.е. выигрыш одного или проигрыш другого. Как уже отмечалось, результаты конечной парной игры с нулевой суммой можно задавать матрицей, строки и столбцы которой соответствуют различным стратегиям 1-го и 2-го игроков соответственно, а ее элементы - выигрышам одной стороны (равные проигрышам другой). Эта матрица называется платежной матрицей или матрицей игры.
Игры без седловых точек
Итак, если матрица игры содержит седловую точку, то ее решение находится по принципу минимакса. Рассмотрим методику решения игры, в платежной матрице которой отсутствует седловая точка. Применение минимаксных стратегий каждым из игроков обеспечивает первому выигрыш не меньше 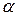 , а второму проигрыш не больше
, а второму проигрыш не больше 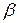 . Учитывая, что
. Учитывая, что 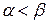 , естественно для игрока I желание увеличить выигрыш, а для игрока II – уменьшить проигрыш. Поиск такого решения приводит к применению сложной стратегии, состоящей в случайном применении двух и более чистых стратегий с определенными вероятностями. Такая сложная стратегия в теории игр называется смешанной. Смешанные стратегии игроков I и II будем обозначать, соответственно,
, естественно для игрока I желание увеличить выигрыш, а для игрока II – уменьшить проигрыш. Поиск такого решения приводит к применению сложной стратегии, состоящей в случайном применении двух и более чистых стратегий с определенными вероятностями. Такая сложная стратегия в теории игр называется смешанной. Смешанные стратегии игроков I и II будем обозначать, соответственно,
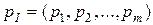 и
и 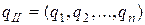
где 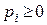 ,
, 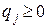 ‑ вероятности применения соответствующих чистых стратегий. Очевидно, должны выполняться условия нормировки для вероятностей
‑ вероятности применения соответствующих чистых стратегий. Очевидно, должны выполняться условия нормировки для вероятностей
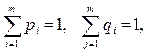
Одна из основных теорем теории игр утверждает, что любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение, возможно, в смешанных стратегиях. Из этой теоремы следует, что каждая конечная игра имеет цену. Обозначим ее так же, как чистую цену игры, через 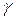 . Цена игры
. Цена игры 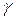 – средний выигрыш, приходящийся на одну партию, – всегда удовлетворяет условию
– средний выигрыш, приходящийся на одну партию, – всегда удовлетворяет условию 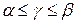 , т.е. лежит между нижней (
, т.е. лежит между нижней ( 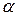 ) и верхней (
) и верхней ( 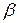 ) ценами игры. Следовательно, каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях, так же как и решение в чистых стратегиях, характеризуется тем, что каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему невыгодно.
) ценами игры. Следовательно, каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях, так же как и решение в чистых стратегиях, характеризуется тем, что каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему невыгодно.
Стратегии игроков, входящие в их оптимальные смешанные стратегии, называются активными.
5.5  Использование линейной оптимизации при решении матричных игр
Использование линейной оптимизации при решении матричных игр
Пусть игра 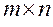 не имеет оптимального решения в чистых стратегиях, т.е. седловая точка отсутствует
не имеет оптимального решения в чистых стратегиях, т.е. седловая точка отсутствует 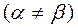 .
.
Будем считать, что все элементы платежной матрицы неотрицательны (если это не так, то можно ко всем элементам матрицы добавить некоторое число L, переводящее платежи в область неотрицательных значений - очевидно, при этом цена игры увеличится на L, а решение задачи не изменится). Таким образом, предполагаем, что 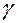 > 0.
> 0.
Будем искать решение игры в смешанных стратегиях
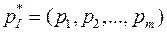 ;
; 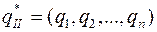
Применение игроком I оптимальной смешанной стратегии 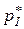 гарантирует ему, независимо от поведения игрока II, выигрыш, не меньший цены игры
гарантирует ему, независимо от поведения игрока II, выигрыш, не меньший цены игры 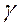 .
.
Пусть игрок II применяет свою активную чистую j-ю стратегию, а игрок I – свою оптимальную стратегию 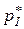 . Тогда средний выигрыш игрока I будет равен
. Тогда средний выигрыш игрока I будет равен
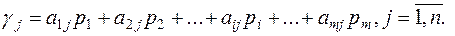
Учитывая, что 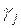
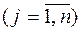 не может быть меньше
не может быть меньше 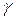 , запишем условия:
, запишем условия:
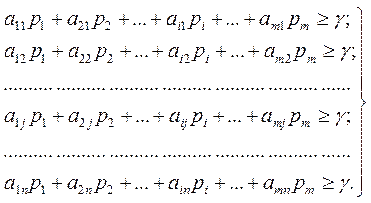 (5.4)
(5.4)
Разделив левую и правую части каждого из неравенств (5.4) на цену игры 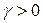 , получим
, получим
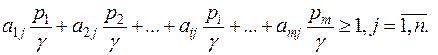 (5.5)
(5.5)
При использовании обозначений
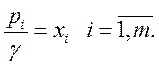 (5.6)
(5.6)
неравенства (5.5) примут вид
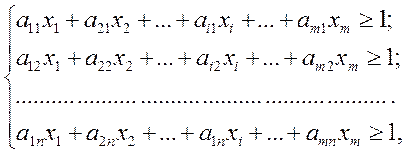
где, очевидно, все 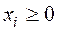 , так как
, так как 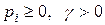 .
.
Из равенства
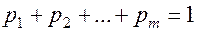
и в силу определения (5.6) следует, что переменные ( 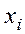 ) удовлетворяют условию
) удовлетворяют условию
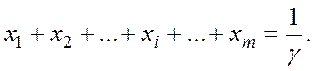
Учитывая, что игрок I стремится максимизировать 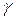 , получаем линейную функцию
, получаем линейную функцию
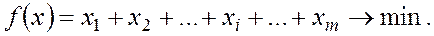 (5.8)
(5.8)
Таким образом, задача решения игры свелась к следующей задаче линейной оптимизации: найти неотрицательные значения переменных 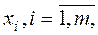 минимизирующие линейную функцию (5.8) и удовлетворяющие ограничениям (5.7).
минимизирующие линейную функцию (5.8) и удовлетворяющие ограничениям (5.7).
Из решения задачи линейной оптимизации легко найти цену игры 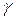 и оптимальную стратегию
и оптимальную стратегию 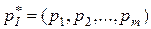 игрока I:
игрока I:
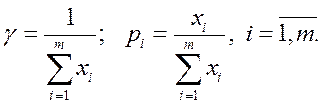
В свою очередь, оптимальная стратегия игрока II
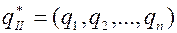
может быть найдена из выражения
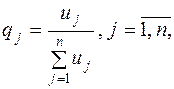
где 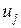 - неотрицательные переменные задачи линейной оптимизации
- неотрицательные переменные задачи линейной оптимизации
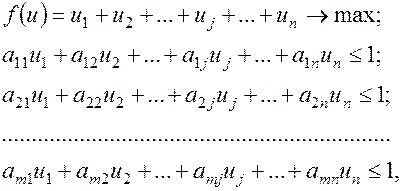
которая является двойственной по отношению к задаче, представленной условиями (5.7) и (5.8).
В этой системе неравенств переменные
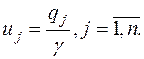
Таким образом, оптимальные стратегии
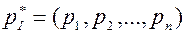 и
и 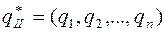
игры с платежной матрицей 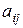 (
( 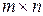 ) могут быть найдены путем решения симметричной пары двойственных задач линейной оптимизации.
) могут быть найдены путем решения симметричной пары двойственных задач линейной оптимизации.
Исходная задача Двойственная задача
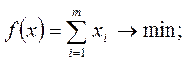
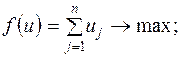
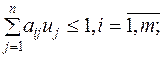
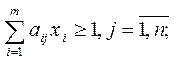
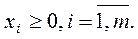
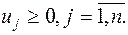
Цена игры и вероятности применения стратегий игроками I и II равны
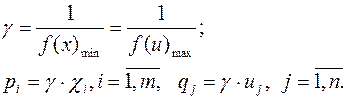
5.6 Задачи для самостоятельного решения
Путем сведения двойственных задач линейного программирования найти оптимальные смешанные стратегии и цену игры матричных игр с такими платежными матрицами:
| 1) | -8 | 2) | -2 | -5 | 3) | -1 | 4) | -6 | 5) | -3 | ||||
| -8 | -4 | -4 | -3 | -1 |
| 6) | -3 | 7) | 8) | -1 | 9) | -1 | |||||||||
| -5 | -3 | -1 | |||||||||||||
| -9 | -1 | -2 | -3 |
ЛИТЕРАТУРА
1. Сборник задач по высшей математике для экономистов: Учебное пособие /Под ред. В.И.Ермакова. – М.: ИНФРА-М, 2001 (и поздние издания)
2. Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию.– Мн: Вышэйшая школа, 2001
3. Налбандян Ю.С. Руководство к решению задач по линейной алгебре. Метод. указания для студентов специальности «Менеджмент организаций». - Ростов-на-Дону: 2007.
4. Общий курс высшей математики для экономистов: Учебник/Под ред. В.И.Ермакова. – М.: ИНФРА-М, 2000 (и поздние издания).
5. Исследование операций в экономике / Под ред. Н.Ш.Кремера – М.: ЮНИТИ, 1997 (и поздние издания).
6. Солодовников А.С., Бабайцев П.А., Браилов А.В Математика в экономике. Ч.1. М.: Финансы и статистика, 2001
Э.А. Кравцова
Информационные системы в методах оптимизации
Методические указания
по выполнению практических занятий
Дисциплина – «Методы оптимизации»
Специальности – 230700.62 «Прикладная информатика», 231000.62 «Программная инженерия», 230400.62 «Информационные системы и технологии», 080801«Прикладная информатика (в экономике)», 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230100.62 «Информатика и вычислительная техника»
Допущено ФГБОУ ВПО «Госуниверситет-УНПК» для использования в учебном процессе в качестве методических указаний для высшего профессионального образования
Орел 2013
Авторы: старший преподаватель кафедры ИС Э.А.Кравцова
Рецензент: к.т.н., доцент кафедры ИС О. В. Конюхова
Методические указания содержат описание пяти практических занятий по дисциплине «Методы оптимизации». Они посвящены выработке у студентов навыков разработки математических и информационных моделей процессов в предметной области; а также способствуют приобретению навыков экспериментальных исследований при выборе метода оптимизации, так же при решении типовых оптимизационных задач. Методические указания содержат теоретические сведения по рассматриваемым вопросам, практические примеры и справочную информацию, необходимую для выполнения лабораторных работ.
Методические указания предназначены для студентов очной формы обучения специальностей 230700.62 «Прикладная информатика», 231000.62 «Программная инженерия», 230400.62 «Информационные системы и технологии», 080801«Прикладная информатика (в экономике)», 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230100.62 «Информатика и вычислительная техника».
Редактор
Технический редактор
Орловский государственный технический университет
Лицензия ИД 00670 от 5.01.2000
Подписано к печати Формат 60 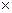 84 1\16
84 1\16
Печать офсетная. Усл. печ. л.5, 6. Тираж 10 экз.
Заказ №__________
Отпечатано с готового оригинал-макета
на полиграфической базе ФГБОУ ВПО «Госуниверситет - УНПК»
© ФГБОУ ВПО «Госуниверситет - УНПК», 2012
© Кравцова Э.А. 2013
СОДЕРЖАНИЕ
1.Линейное программирование: симплекс – метод 4
2.Специальные задачи линейного программирования 19
3. Решение целочисленных задач 23
4. Решение задач многокритериальной оптимизации 27
5. Сетевая модель, расчет основных параметров сетевого графика 31
6.Теория игр 48
Литература 54
Практическое занятие №1
Последнее изменение этой страницы: 2017-04-13; Просмотров: 546; Нарушение авторского права страницы