ПОСТРОЕНИЕ МОДЕЛЕЙ ГИДРОДИНАМИЧЕСКИХ И ТЕПЛОВЫХ ПРОЦЕССОВ

УРАВНЕНИЕ ГИДРАВЛИЧЕСКОЙ ЕМКОСТИ

Пусть элементом системы будет гидравлическая емкость резервуар с жидкостью (рис.1, а), в котором должен поддерживаться постоянным уровень жидкости.

а)   б)

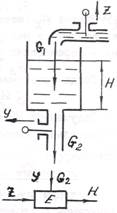
Рис.1

Регулируемая величина - выходная переменная элемента - высота уровня жидкости Н, изменяющаяся благодаря изменению расходов G₁ и G₂,

Расходы жидкости G₁ и G₂ (м³/с) зависят от перемещений z и y соответствующих клапанов; кроме того, расход G₂ зависит от напора. Таким образом,

 

G₁ = G₁ (z)

и

G₂ = G₂ (у, Н)

 

Перемещения клапанов z и y являются входными величинами элемента.

Блок-схема емкости изображена на рис.1, б.

В установившемся режиме G₁ = G₂ и высота уровня жидкости остается неизменной (Н = const). При изменении какого-либо из расходов или одновременном изменении их высота уровня изменяется.

Составим уравнение материального баланса емкости.

За малый промежуток времени dt количество жидкости в резервуаре измениться на. dG м³, так как в емкость поступит G₁dt м³ жидкости, а сольется G₂dt м³, то есть

dG = (G₁ - G₂) dt

 

Но изменение количества жидкости в резервуаре можно представить как произведение площади поперечного сечения резервуара и изменения высоты уровня

 

dG = S dH

 

поэтому можно записать

 

S dH = (G₁ - G₂) dt или .

 

Подставив вместо G₁ и G₂ их выражения, получим уравнение емкости

 

 

Предположим, что клапан подачи жидкости имеет такой профиль, что расход G₁, пропорционален z:

G₁ = аz.

 

Расход G₂ через сливной клапан пропорционален корню квадратному из напора Н и при соответствующем профиле клапана - перемещению у:

 

 

Тогда уравнение емкости запишется в виде

 

 

Полученное уравнение является нелинейным уравнением, следовательно, емкость представляет собой нелинейный элемент.

ОПИСАНИЕ ТЕПЛОПЕРЕНОСА

Рассмотрим вопрос математического описания теплопереноса с учетом аналогии и взаимосвязи этого процесса с массопереносом Имеем поле температур

 

T = f (х, у, z, t),

 

где х, у, z — координаты точки в пространстве;

t — время.

Рассмотрим в трехмерном пространстве две изотермические поверхности, все точки которых имеют температуры Т и Т+Δ Т соответственно. Изменение температур в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности, причем наиболее резкое изменение температуры происходит в направлении нормали n к изотермической поверхности. Вектор, длина которого равна пределу отношения изменения температуры Δ Т к расстоянию Δ n между изотермическими поверхностями по нормали, а направление совпадает с направлением нормали, называется температурным градиентом:

 

т. е. grad T — вектор, направленный по нормали к поверхности уровня и численно равный скорости изменения Т по этому направлению. Для скалярного поля Т (х, у, z) этот вектор вычисляется по следующей формуле

 

 

где — единичные векторы, направленные по координатным осям х, у, z.

Передача тепла в неподвижной среде описывается законом Фурье

 

q_T = — λ grad T,

где q_T — тепловой поток (количество вещества, передаваемое через единицу поверхности в единицу времени);

λ — коэффициент теплопроводности.

В чистом виде такой процесс можно наблюдать лишь в твердых телах. В газах и жидкостях на этот процесс оказывает влияние движения среды, т. е. свободная и вынужденная конвекция. С учетом конвекции закон Фурье можно представить в следующем виде:

q_T = — λ grad T + с_р ρ w T,

 

где с_р — теплоемкость при постоянном давлении;

ρ — плотность среды;

w — скорость потока.

Это уравнение целесообразно использовать при ламинарном (Re< 2300) и переходном (2300 < Re < 10000) режиме движения потока.

Выше были рассмотрены процессы передачи тепла внутри среды с определенными физическими свойствами. Остановимся на вопросе теплообмена между средами.

Для этой цели часто пользуются эмпирическим законом теплопереноса

 

q_T = α Δ T

 

где Δ T — разность температур;

α — коэффициент теплоотдачи.

Теплообмен между двумя поверхностями, нагретыми до температур Т₁ и Т₂ при преобладании теплопередачи излучением в соответствие с законом Стефана — Больцмана описывается уравнением

 

q_И = ε С₀(Т₁⁴ – Т₂⁴),

 

где ε — приведенная степень черноты;

С₀ — коэффициент лучеиспускания абсолютно черного тела.

Чаще всего передача тепла теплопроводностью, конвекцией и излучением наблюдается одновременно. В этом случае пользуются общим коэффициентом теплоотдачи, представляя тепловой поток в виде

 

q₀ = α ₀(Т₁ – Т₂) = (α _с + α _л) (Т₁ – Т₂)

 

где α ₀ — общий коэффициент теплоотдачи;

α _с и α _л — коэффициенты теплоотдачи соприкосновением и лучеиспусканием.

В ряде случаев, особенно при большой доли теплопередачи излучением, лучшие результаты может дать уравнение по структуре аналогичное

 

q_И = ε С₀(Т₁⁴ – Т₂⁴), т.е. q₀ = (ε _с + ε ) С₀(Т₁⁴ – Т₂⁴).

 

Влияние конвективного теплообмена учитывается здесь увеличением степени черноты на некоторую величину ε _с.

Следует заметить, что лишь в некоторых относительно простых случаях можно пользоваться табличными значениями указанных коэффициентов. В большинстве же реальных металлургических агрегатов эти коэффициенты приходится определять экспериментально-статистическими методами. Однако роль теоретических представлений и здесь остается решающей, так как они позволяют определить адекватную структуру математической модели.

МОДЕЛИ СТРУКТУРЫ ПОТОКОВ

 

СТРУКТУРА ПОТОКОВ в аппаратах непрерывного действия, существенно влияет на химимческие процессы, тепло-и массообмен. Для процессов в многофазных потоках важно взаимное направление движения фаз (противоток, прямоток и др.) и геометрические формы движущихся объемов (пленки, струи, капли, пузыри). При рассмотрении переноса процессов существенны режим течения (ламинарный, турбулентный) и связанная с ним проблема пограничного слоя. Большое значение имеют различия во времени пребывания частиц потока в рабочем объеме и их взаимное перемешивание в результате нестационарности поля скоростей, неравномерности распределения скоростей и их разнонаправленности. В частицах потока, покидающих рабочий объем быстрее других, процесс оказывается незавершенным; в частицах, задерживающихся в этом объеме, он проходит глубже. Поскольку скорость процесса обычно снижается во времени, его незавершенность определяется долей частиц с малым временем пребывания. Отрицательное влияние неравномерности распределения времени пребывания тем сильнее, чем выше требуемая степень незавершенности процесса.

Перемешивание в потоках подразделяют по направлению на поперечное и продольное, а также по уровню - перемешивание на макроуровне (смешивающиеся частицы сохраняют свою индивидуальность) и на микроуровне (происходит гомогенизация частиц). Поперечное перемешивание, как правило, связана с турбулентностью; оно интенсифицирует массо- и теплоперенос. Продольное перемешивание - взаимное смешение элементов потока, поступивших в аппарат в разные моменты времени. Оно приводит к выравниванию профилей концентраций и температур по длине потока, к неравномерности распределения времен пребывания, часто уменьшает движущую силу процесса и снижает его эффективность. Для подавления продольного перемешивания и усиления поперечного применяют секционирование потока с помощью соответствующих устройств.

Для анализа химико-технологических процессов используют модели структуры потоков разной степени идеализации; простейшие из них - идеальное вытеснение и идеальное смешение. В первом случае предполагается отсутствие продольного перемешивания при полном поперечном, время пребывания всех частиц одинаково. Эта модель удовлетворительно описывает, например, множественные процессы в длинных тpyбax, особенно заполненных зернистыми слоями. В модели идеального смешения полагают, что элементы потока при поступлении в аппарат мгновенно и равномерно смешиваются со всем его содержимым, концентрации и температура одинаковы во всех точках объема. К этой модели близки, например, потоки в аппаратах с интенсивным механическим перемешиванием.

Упомянутые модели - крайние случаи условий смешения в потоке. Промежуточные случаи описывают модели, выбор которых определяется физ. картиной процесса и степенью сложности расчетов. Диффузионные модели представляют поток как вытеснение, на которое накладывается перенос в продольном (однопараметричная модель) или в продольном и поперечном (двухпараметричная модель) направлениях, причем перенос формально описывается уравнениями диффузии. Ячеечная модель представляет поток как последовательность одинаковых ячеек идеального смешения, причем число ячеек подбирается так, чтобы отразить влияние продольного перемешивания. Ячеечная модель удовлетворительно описывает потоки в секционированных аппаратах; как простую расчетную схему ее иногда используют и для иных потоков. Более сложные потоки описываются комбинированными моделями (схемные соединения простых моделей).

Каждой модели структуры потоков отвечает уравнение или система уравнений, позволяющие рассчитывать процесс в потоке и необходимый объем аппарата. Эти уравнения содержат параметры моделей (эффективный коэффициент диффузии, число ячеек и др.), для определения которых применяют различные методы. Например, на входе потока вводят по определенному закону (импульсному, ступенчатому и др.) индикатор, а на выходе регистрируют отклик - изменение концентрации индикатора во времени. Обработка отклика методами статистики позволяет оценить закон распределения времени пребывания и найти параметры модели.

Сведения о структуре потоков особенно важны при моделировании промышленных аппаратов. При переходе к ним от малых установок следует учитывать изменение структуры потоков. Знание параметров структуры потоков и физико-химических характеристик процессов позволяет расчетным путем исследовать и прогнозировать поведение аппаратов и определять оптимальные условия их работы.

 

⇐ Предыдущая123Следующая ⇒

Поделиться: