
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Обобщенные приемы познавательной деятельности процесса поиска решения задач: функциональный подход.Стр 1 из 7Следующая ⇒
Обобщенные приемы познавательной деятельности процесса поиска решения задач: функциональный подход. 2.Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов на плоскости Под динамизацией мы понимаем процесс исследования и открытия свойств геометрических объектов с помощью изменения определяющих их параметров. Типы динамических задач? 1. Установление области определения. 2. Установление области изменения при заданной области определения. Например: Найти геометрическое место центров вписанных окружностей (область значений) при заданном перемещении вершин треугольника (область определения). Найти множество значений, которые принимает площадь треугольника при том же движении. 3. Установление способа движения по множеству значений, при указанном способе движения по области определения. Обобщенные приемы познавательной деятельности процесса поиска решения задач Динамизацию геометрических объектов можно использовать двояко: как цель (при этом формулируются динамические задачи), как средство (при этом любая нединамическая задача проходит через динамику, отвлекаясь потом от последней). Для решения задач обоих классов используются достаточно обобщенные приемы познавательной деятельности учащихся. Эти приемы, носят достаточно обобщенный характер и могут служить ориентировочной основой действий учащихся в ходе решения различных типов задач. Это задачи на: 1. Опровержение ложных формул или других ложных утверждений. 2. На отыскание неизвестных элементов и отношений между ними. 3. Задачи на доказательство. 4. Задачи на построение. 5. Задачи на определенность геометрической фигуры. 6. Задачи на отыскание геометрического места точек. 7. Задачи на установление функциональных зависимостей. Задача: На плоскости даны координаты точек А, С, D. Точки А,В,С,D лежат на параболе. При каких значениях координат точки В(хо,уо) площадь четырехугольника ABCD будет наибольшей.
3.Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов в пространстве Под динамизацией мы понимаем процесс исследования и открытия свойств геометрических объектов с помощью изменения определяющих их параметров. Типы динамических задач? 1) Установление области определения. 2) Установление области изменения при заданной области определения. 3) Установление способа движения по множеству значений, при указанном способе движения по области определения. Виды задач Несмотря на уникальность олимпиадных задач, можно всё-таки выделить несколько типичных идей, составляющих суть задач. Разумеется, по определению, такой список будет неполным. · Задачи на инвариант · Задачи - игры · Задачи, решаемые с использованием принципа Дирихле. · Комбинаторика · Задачи на раскраски, укладки и замощения · Диофантовые ур-ния · Геометрические задачи. И т.д.
Методы решения Не существует единого метода решения олимпиадных задач. Напротив, количество методов постоянно пополняется. Некоторые задачи можно решить несколькими разными методами или комбинацией методов. Характерная особенность олимпиадных задач в том, что решение с виду несложной проблемы может потребовать применения методов, использующихся в серьёзных математических исследованиях. Ниже приводится (по определению) неполный список методов решения олимпиадных задач: · Доказательство от противного · Принцип Дирихле · Решение методами другой науки (замена алгебраической задачи геометрической или физической и наоборот) · Правило крайнего · Шахматы, Решение «с конца», выяснение стратегии (задачи-игры) · Поиск инварианта · Математическая индукция · Метод итераций · Подсчёт двумя способами · Метод аналогий · Провокационный метод · Алгебраический и аналитический методы, на треугольники, на четырёхугольники, вписанные и описанные окружности около тр-ков и 4-ков, метод площадей, подобие треугольников, равенство углов(геометрия) · Вспомогательная раскраска Метод раскраски. Суть метода вспомогательной раскраски состоит в следующем. Раскрасив некоторые ключевые элементы, которые фигурируют в задаче в несколько цветов, исследовать, что будет происходить, если выполнять условия задачи. Цвет позволяет значительно упростить понимание процесса, фигурируемого в условии, и зачастую приводит к решению. Этот метод позволяет эффективно решать ряд задач, в частности, игровые и шахматные задачи.
Диофантовы уравнения. ДИОФАНТОВЫ УРАВНЕНИЯ - алгебраические уравнения или системы алгебраических уравнений, решения которых отыскиваются в целых или рациональных числах. Обычно предполагается, что Д. у. имеют число неизвестных, превосходящее число уравнений, в связи с чем они называются также неопределенными уравнениями. Диофантовыми уравнениями называются уравнения вида При исследовании диофантовых уравнений обычно ставятся следующие вопросы: 1. имеет ли уравнение целочисленные решения; 2. конечно или бесконечно множество его целочисленных решений; 3. решить уравнение на мн-ве целых чисел, т. е. найти все его целочисленные решения; 4. решить уравнение на множестве целых положительных чисел; 5. решить уравнение на множестве рациональных чисел. Решить уравнение в целых числах Решение: свободный член уравнения 1. Делители свободного члена уравнения: ±1. Старший коэффициент уравнения 1. Положительные делители старшего коэффициента: 1. Следовательно, все целые корни уравнения находятся среди чисел {-1,1}. Подставляя Диофантовы уравнения с двумя и более неизвестными подразделяются на уравнения первой степени и уравнения высших степеней. Д. у. первой степени или так называемые линейные уравнения имеют вид Простейшим видом уравнений в целых числах являются уравнения вида Задачи - игры Игра — тип олимпиадных задач по математике, в которых требуется проанализировать стратегию игры и/или назвать победителя этой игры. Обычно заканчивается традиционным вопросом: «кто выиграет при правильной игре?» Как правило, в задачах этого типа игры: 1. детерминированы 2. финитны 3. с полной информацией 4. включают ровно двух участников 5. с невозможной (по правилам) ничьей Указанные задачи, как правило, не предполагают знания теории игр. Тем не менее, отдельные положения теории игр — интуитивно очевидные — могут использоваться. Игровые олимпиадные задачи решаются при помощи следующих разделов математики: · Комбинаторика · Целые числа · Графы и раскраски · Диофантовые уравнения · Динамизация · Принцип Дирихле Игровые задачи можно разделить на несколько видов. 1ый вид – это шахматные задачи. 2ой вид игровых задач – это задачи, в которых выигрышность доказывается «с конца», 3ий вид задач – это задачи, в которых используется термин «правильная игра». «Правильной игрой» называется выигрышная стратегия, придерживаясь которой игрок выиграет при любых ответных действиях противника. Задача. В кубе АВСD
 – куб – куб


Найти:
1) Введём прямоугольную систему координат, как показано на рисунке 2) Общность задачи не нарушится, если ребро куба обозначить за 2 3) Найдём координаты нужных точек А(2;0;0) Е(2;1;2) F(1;2;2) B(2;2;0) 4) Введём направляющие векторы прямых АЕ и BF, и найдём их координаты:
26. Векторно-координатный метод определения угла между прямой и плоскостью.
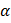 и не перпендикулярна и не перпендикулярна 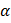 , то углом между прямой АВ и плоскостью , то углом между прямой АВ и плоскостью 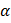 наз. угол между прямой АВ и её проекцией на пл-сть наз. угол между прямой АВ и её проекцией на пл-сть 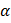 . .
АВ
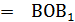
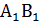 = = 
 = = 
  = = 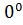 Алгоритм векторно-координатного метода: 1). Используя особенности заданной фигуры ввести в пространстве прямоугольную систему координат 2). Ввести направляющий вектор прямой 3). Ввести нормальный вектор плоскости 4). Найти 27.Векторно-координатный метод определения угла между двумя плоскостями
Алгоритм векторно-координатного метода: 1). Ввести прямоугольную систему координат 2.) Ввести нормальные векторы 3.) Вычислить косинус угла между векторами 4.) Найти по формуле Задача: В прямоугольном параллелепипеде АВСD
Дано: прямоугольный параллелепипед АВ = 6 ВС = 6 Найти:
Решение: 1) Введём прямоугольную систему координат, как показано на рисунке 2) Найдём координаты нужных точек: В(0;0;0) A(6;0;0) C(0;6;0) 3) Введём нормальный вектор плоскости Введём нормальный вектор плоскости Найдём одно из решений системы (1) Если 4) Для нахождения косинуса угла между прямыми воспользуемся формулой:
28.Векторно-координатный метод определения расстояния между фигурами.
Площадь сферы
Описанные многогранники. Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника. Теорема. В правильную n-угольную пирамиду можно вписать сферу. Доказательство
Общие замечания о положении центра шара. 1. Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника. 2. Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника. Вписанные многогранники.
Теорема.Треугольная пирамида имеет единственную описанную сферу. Доказательство Рисунок 5.6.1
Теорема. Для того, чтобы пирамида была вписанной в сферу, необходимо и достаточно, чтобы ее основанием был вписанный в окружность многоугольник. Следствие.Любая правильная пирамида является вписанной. Теорема. Пусть центр сферы, описанной вокруг пирамиды, лежит на прямой, проходящей через высоту пирамиды. Тогда 1. b2 = 2RH, 2. r2 = H(2R – H), где R – радиус описанной сферы, H и b – соответственно высота и боковое ребро пирамиды, а r – радиус окружности, описанной вокруг основания пирамиды.
Общие замечания о положении центра шара. 1. Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника. 2. Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника. Обобщенные приемы познавательной деятельности процесса поиска решения задач: функциональный подход. 2.Обобщенные приемы познавательной деятельности процесса поиска решения задач: динамизация геометрических объектов на плоскости Под динамизацией мы понимаем процесс исследования и открытия свойств геометрических объектов с помощью изменения определяющих их параметров. Типы динамических задач? 1. Установление области определения. 2. Установление области изменения при заданной области определения. Например: Найти геометрическое место центров вписанных окружностей (область значений) при заданном перемещении вершин треугольника (область определения). Найти множество значений, которые принимает площадь треугольника при том же движении. 3. Установление способа движения по множеству значений, при указанном способе движения по области определения. |
Последнее изменение этой страницы: 2019-05-08; Просмотров: 320; Нарушение авторского права страницы