
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Основные способы (методы) решения задач с параметром?
Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения. Комментарий. По мнению авторов, аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им. Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a). Комментарий. Исключительная наглядность и красота графического способа решения задач с параметром настолько увлекает изучающих тему «Задачи с параметром», что они начинают игнорировать другие способы решения, забывая общеизвестный факт: для любого класса задач их авторы могут сформулировать такую, которая блестяще решается данным способом и с колоссальными трудностями остальными способами. Поэтому на начальной стадии изучения опасно начинать с графических приемов решения задач с параметром. Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение. 23. Применение векторов к решению аффинных задач в пространстве. Применение векторов к решению метрических задач в пространстве.
25. Векторно-координатный метод определения угла между прямыми.

 AOB AOB
Алгоритм векторно-координатного метода: 1). Введём прямоугольную систему координат и единицу измерения 2). Найдём координаты нужных точек 3).Найдём координаты направляющих векторов скрещивающихся прямых 4). Найдём угол между векторами Задача. В кубе АВСD
 – куб – куб


Найти:
1) Введём прямоугольную систему координат, как показано на рисунке 2) Общность задачи не нарушится, если ребро куба обозначить за 2 3) Найдём координаты нужных точек А(2;0;0) Е(2;1;2) F(1;2;2) B(2;2;0) 4) Введём направляющие векторы прямых АЕ и BF, и найдём их координаты:
26. Векторно-координатный метод определения угла между прямой и плоскостью.
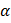 и не перпендикулярна и не перпендикулярна 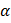 , то углом между прямой АВ и плоскостью , то углом между прямой АВ и плоскостью 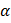 наз. угол между прямой АВ и её проекцией на пл-сть наз. угол между прямой АВ и её проекцией на пл-сть 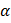 . .
АВ
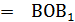
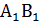 = = 
 = = 
  = = 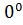 Алгоритм векторно-координатного метода: 1). Используя особенности заданной фигуры ввести в пространстве прямоугольную систему координат 2). Ввести направляющий вектор прямой 3). Ввести нормальный вектор плоскости 4). Найти 27.Векторно-координатный метод определения угла между двумя плоскостями
Алгоритм векторно-координатного метода: 1). Ввести прямоугольную систему координат 2.) Ввести нормальные векторы 3.) Вычислить косинус угла между векторами 4.) Найти по формуле Задача: В прямоугольном параллелепипеде АВСD
Дано: прямоугольный параллелепипед АВ = 6 ВС = 6 Найти:
Решение: 1) Введём прямоугольную систему координат, как показано на рисунке 2) Найдём координаты нужных точек: В(0;0;0) A(6;0;0) C(0;6;0) 3) Введём нормальный вектор плоскости Введём нормальный вектор плоскости Найдём одно из решений системы (1) Если 4) Для нахождения косинуса угла между прямыми воспользуемся формулой:
28.Векторно-координатный метод определения расстояния между фигурами.
|
Последнее изменение этой страницы: 2019-05-08; Просмотров: 269; Нарушение авторского права страницы