Раздел 1. Элементы линейной алгебры и аналитической геометрии

Раздел 1. Элементы линейной алгебры и аналитической геометрии

Глава 1. Матрицы и определители

Понятие матрицы

Прямоугольная таблица, состоящая из чисел, расположенных в m строках и n столбцах, называется матрицей. Матрицы обозначаются заглавными латинскими буквами, например: . Числа m и n называются порядками матрицы. Если m = n, то матрица называется квадратной порядка n, иначе – прямоугольной. Числа , входящие в состав матрицы, называются ее элементами, причем i – номер строки, j – номер столбца.

Строчная матрица имеет размер , а столбцовая матрица – .

Матрица , полученная из матрицы А заменой в ней строк на столбцы с сохранением порядка их следования, называется транспонированной. Очевидно, что .

Главная диагональ квадратной матрицы – воображаемая прямая, проходящая через элементы с одинаковыми индексами из левого верхнего в правый нижний ее угол. Эти элементы – диагональные. Побочная диагональ – прямая, идущая из правого верхнего в нижний левый угол матрицы.

Квадратная матрица, у которой все элементы вне главной диагонали равны 0, называется диагональной. Среди диагональных элементов может быть и нулевые.

Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны 1, например: – единичная матрица третьего порядка.

Основные операции над матрицами

Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и все соответствующие их элементы совпадают.

Произведением матрицы А размером на действительное число называется матрица С размером , элементы которой равны .

Умножение матриц на число обладает следующими свойствами: .

Суммой двух матриц А и В размером называется матрица С, элементы которой равны .

Очевидно, что сложение матриц обладает следующими свойствами:

Произведением матрицы А на матрицу В называется матрица С, элементы которой равны сумме произведений элементов i строки матрицы А на соответствующие элементы j столбца В: .

Произведение матриц имеет смысл в том случае, если число столбцов матрицы А совпадает с числом строк матрицы В. В общем случае АВ ВА, т. е. произведение некоммутативно.

Свойства произведения матриц:

АЕ=ЕА=А (единичная матрица Е– как 1 при умножении чисел);
(АВ)С=А(ВС) – ассоциативно;
(А+В)С=АС+ВС дистрибутивный закон.

Пример 1.1 . Найти , . ;

Очевидно, что .

Алгебраические дополнения.

Минором любого элемента матрицы n-го порядка будем называть определитель порядка n–1, соответствующий матрице, которая получена из данной вычеркиванием строчки с номером i и столбца с номером j, на пересечении которых находится данный элемент. Минор элемента будем обозначать .

Алгебраическим дополнением элемента назовем число, равное .

Тогда сформулируем свойство 8 определителей:

8. Определитель равен сумме произведений элементов какой-нибудь строки (или столбца) на алгебраические дополнения этих элементов.

Последнее свойство определителей:

9. Сумма произведений элементов какой-либо строки на соответствующие алгебраические дополнения элементов другой строки равна нулю.

Ранг матрицы.

Пусть имеется прямоугольная матрица размером m на n: . Если в этой матрице выделить k строк и k столбцов, то мы получим квадратную матрицу порядка k. Определитель этой матрицы называется миноромk – го порядка матрицы А. Среди этих миноров найдется хотя бы один, отличный от нуля, минор старшего порядка. Порядок наибольшего минора, отличного от нуля, называется рангом матрицы r(A). Тот минор r-го порядка, который отличен от нуля, назовем базисным минором (у матрицы А может быть несколько миноров r-го порядка, которые отличены от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами.

Свойства ранга:

1. Ранг матрицы не меняется при ее транспонировании, т.к. строки и столбцы равноправны в отношении ранга.

2. Ранг матрицы не меняется при перестановке ее строк.

3. Ранг матрицы не меняется при умножении всех элементов какой-либо строки на отличное от нуля число.

4. Ранг матрицы не меняется, если к одной из ее строк прибавить другую строку, умноженную на некоторое число.

5. Ранг матрицы не меняется, если удалить нулевую строку.

6. Ранг матрицы не меняется, если удалить строку, являющейся линейной комбинацией другой строки.

Напомним, что элементарными называются следующие преобразования матриц:

· Перестановка двух любых строк и столбцов;

·Умножение строки или столбца на число отличное от нуля;

· Прибавление к одному столбцу или строке линейной комбинации других столбцов или строк.

Элементарное преобразование не меняет ранг матрицы (это следует из свойств).

Каноническойназывается матрица, у которой в начале главной диагонали стоит подряд несколько единиц, а все остальные элементы равны нулю.

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической.

Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Рассмотрим другой метод вычисления ранга матрицы, называемый методом окаймляющих миноров. В рассматриваемой матрице находим элемент, отличный от нуля, тогда ранг матрицы не меньше единицы. Затем выбираем минор второго порядка (определитель), отличный от нуля и содержащий выбранный ранее элемент. Если такой минор существует, то ранг матрицы не менее двух. Далее выбираем минор 3-его порядка, отличный от нуля, в который входит минор второго порядка. Если такой минор 3-его порядка существует, то ранг матрицы не менее трех, и т.д.

Обратная матрица.

Рассмотрим квадратную матрицу А порядка n: . Считаем, что матрица А – невырожденная, т.е. ее определитель отличен от нуля.

Квадратная матрица А^-1 называется обратной для матрицы А, если выполняются равенства:

А^-1А=АА^-1=Е, где Е – единичная матрица порядка n.

Теорема. Для того чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Доказательство.

1) Необходимость. Пусть матрица А имеет обратную матрицу, тогда будет выполняться равенство . Вычислим определитель от левой и правой части: det (А^–1А)=det E, , отсюда det A¹ 0.

2) Достаточность. Предположим, что определитель матрицы det А отличен от нуля. Рассмотрим матрицу . Это присоединенная матрица, в которой A_ij – алгебраическое дополнение элементов a_ij матрицы А, причем алгебраические дополнения образуют транспонированную матрицу. Рассмотрим произведение . В этом произведении любой элемент, не лежащий на главной диагонали, равен нулю, т.к. это сумма произведений элементов одной строки на алгебраические дополнения другой строки. Элементы, лежащие на главной диагонали, равны определителю матрицы det А:

Таким образом, Окончательно получим формулу для обратной матрицы: .

Полученная формула является достаточно громоздкой, поэтому рассмотрим другой способ определения обратной матрицы.

Элементарными называются следующие преобразования матриц:

· Перестановка двух любых строк и столбцов.

· Умножение строки или столбца на число отличное от нуля.

· Прибавление к одному столбцу или строке линейной комбинации других столбцов или строк.

Две матрицы называется эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Если матрицы А и В – эквивалентные, то это обозначают так: A≈ B.

Для отыскания обратной матрицы выполним элементарные преобразования следующей матрицы: , в левой части которой – матрица А, а в правой – единичная матрица. С помощью элементарных преобразований на месте матрицы А нужно получить единичную матрицу, тогда на месте единичной матрицы получится обратная матрица.

Пример 1.3. Вычислить обратную матрицу для матрицы

Определитель матрицы Алгебраические дополнения:

Тогда .

Метод Гаусса

Рассмотрим систему n линейных уравнений с n неизвестными (2.1). Метод Гаусса представляет собой систематизированную схему последовательного исключения неизвестных. Пусть (иначе переставим местами уравнения). С помощью первого уравнения исключим переменную х₁ из второго и последующих уравнений. Для этого от второго уравнения отнимем первое, умноженное на , от третьего – первое, умноженное на и т.д. Получим систему уравнений с новыми коэффициентами. Пусть , тогда аналогично исключим х₂ из третьего и последующих уравнений. Для этого умножим второе уравнение на и вычтем полученный результат из третьего, из четвертого уравнения вычтем второе, умноженное на и т.д. Продолжив дальнейшее исключение неизвестных, получим систему с так называемой треугольной матрицей:

Эта процедура называется прямым ходом метода Гаусса. Далее начинаем обратный ход метода Гаусса, т.е. нахождение неизвестных. Находим x_n из последнего уравнения, затем найденное значение x_n подставляем в предпоследнее уравнение и определяем x_n_–1. Найденные значения x_n и x_n_–1подставляем в (n – 2)-е уравнение и находим х_n–2. Продолжая этот процесс, определяем остальные неизвестные системы.

Мы полагали, что . Однако, при данных преобразованиях мы можем получить уравнения вида , в котором все коэффициенты при неизвестных равны 0. При этом возможны два случая.

Если а=0, то система имеет бесконечное количество решений. При этом одно (или несколько) уравнений являются следствием остальных.

Если , то система не имеет решений.

Как отыскивать решения системы в первом случае, будет указано в следующем пункте. При решении систем линейных уравнений методом Гаусса удобно приводить к треугольному (или ступенчатому) виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя все преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Пример 2.2. Решить систему из примера 2.1 методом Гаусса. Запишем расширенную матрицу системы: ~ . В результате прямого хода матрица системы приведена к треугольному виду и найдено, что . Получим единичную матрицу, т.е. накопим нули выше главной диагонали:

. Таким образом, .

Решение произвольных СЛАУ

Рассмотрим систему m линейных уравнений с n неизвестными:

Для решения произвольной системы алгебраических уравнений необходимо вычислить ранг матрицы системы r(А). Если он совпадает с рангом расширенной матрицы, то система имеет решение. Считаем, что базисный минор расположен в первых r строках и столбцах системы. Уравнения, соответствующие базисным строкам, назовем базисными уравнениями. Неизвестные, соответствующие базисным столбцам, назовем главными, а остальные – свободными. Система линейных уравнений эквивалентна системе своих базисных уравнений.

Если r = n, то система имеет единственное решение по теореме Кронекера–Капели. Если r < n, то перенесем в правую часть все члены, кроме тех, которые содержат r главных неизвестных. Свободным неизвестным придадим числовые значения . Тогда получившуюся систему r уравнений с r неизвестными решаем по формулам Крамера или методом Гаусса и находим: . Тогда вектор является решением базисной системы, а также решением исходной системы в силу их эквивалентности.

Если ранг системы r меньше числа неизвестных n, то система имеет бесконечно много решений, при этом r неизвестных (главных) линейно выражаются через (n-r) свободных неизвестных. Сформулируем правило решения произвольной системы.

1. Вычисляя ранги основной и расширенной матриц системы, выясняем вопрос о е совместности. Если система совместна, то находят какой-либо базисный минор порядка r.

2. Берется r уравнений, из коэффициентов которых составлен базисный минор, остальные уравнения отбрасывают. Неизвестные, коэффициенты которых входят в базисный минор, считают главными и оставляют слева, а остальные (n – r) – свободными и переносят в правую часть уравнений.

3. По формулам Крамера или методом Гаусса находим выражения главных неизвестных через свободные. Полученные равенства представляют собой общее решение системы.

4. Придавая свободным неизвестным любые числовые значения, определяют значения главных неизвестных и находят частные решения системы.

Если положить, что свободные неизвестные равны нулю, то мы получим базисное решение. Базисных решений обычно несколько. В общем случае их число равно – это число сочетаний из n элементов по r: .

Пример 2.3. Найти общее решение системы:

Запишем расширенную матрицу системы, методом Гаусса, исключим неизвестные:

. Ранг системы равен 2. Поскольку главный минор второго порядка отличен от нуля, выберем в качестве главных неизвестных и , а неизвестные и будем считать свободными. Запишем систему в виде: ; , преобразуем первое уравнение:

Тогда общее решение системы: .

Матричные уравнения

Дана система n линейных уравнений с n неизвестными (2.1). Введём обозначения:

, , , тогда данную систему можно записать в матричном виде . Умножим это уравнение на обратную матрицу А^-1слева(считаем, что определитель матрицы системы не равен 0). Тогда: ,

. Это формула для решения уравнения (2.1) с помощью обратной матрицы.

Если в уравнении все три матрицы являются квадратными, причем , тогда решение .

Рассмотрим матричное уравнение вида . Имеем ; .

Пример 2.4. Решить систему примера 2.1 матричным способом (способом обратной матрицы).

Матрица системы , матрица неизвестных , матрица свободных членов .

Найдем обратную матрицу . вычислим алгебраические дополнения: ; ; ; ; ; ; ; ; . Тогда решение системы определены по формуле :

, т.е. .

Пример 2.5. Решить уравнение . Пусть , , тогда Вычислим ; имеем: .

Глава 3. Векторы

Прямая в пространстве

В общем случае прямую в пространстве можно рассматривать как линию пересечения 2-х плоскостей:

Канонические уравнения прямой

Пусть (∙ ) М₀(x₀; y₀; z₀) – точка лежащая на прямой; , где m, n, p – координаты направляющего вектора прямой, т.е. вектора параллельного данной прямой. М (x; y; z) – текущая точка. , получаем уравнение – канонические уравнения прямой.

Чтобы перейти от общего уравнения прямой к каноническому, в качестве точки М₀берут любое решение системы, направляющий вектор прямой можно найти как векторное произведение векторов нормалей × .

. Если направляющий вектор прямой задан точками M₁, M₂, то можно записать уравнение прямой, проходящей через 2 данные точки , : .

Угол между прямыми

Пусть 2 прямые заданы в канонической форме, т.е. известны направляющие векторы каждой прямой: , .

Угол между прямыми равен углу между направляющими векторами: .

Если прямые параллельны, то и .

Если прямые перпендикулярны, , то =0 и = 0 – условия перпендикулярности прямых.

Окружность

Окружность- это геометрическое место точек, каждая из которых отстоит от центра (О) на одинаковом расстоянии r. Пусть (•) М (x; y) – текущая.

Центр окружности: (•) О (a, b).

Эллипс

Эллипс – это геометрическое место точек, для которых сумма расстояний от двух фиксированных точек, называемых фокусами, есть величина постоянная (большая расстояния между фокусами).

Пусть , тогда . ; . , , .

; ;

;

. Вводим , (a> c), ;

- каноническое уравнение эллипса.

Эллипс симметричен относительно осей OX и OY (x² и y²).

x=0, y=b: (•)B (0; b); y=0, x=a: (•)A (a; 0). A, B, A^*, B^*– вершины эллипса, О – центр эллипса. большая полуось, малая полуось.

Эксцентриситет – отношение расстояния между фокусами к длине его большой оси: ; ; . Для окружности a = b и ε = 0, чем больше ε, тем больше эллипс вытянут.

Параметрические уравнения эллипса: ; .

Эллипс получается при сечении цилиндра и проекция окружности на плоскость.

Гипербола

Гипербола – это геометрическое место точек, для которых разность расстояний от двух фиксированных точек, называемых фокусами, есть постоянная величина, взятая по модулю и меньше расстояния между фокусами.

F₁ и F₂-фокусы, F₁F₂=2c. Пусть (•) М (x; y)-текущая. или, 2a< 2c, т.о. a< c. ; ;

;

– каноническое уравнение гиперболы; ; x=0; , y=0, x=a – вершина. Прямые – асимптоты.

Прямые – асимптоты.

Эксцентриситет – отношение расстояния между фокусами гиперболы к расстоянию между ее вершинами, , характеризует форму гиперболы.

Гипербола может иметь уравнение , тогда ее график имеет вид:

Парабола

Парабола – геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки – фокуса равно расстоянию до некоторой фиксированной прямой, называемой директрисой (не проходит через фокус). Фокус F, расстояние от F до директрисы равно p – параметр параболы. Начало координат – посередине между F и директрисой.

, , .

Парабола симметрична относительно ОХ. х=0, у=0. (у²< 0), . Пусть х=1, тогда . Длина хорды параболы, проведенной перпендикулярно оси, равна . p характеризует «ширину» области, ограниченной параболой.

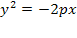
Полярное уравнение определяет эллипс , параболу и ветвь гиперболы .

p\2

Пример:

– гипербола с центром в точке C (2, –3)

Глава 5. Функции

Бесконечно малые величины

Функция называется бесконечно малой величиной при , если её предел равен 0, т.е. . Например, ; , если : .

Теорема. Если , то где – бесконечно малая при .

По условию . Это значит, что для любого , что для всех и удовлетворяющих верно . Обозначив , получим . Это означает, что – бесконечно малая при .

Обратная теорема. Если (бесконечно малой), то .

По условию . Т.к. - бесконечно малая при , то , что для всех и удовлетворяющих верно .

это означает, что .

Свойства бесконечно малых величин:

1. Сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на константу есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от 0, есть величина бесконечно малая.

Замечание. Пусть и две бесконечно малые величины. В этом случае их отношение называется неопределенностью и требует дальнейших вычислений.

Сравнение бесконечных малых.

Пусть имеется несколько бесконечно малых величин α (х), β (х), γ (х).

1. Если β /a имеет конечный и не равный нулю предел, т.е. lim β /α =A≠ 0 и lim α /β ≠ 0, то бесконечно малые β и α называются бесконечно малыми одного порядка малости.

Пример. 2, x и sin2x – бесконечно малые одного порядка.

2. Если β / α → 0, то есть lim β / α =0 (а lim α /β = ∞ ), то β называют бесконечно малой величиной высшего порядка малости, чем бесконечно малая α , α – бесконечно малая низшего порядка, чем β . Запись – есть 0 малое от .