
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Стохастический расчет временных характеристик проектов.
Метод PERT - time
На практике при формировании первичных сетевых моделей бывает очень сложно дать точную оценку длительности выполнения отдельных работ. Особенно если это работы творческие по содержанию, например; исследовательские, конструкторские и др. Тогда их продолжительности считаются случайными величинами и задаются с помощью системы оценок. Вспомним, что для задания случайной величины, как правило, достаточно указать: 1) закон ее распределения, 2) математическое ожидание, 3) дисперсию. Однозначного решения относительно закона распределения продолжительностей работ нет. Ученые склоняются к двум вариантам, которым соответствуют два подхода. 1. Если длительность работ считать подчиняющейся закону b-распре-деления, то следует использовать двухоценочную систему, в которой для каждой работы задаются: а ij - оптимистическая оценка длительности, bij - пессимистическая оценка длительности aij £ tij £ bij . и рассчитываются:
s2ij - дисперсия длительности, s2ij = 2. Если длительность работ считать подчиняющейся нормальному закону распределения, то следует использовать трехоценочную систему, в которой дополнительно задается третья оценка mij - медиана, а расчеты выполняются несколько иначе:
s2ij = Далее могут быть рассчитаны все временные характеристики проекта с помощью уже известных алгоритмов (см. разд. 3.5). Поскольку в алгоритмах используются только действия сложения и вычитания и применяются они к математическим ожиданиям длительностей работ, то и результат любого расчета также будет представлять собой математическое ожидание случайной величины. Ее дисперсия будет равна сумме дисперсий тех работ, что участвовали в расчете. Рассчитанные таким образом параметры проекта в силу центральной предельной теоремы теории вероятности распределены по нормальному закону. Всё сказанное справедливо лишь для достаточно больших проектов, где при расчетах параметров суммируются более десятка случайных величин – длительностей работ. Стохастическая постановка управления проектами позволяет решить две специфические задачи. Найти: 1) с какой вероятностью проект будет завершён к плановому сроку, 2) к какому сроку проект может быть завершён с заданной вероятностью. Для решения обеих задач используется x - нормированное отклонение случайной величины, распределенной нормально, или квантиль. Если задан плановый срок Тпл , то выполняется расчет x(р) = где s2кр - дисперсия критического пути, рассчитанная как сумма дисперсий работ, лежащих на критическом пути, s2кр = Затем по таблице накопленной (интегральной) вероятности для нормального закона (см. Приложение) отыскивается значение искомой вероятности. Если задана требуемая вероятность завершения проекта р0, то расчет ожидаемого срока выполняется по формуле Тож = Ткр + x(р0) sкр . При этом значение квантиля определяется на основании заданной вероятности по той же таблице. Она представляет собой основное поле, где приведены значения вероятности, и "рамку", в которой указаны значения квантиля: в крайнем левом столбце – целые и десятые доли, а в верхней строке – сотые доли. Функция накопленной вероятности симметрична относительно "0" для квантиля и "0,5" – для вероятности, поэтому в таблицу включена только одна ее "ветвь". Это означает, что в основном поле приведены только отклонения вероятности от 0,5, причем, если существует отклонение в большую сторону, то квантиль принимает положительное значение, если в меньшую – отрицательное. Так, например, квантиль вероятности 0,67 = (0,5 + 0,17) равен по модулю (0,44) квантилю вероятности 0,33 = (0,5 – 0,17), но имеет другой знак. Пример Пусть задана вероятностная сетевая модель проекта, топология которой показана на рис. 3.14, а оценки длительностей работ сведены в табл. 3.5. Использована трехоценочная система. Требуется определить, с какой вероятностью проект будет завершен к следующим срокам: а) Тпл = 160 дн., б) Тпл = 159 дн., в) Тпл = 155 дн.; а также, к какому сроку завершится проект со следующими вероятностями : а) р0 = 0,8, б) р0 = 0,5, в) р0 = 0,1.
10
Рис. 3.14. Исходная сетевая модель проекта для стохастического расчета Таблица 3.5
В табл. 3.5 показаны также результаты расчета математических ожиданий и дисперсий длительностей всех работ сети. Выделены дисперсии работ критического пути, в сумме составляющие s2кр = 8,44. Расчет ранних сроков событий, в том числе продолжительности критического пути, нахождение последовательности работ критического пути выполнены с помощью метода Форда (табл. 3.6). Таблица 3.6
111,33 | 59,17 | 68 92 131,5 | 70,33 | 76 149,17 | 159,33 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 85 | 85 | 111,33 | 59,17 | 131,5 | 70,33 | 149,17 | 159,33 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассчитаем значения квантиля для трех вариантов прямой задачи и найдем по ним вероятности, используя таблицу в Приложении:
а) Тпл = 160 дн.,
x(р) =  = 0,2305, Þ р = 0,5 + 0,0909 = 0,5909;
= 0,2305, Þ р = 0,5 + 0,0909 = 0,5909;
б) Тпл = 159 дн.,
x(р) = 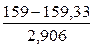 = - 0,1136, Þ р = 0,5 - 0,0457 = 0,4543;
= - 0,1136, Þ р = 0,5 - 0,0457 = 0,4543;
в) Тпл = 155 дн.,
x(р) =  = -1,4900, Þ р = 0,5 - 0,4319 = 0,0681.
= -1,4900, Þ р = 0,5 - 0,4319 = 0,0681.
Теперь, используя ту же таблицу, отыщем квантили по заданным значениям вероятности и на их основе рассчитаем ожидаемые сроки завершения проекта:
а) р0 =0,8 Þ x(р0 ) = 0,841,
Тож = 159,33 + 0,841´ 2,906 = 161,77 дн.;
б) р0 =0,5 Þ x(р0 ) = 0,
Тож = 159,33 + 0 ´ 2,906 = 159,33 дн.;
в) р0 =0,1 Þ x(р0 ) = - 1,281,
Тож = 159,33 - 1,281´ 2,906 = - 155,61 дн.
Логично было бы предполагать, что вероятность завершения проекта к сроку, превышающему математическое ожидание Ткр , окажется более 50 %, к сроку, меньшему, чем математическое ожидание Ткр , - менее 50 %, а с вероятностью 50 % проект завершится именно к этому сроку. Расчеты полностью подтверждают логику наших рассуждений.
Задачи для самоконтроля
1. Граф размерностью n = 9, k = 15 задан аналитически: {N} = 1, 2, 3, 4, 5, 6, 7, 8, 9; {A} = 1-5, 1-6, 1-7, 2-7, 2-8, 3-7, 4-3, 4-5, 4-7, 7-5, 8-3, 8-4, 8-9, 9-3, 9-4. Требуется составить для него матрицу смежности вершин, считая граф ориентированным, и изобразить его графически. Проверить граф на связность и наличие циклов.
2. Граф, заданный в предыдущей задаче, требуется упорядочить сначала методом вычеркивания, затем методом Де-Мукрона. Использовать при этом оба подхода: исключение предков и исключение потомков. Изобразить граф разбитым на слои. Сравнить полученные результаты.
3. На рис. 3.15 заданы графы.
 |  |  |




 а) А В Е
а) А В Е




 Д
Д




 Б Г Ж
Б Г Ж
 |  |  |







 б) Б Д К
б) Б Д К



 А
А



 Л
Л




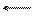
 В Г И
В Г И







 Е Ж З М
Е Ж З М
Рис. 3.15. Исходные графы для упорядочения к задаче 3
Требуется упорядочить их методом Де-Мукрона и изобразить разбитыми на слои. Вершины перенумеровать. Использовать оба способа: исключение предков и исключение потомков.
4. Предложите формальный способ проверки графа на наличие циклов и отыскания вершин, вошедших в цикл (циклы). Используйте для этого, например, матрицу смежности вершин графа.
5. Составьте сетевую модель в терминах "работы–связи" по информации из табл. 3.7. Представьте затем полученную сеть в терминах "события-операции".
Таблица 3.7
| Обозначение работы | Содержание работы | Обозначения предшествующих работ |
| а | Разработка проекта дома на садовом участке | - |
| б | Валка леса на участке | - |
| в | Корчевка пней на месте будущего дома | б |
| г | Корчевка пней на остальном пространстве участка | в |
| д | Рытье котлована под фундамент дома | а, в |
| е | Закупка материалов для строительства | а |
| ж | Завоз материалов на участок | е |
| з | Заливка фундамента | д, ж |
| и | Возведение дома | з |
| к | Внутренняя отделка дома | и |
| л | Перекопка земли на участке | г, и |
| м | Разработка плана посадок на участке | г, и |
| н | Закупка посадочного материала | м |
| о | Посадки | л, н |
| п | Рытье колодца | г, и |
| р | Празднование новоселья с друзьями | к, о, п |
6. Составьте сетевую модель комплекса работ, самостоятельно определив логику их следования:
Согласование технического задания на разработку прибора.
Разработка блок-схемы прибора.
Разработка принципиальной схемы блока А.
Разработка принципиальной схемы блока Б.
Разработка принципиальной схемы блока В.
Разработка принципиальной схемы блока Г.
Расчет на ПЭВМ схемы блока Г.
Составление единой принципиальной схемы прибора.
Заказ недостающих комплектующих изделий для изготовления прибора.
Разработка конструкции корпуса прибора.
Сборка макета прибора.
Испытания макета и доработка схемы прибора.
Изготовление корпуса прибора.
Сборка и монтаж прибора в корпусе.
Разработка эксплуатационной документации на прибор.
Сдача прибора заказчику.
7. На рис. 3.16 показаны фрагменты сетевых моделей в терминах "работы–связи". Требуется представить их в терминах "события–операции".














 а) А Б б) А В
а) А Б б) А В



 Г Б Г Е
Г Б Г Е



 В
В
Д Д
Рис. 3.16. Фрагменты сетевых моделей
в терминах «работы–связи»
8. На рис. 3.17 показана сетевая модель комплекса работ. Около работ проставлены продолжительности их выполнения. Требуется рассчитать ранние и поздние сроки свершения событий методом Форда (табличным), резервы событий, найти критический путь, рассчитать все параметры работ и свести их в таблицу.




 5 4
5 4




 8 3 9 5 15
8 3 9 5 15
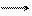


 1 1 6 7
1 1 6 7


 4 2 6 7
4 2 6 7
15
Рис. 3.17. Исходная сетевая модель для расчетов
9. Придумайте самостоятельно сетевую модель, отвечающую всем необходимым требованиям, с параметрами:
а) n = 6, k = 8;
б) n = 7, k = 11;
и задайте на ней продолжительности работ. Выполните расчеты всех временных характеристик; результаты сведите в таблицы. Найдите и укажите на сети критический путь.
10. На рис. 3.18 показана сетевая модель проекта, продолжительности выполнения работ которого - случайные величины, заданные трехоценочным способом в табл. 3.8.
Требуется определить, к какому сроку будет завершен проект с вероятностями: а) 35 %, б) 50 %, в) 84 %, г) 96,5 %; какова вероятность завершения проекта к срокам: а) 80,5; б) 79,0; в) 83,5.





 3 8
3 8







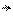








 1 2 5 6 10 12 13
1 2 5 6 10 12 13














 4 7 9 11 14
4 7 9 11 14

15
Рис. 3.18. Исходная сетевая модель для расчетов к задаче 10
Таблица 3.8
| Код работы | Оценки длительности работы | Код работы | Оценки длительности работы | ||||
| aij | mij | bij | aij | mij | bij | ||
| 1-2 | 1 | 2 | 6 | 7-9 | 3 | 5 | 7 |
| 1-4 | 1 | 2 | 3 | 9-11 | 10 | 18 | 20 |
| 2-3 | 8 | 10 | 12 | 10-12 | 4 | 6 | 9 |
| 2-5 | 3 | 4 | 9 | 11-12 | 6 | 8 | 10 |
| 4-6 | 4 | 5 | 8 | 11-14 | 2 | 3 | 4 |
| 4-7 | 4 | 5 | 8 | 11-15 | 19 | 21 | 23 |
| 5-6 | 1 | 2 | 5 | 12-13 | 3 | 5 | 9 |
| 6-8 | 4 | 7 | 9 | 12-14 | 1 | 2 | 3 |
| 6-9 | 15 | 21 | 24 | 13-14 | 5 | 6 | 9 |
| 6-10 | 6 | 10 | 14 | 14-15 | 8 | 10 | 12 |
11. Придумайте самостоятельно стохастическую сетевую модель, отвечающую всем необходимым требованиям, с параметрами:
а) n = 16, k = 25;
б) n = 18, k = 28
и задайте оценки продолжительностей работ. Выполните расчет ранних сроков. Найдите и укажите на сети критический путь. Определите, к какому сроку проект будет завершен с вероятностью: а) 5 %, б) 67 %, с) 98 %. Задайте плановый срок и определите вероятность, с которой проект будет завершен к этому сроку.
Тема 4. ПОТОКИ В СЕТЯХ.
Последнее изменение этой страницы: 2019-03-31; Просмотров: 576; Нарушение авторского права страницы