Эквивалентность автоматов

ПРОЕКТИРОВАНИЕ АВТОМАТОВ

 

Федеральное агентство по образованию

ГОУ ВПО «Уральский государственный технический университет -УПИ»

 

В.П.Битюцкий

И.В.Хмелевский

 

ПРОЕКТИРОВАНИЕ АВТОМАТОВ

Учебное пособие

 

Научный редактор– проф., д-р техн.наук В.И.Кузякин

 

 

 

 

 

Екатеринбург

2006

 

 

УДК 519.713.001.63

ББК 32.815-02

Б66

 

Р е ц е н з е н т ы

Кафедра информатики Уральского  государственного горного университета (зав.кафедрой проф., д-р техн. наук М.Б.Носырев);

доц., канд.техн.наук Г.Б.Захарова (УрО РАН).

 

 

Авторы: В. П. Битюцкий И.В.Хмелевский

Б66 Проектирование автоматов: учебное пособие /В.П. Битюцкий, И.В.Хмелевский. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 93 с.

ISBN 5-318-00537-3

 

 

Приводятся основные понятия и утверждения из теории абстрактных и структурных автоматов, вопросы их минимизации, композиции, декомпозиции и синтеза. Решение задачи проектирования автоматов доведено до синтеза схемы автомата в заданном базисе.

 Рассмотрены вопросы учёта временных характеристик элементов, гонки и состязания в сетях, способы противогоночного кодирования состояний автомата.

Отдельный раздел посвящен автоматам-распознавателям, для чего рассмотрены формальные грамматики и языки, которые понимают автоматы.

 

 

Библиогр. : 5 назв. Табл. 50. Рис. 32.    

 

УДК 519.713.001.63

ББК 32.815-02

 

 

ISBN 5-318-00537-3                ÓГОУ ВПО «Уральский государственный

технический университет-УПИ»,   2006

Ó В.П. Битюцкий, И.В.Хмелевский 2006

 

Оглавление

Введение. 5

1. Абстрактные автоматы.. 7

1.1. Эквивалентность автоматов. 9

1.2. Минимизация автоматов. 13

1.2.1. Минимизация полностью определенного автомата. 13

1.2.2. Минимизация частичного автомата. 14

1.3. Композиция автоматов. 20

1.3.1. Параллельное соединение. 20

1.3.2. Последовательное соединение. 20

1.3.3. Соединение с обратной связью.. 21

1.3.4. Соединение в сеть. 21

1.4 Декомпозиция автомата. 24

1.4.1. Задача декомпозиции. 24

1.4.2. Разбиения со свойствами подстановки. 25

1.4.3. Метод декомпозиции. 27

1.5. Упражнения. 31

Эквивалентность автоматов. 31

Минимизация полностью определённого автомата. 33

Декомпозиция автоматов. 34

2. Структурные автоматы.. 37

2.1. Автоматная полнота и теорема В.М.Глушкова. 37

2.2. Гонки в автомате. 40

2.2.1. Кодирование состояний. 40

2.2.2. Понятие о гонках. Противогоночное кодирование. 40

2.3. Проектирование автомата. 42

2.4. Упражнение. 46

Кодирование. 46

Синтез автомата. 48

3. Синтез схем.. 49

3.1. Определения. 49

3.2. Функциональная полнота базиса. 50

3.2.1. Классы функций. 50

3.2.2. Монотонные функции. 50

3.2.3. Самодвойственные функции. 51

3.2.4. Линейные функции. 52

3.2.5. Функции, сохраняющие константу. 53

3.2.6. Функциональная полнота. 54

3.3. Топологические ограничения в схемах. 56

3.3.1. Плоские схемы.. 57

3.3.2. Ограничения на глубину связи в схеме. 58

3.4. Методы синтеза схем.. 62

3.4.1. Метод факторизации. 62

3.4.2. Метод декомпозиции. 62

3.4.3. Синтез схем в классическом базисе. 65

3.4.4. Синтез схем в монофункциональном базисе. 65

3.5. Упражнения. 67

Функциональная полнота. 67

Синтез схем.. 67

4. Эксперименты над автоматами. 69

4.1. Построение диагностических деревьев. 69

4.2. Диагностические и установочные эксперименты.. 70

4.2.1. Дерево преемников. 71

4.2.2. Диагностический эксперимент. 72

4.2.3. Установочный эксперимент. 76

4.3. Упражнения. 76

Диагностические эксперименты.. 76

Установочные эксперименты.. 78

5. Формальные грамматики. 78

5.1. Языки и порождающие их грамматики. 78

5.2. Примеры фрагментов описаний в языках программирования. 82

5.3. Порождающая грамматика. 83

5.4. Классы языков и грамматик. 87

5.5. Язык, понимаемый устройством.. 87

5.6. Автоматные языки. 88

5.7. Упражнения. 92

Библиографический список. 92

 

 

Введение

Теория автоматов посвящена представлению преобразователей информации и связана с проектированием сложных вычислительных и управляющих систем. Глушков В. М. и Уитни У. высказали идею о том, что любую систему, поведение которой описывается алгоритмически, можно представить композицией управляющего и операционного уст-ройств. Первое из них является логически более сложным и для него используется автоматная модель (модель Мура-Миля). Примером может служить описание некоторой команды ЭВМ. Команда описывается алго-ритмом, элементарными операциями для которого служат операции над регистром (сдвиги, инвертирование), сумматором и другие. Алгоритму сопоставляется автомат управления выполнением команды. Этот автомат определяет порядок выполнения (инициализации) элемен-тарных операций. Регистры, сумматоры и другие образуют операционное устройство, в котором и выполняются элементарные операции.

Изучение автоматных моделей связано с реализацией (проектиро-ванием) и моделированием управляющих устройств в заданных базисах.

Второй областью, где используются автоматные модели, являются формальные языки. В частности, можно назвать проблему грамматиче-ского разбора фраз формального языка и проблему проверки правиль-ности конструкций языка. Здесь наиболее эффективный способ решения связан с использованием автоматных моделей.

Учебное пособие состоит из двух неравнозначных по объёму частей. В первой, включающей главы с 1-й по 4-ю, решаются вопросы проектирования автоматов-преобразователей. Подробно рассматрив-аются автоматы на абстрактном уровне, их минимизация, декомпозиция на связанные сетью более простые автоматы, переход к структурному автомату и его синтез. Решение задачи доведено до построения схемы из заданных элементов базиса.

Отдельными разделами в этой части стоят вопросы обеспечения корректной работы автомата при учёте разбросов временных характеристик элементов базиса – противогоночное кодирование автомата и эксперименты над автоматами.

Во второй части (глава 5) изучаются автоматы – распознаватели, которые предназначены для анализа формальных языков. Для этого приведены необходимые понятия из формальных языков и грамматик.

Изложение сопровождается поясняющими примерами и задачами, решение которых поможет более глубокому пониманию материала.

 

 

В стандарте специальности ВМКСС задачи профессиональной деятельности определены следующим образом:

инженер должен быть подготовлен к решению следующих профессиональных задач:

· определение целей проектирования объектов профессиональной деятельности, критериев эффективности проектных решений, ограничений;

· проектирование архитектуры аппаратно-программных комплексов и их компонентов;

· выбор средств вычислительной техники (ВТ), средств программирования и их применения для эффективной реализации аппаратно-программных комплексов;

· оценка надежности и качества функционирования объекта проектирования.

 Квалификационные требования.

Подготовка выпускника должна обеспечивать квалификационные умения для решения профессиональных задач:

· участие во всех фазах проектирования, разработки, изготовления и сопровождения объектов профессиональной деятельности;

· участие в разработке всех видов документации на программные, аппаратные и программно-аппаратные комплексы;

· использование современных методов, средств и технологии разработки объектов профессиональной деятельности.

Материал данного учебника должен стать базой для решения этих задач.

 

Абстрактные автоматы

Определение. Абстрактным автоматом Мили называется преобразователь, представимый пятёркой

S=<Z, W, A, l, d>,

где Z – входной алфавит {z1, z2, …, zr},

W – выходной алфавит {w1, w2,…, wp},

A  – алфавит состояний {a1, a2,…, at},

d– функция переходов AxZ® А,

l – функция выходов AxZ® W.

Если, кроме того, определено начальное состояние автомата a₀
(a₀ – символ из А), то говорят об инициальном  автомате Мили.

Семантика: автомат функционирует в дискретном времени. В лю-бой момент времени он находится в некотором состоянии a_i из множест-ва A, и на его вход поступает входной сигнал z_i из множества Z. В зави-симости от состояния и входного сигнала в следующий момент автомат переходит в новое состояние a_j, определяемое функцией перехода, a_j=d(a_i, z_i), при этом на его выходе формируется выходной сигнал
w=l(a_i, z_i) (рис.1.1). В инициальном автомате в начале функционирова-ния автомат находится в состоянии a₀ .

Автомат Мили представляется матрицей переходов и матрицей выходов, описывающими соответствующие функции.

Пример 1. Автомат задан на множествах входов Z={z1, z2, z3}, состояний A={a1, a2, a3, a4, a5, a6} и выходов W={w1, w2}. Его функционирование описывается матрицами переходов и выходов, приведёнными в табл.1.1 и 1.2.

 

Таблица 1.1

Таблица 1.2

a1

a2

a3

a4

a5

a6

a1

a2

a3

a4

a5

a6

z1

a3

a5

a6

a6

a1

a5

z1

w1

w1

w2

w1

w2

w1

z2

a1

a6

a4

a4

a4

a1

z2

w1

w1

w1

w1

w1

w1

z3

a5

a1

a3

a2

a5

a3

z3

w1

w1

w2

w2

w2

w1

Автомат Мили может быть также представлен в виде объединённой матрицы. В этом случае каждая клетка матрицы состоит из двух частей, в одной из которых записывается следующее состояние (функция d (ai, z)), во второй части – выход (функция l (ai, z)).

Таблица 1.3
	a1	a2	a3	a4	a5	a6
z1	a3w1	a5w1	a6w2	a6w1	a1w2	a5w1
z2	a1w1	a6w1	a4w1	a4w1	a4w1	a1w1
z3	a5w1	a1w1	a3w2	a2w2	a5w2	a3w1

Объединённая матрица представленного выше автомата показана в табл. 1.3.

Автомат Мили может быть описан в виде графа. Вершинам этого графа сопоставлены состояния, дугам – переходы. При этом на каждой дуге записывается значение входа, определяющего этот переход, и значение выхода на этом переходе. Эта пара вход-выход называется весом дуги. Для рассмотренного автомата граф имеет вид как на рис.1.2

 

 

Рис.1.2

Автоматом Мура называют автомат, в котором функция выходов зависит только от состояния, то есть для него функция выходов автомата: m: A®W.

Пример 2. Автомат Мура задан на тех же множествах, что и автомат в примере 1, а его функционирование описывает табл. 1.4.

В графе автомата Мура дуги взвешиваются только значением соответствующего входа, значение выходов приписываются его вершинам.

Таблица 1.4
	w a1	w1 a2	w2 a3	w1 a4	w2 a5	w1 a6
z1	a3	a5	a6	a6	a1	a5
z2	a1	a6	a4	a4	a4	a1
z3	a5	a1	a3	a2	a5	a3

Для приведённого автомата граф будет иметь вид как на рис.1.3

 

Рис.1.3

 

Реакция автомата в состоянии ai на входное слово z* определяется по таблицам переходов и выходов. Для последнего примера реакцией автомата в состоянии a2 на слово z1z2z1 будет слово w2w1w1.

 

Эквивалентность автоматов

 

Состояния автомата ai и aj называются эквивалентными, что обозначается как ai~aj, если для них имеет место: "z

1. l (ai, z)= l (aj, z),

2. d (ai, z)~ d(aj, z).

Свойства отношения эквивалентности состояний:

1. a_m ~ a_m, 2. a_m ~ a_n => a_n ~ a_m, 3. (a_m ~ a_k)&(a_n ~ a_k)Þ a_m ~ a_n.

Таким образом, это есть отношение эквивалентности в общепринятом теоретико-множественном смысле, и множество состояний разбивается на непересекающиеся классы состояний – классы эквивалентности.

Автоматы S=<Z, W, A, l, d>, и S1=<Z, W, A1, l1, d1>, называют эквивалентными, что обозначается как S ~S1, если ("аÎА $а1ÎА1, a ~ a1) &("а1ÎА1 $ аÎА, a1 ~ a).

 

Были введены две модели автоматов – автомат Мура и автомат Мили. Следующая теорема показывает, что эти модели равномощны, т.е. любой автомат можно реализовать в каждой из этих моделей.

Теорема.  Для любого автомата Мура существует эквивалентный ему автомат Мили и наоборот.

Доказательство теоремы построим на преобразовании автомата одного типа, описанного с помощью графа, в автомат другого типа.

Необходимость. Покажем, как для любого автомата Мура построить эквивалентный ему автомат Мили. Для этого достаточно перенести выходы автомата с вершин графа на входящие дуги графа.

Рассмотрим это на примере автомата Мура Sµ=<Z,W,A, l, d ,>, где А={a0, a1, a2, a3, a4}; Z={x1,x2,x3}; W={w1,w2}. Функции автомата представлены в виде графа на рис. 1.4. Результирующий автомат функционирует в соответствии с графом на рис.1.5. Полученный автомат эквивалентен исходному автомату по построению.

Достаточность. Покажем, что для любого автомата Мили можно построить эквивалентный ему автомат Мура. Для каждой вершины графа рассмотрим заходящие в неё дуги. Если эти дуги взвешены различными значениями выхода, то расщепим вершину таким образом, чтобы каждому значению выхода соответствовала своя вершина, и каждую дугу направим в свою вершину.

Пусть автомат Мили  S описан в виде графа на рис. 1.6. Рассмот-рим состояние a2, в которое заходят дуга (a0, a2), отмеченная выходом w1, и дуга (a3, a2), отмеченная выходом w3, и дуга (a1,a2), отмеченная выходом w2. Других заходящих дуг в эту вершину нет, значит расщепим вершину a2 в графе для автомата Мура на a2, которой сопоставим вы-ход w2 и куда направим дугу (a1, a2), вершину a1`, которой сопоставим

 

 

z2/w2

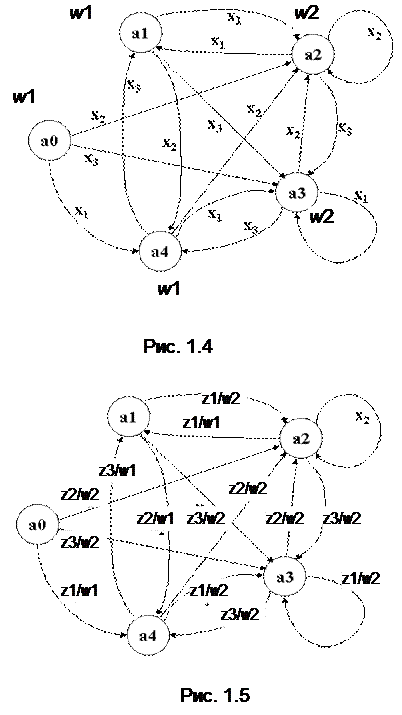
выход w1 и куда направим дугу (a0,a2`), и вершину a2``, куда направим дугу (a3,a2) и которой сопоставим выход w3. Выходные дуги для вновь введённых вершин будут те же, что и для исходной вершины. Таким образом, из вершин a2` и a2`` должны исходить дуги к тем же вершинам, что и из вершины  a2. 

Полученный автомат описан графом на рис. 1.7.     

 

	z2/w2

 

 

		Рис.1.6
			Рис.1.7

 

Очевидно, что автоматы S и S' эквивалентны по построению.

Модель автомата Мура проще, за простоту модели заплатили большим числом состояний.

Минимизация автоматов

 

Если состояния автомата эквивалентны, то они неразличимы между собой по реакции на любое входное слово. Автомат называется минимальным, если в нём нет эквивалентных состояний.

В предыдущем разделе введено понятие эквивалентности автоматов, позволяющее дать второе определение минимального автомата. Для автомата S минимальным автоматом называют автомат, имеющий минимальное число состояний среди множества автоматов, эквивалентных ему.

Задачу нахождения автомата, минимального заданному, называют задачей минимизации автомата.

 

Композиция автоматов

 

Рассмотрим основные виды соединений автоматов: параллельное, последовательное, с обратной связью и соединение в сеть.

 

Параллельное соединение

 

Параллельное соединение двух автоматов иллюстрируется на

следующем рисунке:

 

Здесь S1 = < Z1, W1, A1, l1, d1 > и S2 =< Z2, W2, A2, l2, d2 >.

Результирующим автоматом параллельного соединения двух автоматов S1 и S2 назовем автомат S = < Z, W, A, ll, d >, у которого:

Z = Z1 = Z2,

W = F(W1,W2 ),

A = A1 x A2, и для любого ab, где aÎA, bÎB имеет место

l(ab,z) = f(l1 (a,z), l2(b,z)),

d(ab,Z) = d1(a,z), d2(b,z).

 

 

Последовательное соединение

 

S1=<Z1,W1,A1 l1,d1>, S2=<Z2,W2,A2,l2,d2>

 

 

Результирующим автоматом последовательного соединения двух автоматов S1 и S2 (рис.1.9) назовем автомат S = <Z, W, A, l, d>, у которого:

Z  =  Z1;

W = W2;

W1= Z2;

A = A1 x A2;
и для любого ab, где aÎA, bÎB имеет место

l (ab,z) = l 2(b, l1(a,z));

d(ab,z) = (d1(a,z), d2(b, l1(a,z))).

 

Соединение в сеть

Определение

Компонентным автоматом (полуавтоматом Мура) называют автомат Мура, в котором каждому состоянию поставлен в соответствие свой выходной сигнал, отличный от выходных сигналов других состояний.

Говорят, что в таких автоматах обеспечена полнота выходов.

Определение.

Сетью автоматов назовем шестерку N = <Z,W,{Si},{fi},{wi},g> (i = 1...n),
где : Z - множество входов сети, W - множество выходов сети, Si - компонентный автомат сети с алфавитом входов Zi и алфавитом выходов Ai. Алфавит Zi = Z'I x Z''i поясняется рис. 1.11.

 

 

,

 

 

fi : A1 x...x An -> Zi'',      wi : Z -> Zi',    ,
n - количество компонентных автоматов.

 

Выходная функция g определяет выход сети.  g: A1 x...x An x Z -> W (рис.1.12).

Множество Si составляeт базис сети, множество {fi} определяeт её структуру.

 

Пример. Рассмотрим сеть, показанную на рис. 1.13.

1-я компонента:

w1   Z1 x1 Z2 x1 Z3 x2 Z4 x3

d1 b1 b2 b3 x1 b1 b1 b3 x2 b3 b2 b3 x3 b3 b2 b1

 

2-я компонента:

w2   Z1 y1 Z2 y2 Z3 y1 Z4 y2

f2 d1 d2 b1 q1 q2 b2 q1 q1 b3 q1 q1

d2 c1 c2 q1y1 c1 c1 q1y2 c2 c1 q2y1 c1 c2 q2y2 c2 c2

3-я компонента:

w3   Z1 t1 Z2 t2 Z3 t1 Z4 t2

f3   c1 p1 c2 p2

d3 d1 d2 p1t1 d2 d1 p1t2 d1 d2 p2t1 d1 d2 p2t2 d1 d1

Выход:

g	d1	d2
c1	w1	w2
c2	w1	w1

Сеть реализует автомат (результирующий автомат сети), состояния которого определяются как A1xA2X¼An.

Для приведённого примера автомат имеет 3 * 2 * 2 = 12 состояний. Введенные понятия сети автоматов и ее результирующего автомата позволяют сформулировать задачу композиции автоматов – для заданной сети описать автомат, реализуемый сетью.

Декомпозиция автомата

 

Задача декомпозиции

 

В разделе 1.2.2. для автомата S1 введено понятие реализующий (покрывающий) автомат S.

Задача декомпозиции – задача построения сети автоматов N, реализующей заданный автомат. Таким образом, задача декомпозиции состоит в том, чтобы для заданного автомата построить сеть из более простых автоматов, которая бы реализовала заданный автомат.

При декомпозиции используется аппарат разбиения множества состояний. Дадим необходимые определения.

Пусть множество А = {1 , 2 , 3 , 4 , 5 , 6}.

Разбиением p множества А называют множество его подмножеств, которые не пересекаются между собой и в объединении дают множество A. Эти подмножества называют блоками разбиения.

Например, для заданного множества разбиением может быть

p1(А) = {1234 , 56}.

Назовем одноэлементным разбиением множества А p₀(А) такое разбиение, в котором в каждом блоке содержится только один элемент множества А.

p0(А) = {1 , 2 , 3 , 4 , 5 , 6}.

Будем говорить, что разбиение p_i£p_j, если каждый блок разбиения p_i входит в какой-нибудь блок разбиения p_j.

Рассмотрим пример. Пусть p1(А) = {1234 , 56}, p2(А) = {12 , 34 , 56},

p₁(А) ³ p₂(А) ³ p₀(А).

p3(А) = {15 , 34 , 26},

p₁(А) и p₃(А) – не сравнимы.

Произведением разбиений p_i(А) и p_j(А) назовем разбиение p_k(А), которое содержит все непустые пересечения блоков разбиений-сомножителей.

Пример

p1(А) = {1234 , 56}, p2(А) = {1256 , 56},

p1(А) x p2(А) = {12 , 34 , 56}.

Множество разбиений p1(А), p2(А), …, pN(А) называется ортогональным, если произведение всех разбиений равно одноэлементному разбиению множества А.

p₁(А) x p₂(А) x … x p_N(А) = p₀(А)

Пример. p1(А)={1234, 56}, p2(А) = {1256, 34}, p3(А)={135, 246}.

p1(А) x p2(А) x p3(А) = {1 , 2 , 3 , 4 , 5 , 6} = p0(А)

Семантика. Составим каждому разбиению компонентный автомат. Будем считать, что в один блок включены все состояния исходного автомата, в которых данный компонентный автомат находится в состоянии, соответствующем блоку.

Общая теорема декомпозиции: Множеству разбиений {pi(А), i=1,N} можно сопоставить абстрактную сеть автоматов, реализующих заданный автомат S, тогда и только тогда, когда П pi(А) = p0(А).

 

Метод декомпозиции

Рассмотрим метод на примере автомата, представленного в табл.1.22. Алфавит состояний А = {1, 2, 3, 4, 5, 6},

алфавит входов Z = { z₁ , z₂ , z₃ , z₄ },

алфавит выходов W = {w₁ , w₂ , w₃}.

Нетрудно убедиться, что для этого автомата СП-разбиения нет.

 

Таблица 1.22
d/l	1	2	3	4	5	6
z1	2 / w1	5 / w1	1 / w1	6 / w1	1 / w3	2 / w2
z2	6 / w2	1 / w1	5 / w3	2 / w2	1 / w1	6 / w2
z3	6 / w1	1 / w1	5 / w1	2 / w2	2 / w3	5 / w3
z4	2 / w3	5 / w3	1 / w1	6 / w3	4 / w1	3 / w1

 

Выберем разбиения множества состояний А:
p1(А)={1234, 56}, p2(А) = {1256, 34}, p3(А)={135, 246}, т.е. сеть будет состоять из трёх компонентных автоматов. Условие теоремы выполняется, p₁(А), p₂(А) и p₃(А) – ортогональны.

Будем считать для выбранного примера, что алфавиты состояний компонентных автоматов A, B и С.

p1(А) = { 1234 , 56} = { b1 , b2} = B.

p2(А) = {1256 , 34} = {c1 , c2} = C.

p3(А) = {135 , 246} = {d1 , d2} = D.

Так, например, если автомат В (соответствующий разбиению p1(А)) находится в состоянии b1, автомат С (соответствующий разбиению p2(А)) – в состоянии с2, автомат D (соответствующий разбиению p2(А)) – в состоянии d1, то автомат SN будет находиться в состоянии 3. Выбор разбиений p1, p2, p3 определяет сложность функций fi, а от нее – со сколькими автоматами связан автомат S_i.

Для каждого разбиения pi построим функцию Fi: AxZ®pI на базе функции d. Эта функция определяет реакции автоматов Si на внешнее воздействие z i, при условии, что автомат S (и реализующий его автомат SN) находится в состоянии k.

Таблица 1.23
F1	1	2	3	4	5	6
z1	b1	b2	b1	b2	b1	b1
z2	b2	b1	b2	b1	b1	b2
z3	b2	b1	b2	b1	b1	b2
z4	b1	b2	b1	b2	b1	b1

Определим для функций F_i разбиения t_i на множестве А так, чтобы для любых а_k и а_m из множества А условие:

"ZÎZ Fi (ak, z)=Fi (am , z) выполнялось тогда и только тогда, когда ak и am принадлежат к одной группе разбиения ti. (табл.1.23 -1.25).

t1 = {136 , 24 , 5} , t2 = {1234 , 56}, t₃ = {14 , 23 , 5, 6},

Таблица 1.24
F2	1	2	3	4	5	6
Z1	c1	cl	cl	cl	cl	cl
Z2	cl	cl	cl	cl	cl	cl
Z3	cl	cl	cl	cl	cl	cl
Z4	cl	cl	cl	cl	c2	c2

Таблица 1.25
F3	1	2	3	4	5	6
Z1	d2	dl	dl	d2	dl	d2
Z2	d2	dl	dl	d2	dl	d2
Z3	d2	dl	dl	d2	d2	dl
Z4	d2	dl	dl	d2	d2	dl

 

Определим для функции F_i разбиения h_i на множестве Z так, чтобы для любых Z_k и Z_m из множества Z условие: "aÎA F_i (a, Z_k) = F_i(a , Z_m) выполнялось тогда и только тогда, когда Z_k и Z_m принадлежат к одной группе разбиения h_i.

h₁ = {z₁ z₄ , z₂ z₃} h₂ = {z₁ z₂ z₃ , z₄};

h₃ = {z₁ z₂ , z₃ z₄}.

Построим сеть N = < Z_N , W_N , {S_i} , {f_i} , {j_i} , g > Z_N = Z, W_N = W.

2) S_i , f_i , j_i - определяют компонентные автоматы;

S_i = ( A_i , Z_i , d_i ); A_i = { p_i } – блоки разбиения; 

 Z_i = Z_i` x Z<sub>i</sub>``, если Z<sub>i</sub>` не пустое множество,

Z_i = Z_i``, если Z<sub>i</sub>` пустое множество, Z<sub>i</sub>`` = h_i.

Z_i` определяются по следующему правилу:

Если p_ix(p_k x p_l x…xp_m)£t_i, то Z_i` = (p_k x p_l x … x p_m).

Найдём все возможные произведения пересечений.

p1(A)xp2(A) = {12, 56, 34}

p1(A) x p3(A) = { 13 , 5 , 24 , 6 } 

 p2(A) x p3(A) = { 15 , 26 , 3 , 4 }

p1(A) x p2(A) x p3(A)={ 1 , 2 , 3 , 4 , 5 , 6 }

Определим зависимость функции переходов первого автомата от других автоматов.

Таблица 1.26
d1	b1	b2
d1,u1	b1	b1
d1,u2	b2	b1
d2,u1	b2	b1
d2,u2	b1	b2

t1 > p1(A) x p3(A), => Z1` = p3(A) = {135, 246} = { d1 , d2} = D. Первый автомат зависит от третьего.

h₁ = {z₁ z₄ , z₂ z₃} = {u1 , u2} = U.

d₁: B x ( D x U ) ® B Функция переходов представлена в табл.1.26, композиция –
на рис.1.14

Определим зависимость функции переходов второго автомата от других автоматов

p2(A) x p1(A) ={13 , 5 , 24 , 6 }

t2 > p2(A) x p1(A), => Z2`=p1(A)={1234 ,56 }={b1, b2} = B,

h₂ ={Z₁, Z₂, Z₃, Z₄}={v1, v2}=V,

Таблица 1.27
d2	с1	с2
b1,v1	с1	с1
b1,v2	с1	с1
b2,v1	с1	*
b2,v2	c2	*

d₂:Bx(BxV)®C. Функция переходов представлена в табл.1.27, композиция – на рис.1.15

Определим зависимость функции переходов второго автомата от других автоматов

t3 = { 14 , 23 , 5 , 6 }

p1(A) x p2(A) x p3(A) = { 1, 2, 3, 4, 5, 6}.

t3 > p3(A) x p1(A) x p2(A)=> Z3`=p1(A)xp2(A)={12, 56, 34}={p1, p2, p3} = P,

h₃ = { Z₁ Z₂ , Z₃ Z₄ } = { v1 , v2 } = V,

d₃: D x ( P x V) ® D

 

Таблица 1.28
d3		d1	d2
p1,v1	b1,c1,v1	d2	d1
p1,v2	b1,c1,v2	d2	d1
p2,v1	b2,c1,v1	d1	d2
p2,v2	b2,c1,v2	d1	d2
p3,v1	b1,c2,v1	d1	d2
p3,v2	b1,c2,v2	d2	d1

Функция d₃ имеет вид, показанный в табл. 1.28.

Функция переходов представлена в табл.1.28, композиция –на рис.1.16.

 

 

Создадим разбиение множества P x V:

Q = { (p1,v1) (p1,v2) (p3,v2) , (p2,v1) (p2,v2) ( p3,v1) } = {q1, q2}.

Тогда функция d₃ принимает вид, показанный в табл.1.29.

 

Таблица 1.29
d3	d1	d2
q1	d2	d1
q2	d1	d2

 

 

Выходная функция представлена в табл.1.30, композиция –на рис.1.17.

 

 

Таблица1.30
g	b1,c1,d1	b1,c1,d2	b1,c2,d1	b1,c2,d2	b2,c1,d1	b2,c1,d2
	1	2	3	4	5	6
z1	w1	w1	w1	w1	w3	w2
z2	w2	w1	w3	w2	w1	w2
z3	w1	w1	w1	w2	w3	w3
z4	w3	w3	w1	w3	w1	w1

 

Упражнения

 

Эквивалентность автоматов

 

Для автомата Мили постройте эквивалентный ему автомат Мура.

Для полученного автомата Мура постройте эквивалентный ему автомат Мили и проведите его минимизацию через выделение
к-эквивалентных состояний.

 

Вариант 1

	1	2	3	4	5
z1	1/w1	3/w1	3/w1	2/w2	5/w1
z2	3/w2	1/w1	2/w1	3/w1	1/w2
z3	1/w2	4/w2	4/w2	5/w2	2/w1

 

Вариант 2

	1	2	3	4	5
z1	3/w1	1/w1	1/w1	2/w2	5/w1
z2	1/w2	3/w1	2/w1	1/w1	3/w2
z3	3/w2	4/w2	4/w2	5/w2	2/w1

 

Вариант 3

	1	2	3	4	5
z1	1/w1	3/w1	3/w1	2/w2	3/w1
z2	5/w2	1/w1	2/w1	5/w1	1/w2
z3	1/w2	4/w2	4/w2	3/w2	2/w1

 

Вариант 4

	1	2	3	4	5
z1	4/w2	2/w1	5/w1	5/w1	5/w1
z2	3/w1	1/w1	2/w1	3/w1	1/w2
z3	1/w2	4/w2	1/w2	5/w2	2/w1

 

Вариант 5

	1	2	3	4	5
z1	1/w1	3/w1	3/w1	2/w2	5/w1
z2	3/w2	1/w1	2/w1	3/w1	1/w2
z3	1/w2	4/w2	4/w2	5/w2	2/w1

 

 

Вариант 6

 

	1	2	3	4	5
z1	1/w1	2/w2	5/w1	1/w1	3/w1
z2	2/w1	1/w1	3/w2	5/w2	1/w1
z3	4/w2	5/w2	2/w1	1/w2	3/w2

 

 Вариант 7

	1	2	3	4	5
z1	3/w1	1/w1	1/w1	2/w2	5/w1
z2	4/w2	1/w1	2/w1	3/w1	1/w2
z3	3/w2	4/w2	4/w2	5/w2	2/w1

 

 Вариант 8

	1	2	3	4	5
z1	5/w1	5/w1	5/w1	2/w2	3/w1
z2	2/w1	3/w1	1/w2	5/w1	1/w2
z3	1/w2	5/w2	2/w1	3/w2	2/w1

 

 Вариант 9

	1	2	3	4	5
z1	1/w1	2/w2	5/w1	5/w1	5/w1
z2	2/w1	3/w1	1/w2	3/w1	1/w2
z3	4/w2	5/w2	2/w1	5/w2	2/w1

 

Вариант 10

	1	2	3	4	5
z1	3/w1	1/w1	1/w1	2/w2	5/w1
z2	4/w2	1/w1	2/w1	3/w1	1/w2
z3	5/w2	2/w2	4/w1	5/w2	3/w1

 

 

Декомпозиция автоматов

 

Провести декомпозицию заданного автомата на автоматы с двумя состояниями. Определить вид компонентных автоматов и функции структуры сети.

 

Вариант 1

 

	1	2	3	4	5	6	7
z1	3/w1	5/w2	5/w1	6/w1	2/w1	6/w1	2/w1
z2	7/w1	4/w1	1/w2	1/w1	4/w1	7/w1	4/w1
z3	6/w2	7/w1	1/w1	3/w1	7/w1	4/w1	5/w1

 

 

Вариант 2

 

	1	2	3	4	5	6	7
z1	2/w1	7/w1	5/w1	6/w1	3/w2	4/w1	2/w2
z2	1/w1	4/w2	1/w1	4/w2	2/w1	5/w1	7/w1

 

Вариант 3

 

	1	2	3	4	5	6	7
z1	2/w1	5/w1	6/w1	7/w1	7/w2	6/w1	5/w2
z2	4/w1	1/w2	1/w1	3/w2	3/w1	4/w1	3/w1
z3	6/w2	1/w1	2/w1	5/w1	4/w1	3/w1	4/w1

 

 

Вариант 4

 

	1	2	3	4	5	6	7
z1	6/w2	7/w1	1/w1	3/w1	7/w1	4/w1	5/w1
z2	7/w1	4/w1	1/w2	1/w1	4/w1	7/w1	4/w2
z3	3/w1	5/w2	5/w1	6/w1	2/w2	6/w1	2/w1

 

Вариант 5

 

	1	2	3	4	5	6	7
z1	2/w1	7/w1	5/w1	6/w1	3/w2	3/w1	2/w2
z2	1/w1	4/w2	1/w1	4/w2	2/w1	2/w1	7/w1

 

Вариант 6

	1	2	3	4	5	6	7
z1	7/w1	7/w2	6/w1	5/w2	6/w2	7/w1	1/w1
z2	3/w2	3/w1	4/w1	3/w1	7/w1	4/w1	1/w2
z3	5/w1	4/w1	3/w1	4/w1	3/w1	5/w2	5/w1

 

 

 

Вариант 7

 

	1	2	3	4	5	6	7
z1	3/w2	3/w1	2/w2	6/w1	7/w1	5/w1	6/w1
z2	2/w1	2/w1	7/w1	4/w2	4/w2	1/w1	4/w2

 

 

Вариант 8

 

	1	2	3	4	5	6	7
z1	1/w1	3/w1	7/w1	4/w1	5/w1	6/w2	7/w1
z2	1/w2	1/w1	4/w1	7/w1	4/w2	7/w1	4/w1
z3	5/w1	6/w1	2/w2	6/w1	2/w1	3/w1	5/w2

 

 

Вариант 9

 

	1	2	3	4	5	6	7
z1	5/w1	6/w1	7/w1	7/w2	3/w1	5/w2	5/w1
z2	1/w2	1/w1	3/w2	3/w1	7/w1	4/w1	1/w2
z3	1/w1	2/w1	5/w1	4/w1	6/w2	7/w1	1/w1

 

 

Вариант 10

	1	2	3	4	5	6	7
z1	3/w1	5/w2	5/w1	6/w1	2/w2	6/w1	2/w1
z2	2/w1	7/w1	5/w1	6/w1	3/w2	3/w1	2/w2

 

Структурные автоматы

Гонки в автомате

 

Кодирование состояний

Задача кодирования состояний является одной из первых задач канонического метода структурного синтеза автоматов. Напомним, что кодирование заключается в установлении взаимно однозначного соответствия между множеством А = {а₁,…,а_N} состояний автомата и множеством r-компонентных векторов {К₁,…, К_m), К_m= (е_m1,…,e_mr}, где е_mr - состояние r-го элемента памяти,  r = 1,…,m.

Переход автомата из одного состояния в другое осуществляется за счет изменения состояний элементов памяти. Так, если автомат переходит из состояния а_r с кодом 0101 в состояние а_S  с кодом 1001, то это означает, что триггер Т₁  переходит из состояния 0 в состояние 1, триггер Т₂ - из состояния 1 в состояние 0, а состояние триггеров Т₃, и Т₄ не изменяется.

 

Проектирование автомата

Проектирование автомата заключается в определении функций {y_i,v_j | i=1,…,m, j=1,…,k} и синтезе в заданном базисе схемы, реализующей эти функции.

Выходные функции определяются по матрице выходов автомата: после кодировки входов, выходов и состояний автомата матрица выходов представляет таблицу, описывающую m булевых выходных функций.

Функции возбуждения элементов памяти для случая триггера типа линии задержки также просто получаются из матрицы переходов автомата заменой входов и состояний автомата их кодами.

 Для счётного триггера эти функции получаются как результат операции сложения по модулю два кодов текущего и следующего
состояний.

Пример. Пусть автомат описывается матрицами переходов и выходов (табл.2.3 и 2.4).

Таблица 2.3					Таблица 2.4
	a1	a2	a3	a4				a1	a2	a3	a4
z1	a2	a2	a3	a3			z1	w1	w2	w2	w1
z2	a4	a2	a1	a4			z2	w2	w2	w2	w1
z3	a4	a3	a2	a1			z3	w1	w1	w1	w2

 

 

Таблица 2.5
	00	01	11	10
00	0	1	1	0
01	1	1	1	0
11	0	0	0	1

Введём следующие кодировки для состояний, входов и выходов автомата (через переменные ai, Zj и wr): a1=00, a2=01, a3=11, a4=10,

Z1=00, Z2=01, Z3=11, w1=0,w2=1.

Перепишем в этой кодировке матрицу выходов, получим описание выходных
(в данном примере всего одной) функций (табл.2.5).

Таблица 2.6
	00	01	11	10
00	01	01	11	11
01	10	01	00	10
11	10	11	01	00

Если обозначить кодирующие переменные входа как x1 и x2, состояний как t1 и t2, выхода как y, то функция выхода будет иметь вид:

y=`t1•x2Ú`t1•t2•`x1 Út1•x1•`x2.

Если в качестве элемента памяти задан триггер типа линии задержки, то, заменив в табл.2.2 состояния на их коды, получим описание пары функций v1 и v2 (первый и второй столбец в
табл. 2.6).

По этой таблице

 v1=`t1•`t2•x2Ú`t1•x1Út1•`x2Ú`t2•`x1•x2.

v2=`x1•`x2Ú`t1•t2•x2Út2•x1•x2.

Если задан счётный триггер, то функции будут иметь вид, показанный в табл.2.7.

В этом случае функции имеют вид:

Таблица  2.7
	00	01	11	10
00	01	00	00	01
01	10	00	11	00
11	10	10	10	10

v1=`t1•`t2x•2Úx1•x2Út1•t2•x2,

v2=`t2•`x1•`x2Út1•xt•`x1•x2.

 

Рассмотрим ещё один пример.

Построим автомат-счётчик чисел от 0 до 9 с выходом на семисегментный индикатор. Индикатор имеет вид, как на рис.2.3. Числам сопоставляются выделенные сегменты индикатора в соответствии с
табл. 2.8.

На рис. 2.4 в качестве примера показана индикация цифры 5.

Таблица 2.8
число сегмент	0	1	2	3	4	5	6	7	8	9
1	1	1	1	1	1	0	0	1	1	1
2	1	1	0	1	1	1	1	1	1	1
3	1	0	1	1	0	1	1	0	1	1
4	1	0	1	0	0	0	1	0	1	0
5	1	0	0	0	1	1	1	0	1	1
6	1	0	1	1	0	1	1	1	1	1
7	0	0	1	1	1	1	1	0	1	1

Автомат Мура имеет 10 состояний от 0 до 9, 7 выходов, которые выделяют сегменты в соответствии с табл. 2.8 (1 означает, что сегмент виден, 0 – не виден). На единственный вход автомата поступает двоичный сигнал 0 или 1, 0 оставляет автомат (а значит, и число на индикаторе) в прежнем виде, 1 переводит автомат в следующее состояние и на индикаторе высвечивается следующее число. Значит, таблица переходов имеет вид как в табл. 2.9.

Таблица 2.9
Z\a	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	0

Для кодировки необходимо взять 4 элемента памяти. Закодируем состояния автомата последовательно кодами

0	1	2	3	4	5	6	7	8	9
0000	0001	0010	0011	0100	0101	0110	0111	1000	1001

 

Тогда таблица переходов запишется, как в табл.2.10.

 

Таблица 2.10
t1,t2,t3,t4 x	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001
0	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001
1	0001	0010	0011	0100	0101	0110	0111	1000	1001	0000

 

Если в качестве триггера выбрана задержка, то данная таблица описывает 4 функции возбуждения элементов памяти v1-v4 от переменных t1-t4 и х. Переменная х кодирует z: z1=0, z2=1. Первая функция v1 имеет вид как табл.2.11. Здесь для удобства выход четвёртого триггера вынесен в имя строки.

Таблица 2.11
t1,t2,t3 t4,x	000	001	010	011	100	101	110	111
0 0	0	0	0	0	1	-	-	-
0 1	0	0	0	0	1	-	-	-
1 0	0	0	0	0	1	-	-	-
1 1	0	0	0	1	0	-	-	-

 

 

Отсюда v1=t1×`t4 v t1×`x v t2×t3×t4×x.

 

Таблица 2.12
t1,t2,t3 t4,x	000	001	010	011	100	101	110	111
0 0	0	0	1	1	0	-	-	-
0 1	0	0	1	1	0	-	-	-
1 0	0	0	1	1	0	-	-	-
1 1	0	1	1	0	0	-	-	-

 

 

` v2= t2×`t4 v×t2×`x v t2×`t3 v `t2×t3×t4×x

 

 

Таблица 2.13
t1,t2,t3 t4,x	000	001	010	011	100	101	110	111
0 0	0	1	0	1	0	-	-	-
0 1	0	1	0	1	0	-	-	-
1 0	0	1	0	1	0	-	-	-
1 1	1	0	1	0	0	-	-	-

 

 v3= t3×`t4 v ×t3×`x v `t1×`t3×t4×x

 

Таблица 2.14
t1,t2,t3 t4,x	000	001	010	011	100	101	110	111
0 0	0	0	0	0	0	-	-	-
0 1	1	1	1	1	1	-	-	-
1 0	1	1	1	1	1	-	-	-
1 1	0	0	0	0	0	-	-	-

 

 

v4=`t4× x v t4×`x

Проектируемый автомат является автоматом Мура. Записав соответствие между состояниями и выходами, получим формулы для выходных функций.

Задание. Выпишите функции для каждого сегмента индикатора.

 

Упражнение

 

Кодирование

 

Для заданного автомата построить кодирование состояний, свободное от гонок методом развязывания пар состояний.

 

 

Вариант 1

 

	1	2	3	4	5	6	7	8
z1	8	2	4	4	7	2	7	8
z2	1	3	3	6	1	6	1	3
z3	1	5	6	4	5	6	4	1

 

Вариант 2

 

	1	2	3	4	5	6	7	8
z1	1	4	6	4	1	6	8	8
z2	1	2	3	2	5	1	5	3
z3	5	7	3	2	5	3	7	2

 

Вариант 3

 

	1	2	3	4	5	6	7	8
z1	4	7	3	4	5	3	7	5
z2	1	2	6	8	1	6	2	8
z3	3	6	3	5	5	6	7	7

 

 

Вариант 4

 

	1	2	3	4	5	6	7	8
z1	3	5	3	4	5	4	7	7
z2	1	4	1	4	5	6	5	6
z3	8	2	6	7	2	6	7	8

Вариант 5

 

	1	2	3	4	5	6	7	8
z1	3	5	3	8	5	7	7	8
z2	1	2	3	4	4	2	1	3
z3	4	6	5	4	5	6	8	8

 

Вариант 6

 

	1	2	3	4	5	6	7	8
z1	7	2	3	3	2	6	7	6
z2	1	2	1	4	5	2	4	7
z3	4	7	3	4	8	3	7	8

 

Вариант 7

 

	1	2	3	4	5	6	7	8
z1	4	7	5	4	5	8	7	8
z2	1	3	3	5	5	1	8	8
z3	2	2	6	7	6	6	7	2

 

Вариант 8

 

	1	2	3	4	5	6	7	8
z1	2	2	4	4	6	6	8	8
z2	1	1	3	3	5	5	7	7
z3	3	4	3	4	5	6	5	6

 

Вариант 9

 

	1	2	3	4	5	6	7	8
z1	5	6	7	8	5	6	7	8
z2	1	2	3	4	1	2	3	4
z3	4	5	3	4	5	7	7	3

 

Вариант 10

 

	1	2	3	4	5	6	7	8
z1	2	2	4	4	4	6	7	2
z2	7	2	3	5	5	3	7	2
z3	4	8	6	4	5	6	5	8

 

 

Синтез автомата

 

Для заданного автомата определить функции возбуждения элементов памяти

 

Вариант 1

 

	1	2	3	4	5	6	7	8
z1	3	4	2	5	7	2	3	1
z2	1	3	1	6	1	5	1	3
z3	6	5	6	4	2	3	4	2

 

Вариант 2

 

	1	2	3	4	5	6	7	8
z1	5	8	1	2	4	3	3	7
z2	1	2	3	2	7	1	5	3
z3	5	7	4	2	5	3	1	2

 

Вариант 3

 

	1	2	3	4	5	6	7	8
z1	4	6	2	3	4	2	7	5
z2	1	2	6	1	1	6	2	8
z3	2	6	3	4	5	3	6	7

 

 

Вариант 4

 

	1	2	3	4	5	6	7	8
z1	3	5	2	6	5	4	7	7
z2	2	4	1	4	7	6	5	6
z3	8	2	6	7	2	1	3	5

 

 

Вариант 5

 

	1	2	3	4	5	6	7	8
z1	3	5	4	7	5	4	7	2
z2	1	2	3	7	4	2	1	3
z3	7	6	5	3	6	6	8	1

 

 

Вариант 6

 

	1	2	3	4	5	6	7	8
z1	8	2	3	5	2	8	7	6
z2	1	2	1	4	5	2	4	7
z3	4	7	2	4	8	3	5	8

 

Вариант 7

 

	1	2	3	4	5	6	7	8
z1	4	7	5	4	2	3	7	5
z2	1	3	3	5	5	1	8	1
z3	2	2	6	7	6	6	7	2

 

Вариант 8

 

	1	2	3	4	5	6	7	8
z1	2	3	4	1	6	7	8	2
z2	4	1	3	2	2	5	1	7
z3	3	4	5	2	2	7	5	6

 

 

Вариант 9

 

	1	2	3	4	5	6	7	8
z1	5	6	7	8	1	6	3	2
z2	1	5	2	3	1	2	8	4
z3	4	5	3	4	5	7	6	3

 

 

Вариант 10

 

	1	2	3	4	5	6	7	8
z1	1	2	4	3	4	6	1	2
z2	7	2	3	5	5	3	7	2
z3	4	8	6	4	7	2	5	8

 

 

Синтез схем

Определения

Пусть задано множество Y элементов, каждый из которых имеет единственный выходной полюс и характеризуется числом входных полюсов и реализуемой этим элементом функцией от значений на входных полюсах. Значения переменных на входных и выходных полюсах элементов принимаются из множества {0,1}. Будем считать, что каждый элемент из Y определяет тип элемента и что в наличии есть неограниченное множество элементов данного типа.

Схемой назовём композицию элементов из Y, полученную отожде-ствлением (связыванием) выходов некоторых элементов с входами других элементов, при которой выполняются следующие свойства:

1. С каждым входом связано не более одного выхода.

2. В схеме не образуются контуры.

3. С каждым выходом может быть связано более одного входа.

Назовём эти свойства свойством корректности связей схемы.

Все несвязанные входы элементов схемы назовём её входами, несвязанные выходы элементов и некоторые выделенные связанные выходы элементов схемы назовём выходами схемы.

Пример схемы приведён на рис. 3.1.

Здесь x, y и z – входы схемы, g и f – её выходы, элементы 1 и 2 реализуют функцию конъюнкции, элемент 3 – функцию инверсии.

Можно показать, что если выполняются условия корректности, то на выходах схемы реализуются функции, равные суперпозиции функций элементов схемы.

 Для схемы 1: f=(x×y)×Z, g=x×y .

Множество Y назовём базисом схемы.

Задачей синтеза схем назовём задачу построения в заданном базисе Y для заданных функций F ={ f 1, f 2,…, fm } схемы, реализующей эти функции.

Будем оценивать решение числом элементов в схеме.

Одно из важных требований к результирующей схеме состоит в том, что она должна иметь минимальное число элементов. Прежде чем рассматривать решение задачи синтеза, ответим на вопрос: каким требованиям должен отвечать базис, чтобы в нём можно было построить схему для любых заданных функций?

Классы функций

Пусть задано некоторое множество функций M. Множество функций, которое может быть реализовано схемами в базисе M, называют классом, порожденным M, а само множество M называется порождающим множеством этого класса.

Рассмотрим некоторые классы функций.

Класс всех функций обозначим классом C. Порождающее множество этого класса называют функционально полным. В этих терминах поставленный выше вопрос можно сформулировать как вопрос о свойствах функционально полного множества элементов.

Монотонные функции

 

Определение. Два набора значений двоичных переменных a=<a1,a2,…,an> и b=<b1,b2,…,bn> назовём сравнимыми и будем писать a³ b, если "i i=1,…,n aI ³ bi. Здесь ³ понимается в обычном виде: 1>0.

Если a³ b и b³ a, наборы считаются несравнимыми.

Пример. Наборы a=<010111> и b=<010101> сравнимы и a³b. Набор a и c=<100111> несравнимы.

Определение. Функция f называется монотонной, если для любых двух наборов значений входных переменных a и b из того, что a³b, следует, что f(a)³f(b).

Свойства монотонных функций.

1. Нулевой набор значений сравним с любым набором и явля-ется меньшим любого из них. Значит, если монотонная функ-ция равна единице на этом наборе, то она равна единице и на любом наборе, т.е. равна константе. Точно так же, если на единичном наборе значений монотонная функция равна нулю, то она не может быть единицей ни на каком наборе, так как единичный набор больше всякого другого набора.

2. Пусть функция на наборе a, отличном от единичного, равна 1, и пусть значение I-й компоненты в нём равно 0. Это значит, что на наборе, который отличается только тем, что i-я пере-менная в нём равна 1, функция тоже примет единичное зна-чение. Это означает, что конъюнкции в ДНФ, соответствую-щие этим наборам, можно склеить по переменной xi. Точно так же, для набора со значением переменной 0 (т.е. с возмож-ным значением в конъюнкции переменной с инверсией) найдётся набор со значением переменной 1, что приведёт к склеиванию по этой переменной. Значит, в минимальной ДНФ монотонной функции нет переменных в инверсной форме.

Из этих свойств можно вывести, что:

1) суперпозиция монотонных функций будет функцией монотонной, т.е. множество монотонных функций образует класс монотонных функций, обозначаемый как M;

2) базисом класса М будут обе константы и пара функций – конъюнкция и дизъюнкция, т.е. множество {x × y, x Ú y, 0,1}.

Задача. Докажите, что константы должны присутствовать в базисе.

 

Самодвойственные функции

Определение. Для функции f( x1, x2,…, xn) функция называется двойственной к ней.

Обозначим двойственную функцию как f*.

Пример. Для функции (х ×у) двойственной будет функция ( `х `у) = x v y.

Можно показать, что двойственной функцией к f* будет функция f,

значит для х Úу двойственной будет х ×у.

Двойственной к х будет функция, равная х, двойственной к 0 будет 1.

Определение. Функция называется самодвойственной, если она равна своей двойственной.

Переменная x служит примером самодвойственной функции, так же как и функция инверсии переменной.

Свойства самодвойственных функций.

Таблица 3.1
х	у	f1	f2	f3	f4
0	0	0	0	1	1
0	1	0	1	0	1
1	0	1	0	1	0
1	1	1	1	0	0

1. Самодвойственная функция полностью определяется своим видом на верхней половине таблицы истинности. Действительно, если, например, значение функции на наборе
< a1, a2, …, a n> равно 0, то значение функции на инверсном наборе < ` a1, ` a2, …, ` a n> должно быть равно 1.

2. Из первого свойства вытекает, что число различных функций от n переменных равно 2 ^m, где m=2 ^n-1.

3. Построим все функции от двух переменных. Их будет 4 в соответствии с возможными значениями на верхней половине таблицы: 00,01,10,11. Эти функции приведены в табл. 3.1. Как видно из таблицы, первые две функции совпадают с переменными, две последние – с инверсиями переменных. Отсюда следует свойство: самодвойственных функций, существенно зависящих ровно от двух переменных, нет.

4. СДНФ самодвойственной функции будет иметь ровно 2^n-1 конъюнкций

5. Суперпозиция самодвойственных функций будет функциейсамодвойственной. Множество самодвойственных функций образуют класс, который принято обозначать как D. Базисом класса является функция трёх переменных { x × ` y Ú x × ` z Ú ` y × ` z}.

 

Линейные функции

Рассмотрим класс функций, порождённых множеством
F={ x × y, x Å y, 1}.

Из того, что xÅ1=`х, следует, что в данном базисе реализуется инверсия, которая вместе с конъюнкцией даёт возможность построить любую функцию. Значит, данный базис порождает класс всех функций – класс С.

Сравним таблицы функции сложения по модулю два и дизъюнкции (табл.3.2)

Таблица 3.2

а	в	аÚв	аÅв
0	0	0	0
0	1	1	1
1	0	1	1
1	1	1	0

Из таблицы видно, что а Ú b = (а Å b) Úа × b.

       Если а и в такие, что имеет место равенство а ×в = 0, то такие переменные называются ортогональными. Для ортогональных переменных
а Úв = (а Åв).

Если рассматривать СДНФ любой функции, то можно показать, что в ней любая пара конъюнкций ортогональна. Это приводит к следующему алгоритму построения записи функции в рассматриваемом базисе:

· записать функцию в СДНФ;

· заменить в СДНФ символы дизъюнкции на символы сложения по модулю два;

· заменить все инверсии по формуле `х = (х Å1);

· раскрыть скобки, пользуясь свойством дистрибуции
х ×( y Å z) = x × y Å x × z;

· сделать сокращения, используя свойство х Åх = 0, х Å0= х.

В результате получается запись функции в форме, которую представим в общем виде как

f=C0 Å C1 × x1 Å C2 × x2 Å … Å Cn × xn Å C(n+1) × x1 × x2 Å … Å Cm × x1 × x2 ×… × xn, где С0, С1, С2,…Cm принимают значения 0 или 1.

Это представление называется полиномом Жегалкина, а алгебра с сигнатурой { x × y, x Å y, 1} – алгеброй Жегалкина.

Пример. Построим полином Жегалкина для функции импликации. По её таблице запишем СДНФ этой функции:

а ®в = `а `в Ú `ав Ú ав, после замены дизъюнкций на сложение по модулю два имеем:  а ®в = `а `в Å `ав Å ав = (а Å1)(в Å1) Å(а Å1) ×в Åа ×в = =а ×в Åа Åв Å1 Åа ×в Åв Åа ×в = а ×в Åа Å1.

Определение. Функция называется линейной, если её полином Жегалкина не содержит конъюнкций.

Общий вид линейной функции f = C0 Å C1 × x1 Å C2 × x2 Å… Å Cn × xn.

Таким образом, число различных линейных функций от не более чем n переменных определяется формулой N = 2 ⁿ⁺¹.

Суперпозиция линейных функций есть функция линейная, следовательно, множество линейных функций образует класс линейных функций, обозначаемый как L.

Базисом класса L служит множество { x Å y, 1}.

 

Функциональная полнота

 

Мы выделили 5 классов функций алгебры логики. Различных классов функций гораздо больше: так, a-функции образуют свой класс, пересечение классов снова будет классом.

Американский математик Э.Пост установил, что классы М, D, L, C1 и C0 являются предполными, и других предполных классов в С нет.

Решение задачи формулируется как теорема  Э.Поста.

Теорема. Для того чтобы множество функций F порождало класс всех функций С, необходимо и достаточно, чтобы это множество содержало, по крайней мере, одну немонотонную, одну несамодвойственную, одну нелинейную, одну несохраняющую константу ноль и одну несохраняющую константу единица функцию.

Необходимые условия формулируются из результатов Поста о предполных классах. Необходимо, чтобы в F по отношению к любому из этих классов была функция, не принадлежащая классу. Действительно, если в рассматриваемом множестве нет, например, несамодвойственной функции, то в результате суперпозиций будут реализовываться только самодвойственные функции, то есть нельзя получить, например, конъюнкцию, которая не является самодвойственной.

Достаточность доказывается конструктивно. Покажем, как из функций, удовлетворяющих условиям теоремы Поста, получить инверсию и конъюнкцию или дизъюнкцию, составляющие функционально полный базис.

Пусть множество содержит функцию f₀, не сохраняющую константу ноль, f₁, не сохраняющую константу единица, f₂ – немонотонную, f₃ – несамодвойственную и f₄ – нелинейную функцию (все функции не обязательно различные).

f₀(0,0,…,0) = 1. Для этой функции возможны два варианта значений

f₀(1, 1,…,1). 

Если f₀ (1, 1,…,1) = 1, то функция является b-функцией, и при подстановке вместо всех аргументов произвольного одного аргумента она превращается в константу 1. Имея константу 1, из функции f₁ получаем константу 0, так как f₁(1, 1,…,1) = 0.  

Если f₀ (1, 1,…,1) = 0, то функция является d-функцией и при подстановке вместо всех аргументов произвольного одного аргумента она превращается в инверсию. В этом случае рассмотрим функцию f₃. Для неё найдется набор значений аргументов <a₁, a₂,…, a _n>, такой, что

 f(a₁, a₂,…, a_n) = f(`a<sub>1</sub>, `a₂,…, `a_n).

В функцию f₃ поставим произвольную переменную в прямой форме, если компонента набора a_i равна 1, и в инверсной форме, если равна 0, то получим константу, равную f(a₁, a₂,…, a_n). Из неё с помощью инверсии получается вторая константа.

С помощью констант из функции f₂ можно получить инверсию.

Для неё найдется два соседних набора, таких, что на меньшем наборе функция равна единице, а на большем – нулю. Если подставим в f₂ константы этого набора, где они совпадают, и произвольную перемен-ную, где наборы отличаются, получим инверсию этой переменной.

 Константы и инверсия позволяют получить конъюнкцию перемен-ных из функции f₄. Запишем эту функцию в виде полинома Жегалкина, выделим в нём первое вхождение переменных в конъюнкцию, и все пе-ременные, кроме переменных конъюнкции, заменим константой 0, а переменные в конъюнкции заменим произвольно на два различных аргумента, например на x и y. В результате возможны, с точностью до инверсии (константы С₀ в полиноме), следующие варианты:

1) xy; 

2) xyÅx;

3) xyÅy;

4) xyÅxÅy.

Таблица 3.3
f	M	D	L	C1	C0
0	+	х	+	х	+
1	+	х	+	+	х
‘x	х	+	+	х	х
xÚy	+	х	х	+	+
x×y	+	х	х	+	+
x®y	х	х	х	+	х
xÅy	х	х	+	х	+
x»y	х	х	+	+	х
‘(x×y)	х	х	х	х	х
`(xÚy)	х	х	х	х	х

В первом случае получаем конъюнкцию, что и необходимо получить, во втором варианте полученная функция равна функции `xy, из которой с помощью инверсии получим конъюнкцию. То же самое можно сказать и о третьем варианте, где функция равна `yx. Для последнего варианта функция равна дизъюнкции.

Теорема доказана.

В табл. 3.3 показана при-надлежность простейших функций к предполным классам. Здесь + озна-чает, что функция принадлежит, а
 х – означает, что функция не принадлежит к классу, символом ‘ обозначена инверсия.

Из таблицы видно, что функциональной полнотой обладают множества {` x , x Ú y }, {` x , x × y }, { x × y , x Å y , 1}. { x ® y, 1}. Особый интерес представляют 2 последние функции, составляющие монофункциональ-ный базис. Такие функции, отве-чающие всем условиям теоремы Поста, получили название функций шефферовского типа.

Теорема позволяет определить, является ли заданное множество функционально полным, если нет, то какой функции в нём не хватает. Можно решать задачу построения функции шефферовского типа от более чем двух переменных. Это должна быть d-функция, так как она не сохраняет константы. Как  d-функция она немонотонна, и дальше нужно распределить единицы и нули в таблице так, чтобы функция была нелинейной и несамодвойственной.

 

Плоские схемы

Полнота для класса плоских схем определяется результатами Тоника, который свел условия полноты к условиям реализации в рассматриваемом базисе плоской схемы для функции сложения по модулю два (или ее инверсии), через которые реализуется схема пересечения двух сигналов (известная как “схема Тоника”), приведенная на рис.3.2.

Можно показать, что в одноэлементном базисе функция сложения по модулю два реализуется плоской схемой из 4 элементов (рис.3.3), следовательно, функция шефферовского типа представляет собой полный базис для плоских схем.

Аналогичную схему можно построить и в классическом базисе {x&y, xÚy, `x}. Она имеет 5 элементов.

Можно предложить метод синтеза плоских схем, состоящий из следующих шагов:

· построим схему для заданных функций;

· расположим её на плоскости таким образом, чтобы в схеме число пересечений было минимальным;

· заменим каждое пересечение схемой Тоника, после чего каждый из элементов схемы Тоника заменим схемой в заданном базисе.

Легко видеть, что число элементов в схеме при этом увеличится на произведение числа пересечений на число элементов в реализации каждого пересечения.

Один из методов сокращения числа элементов в плоской схеме заключается в том, что предложено учитывать значения функций, которые участвуют в пересечении. Так, если эти функции таковы, что у них одновременно обе функции не могут принимать значение 1, то число элементов в реализации их пересечения можно сократить вдвое.

Второй способ состоит в том, что предлагается сразу искать схему, которая допускает хорошую (а лучше плоскую) укладку.

Далее определяются условия функциональной полноты, если допустимы лишь такие суперпозиции, которым сопоставлены схемы с ограниченной глубиной связи между ее элементами. Особое внимание уделено схемам с глубиной связи, равной единице. В приведенной трактовке этому соответствуют схемы с нулевым разбросом сигналов на входах всех элементов.

Методы синтеза схем

Рассмотрим два подхода к синтезу схем – декомпозицию и факторизацию.

Метод факторизации

Метод факторизации заключается в алгебраических преобразованиях описаний, заданных для реализации функций, с тем, чтобы выразить их через функции базиса. При этом важной частью преобразований является учёт числа входов элементов базиса, что обеспечивается вынесением за скобки и использованием свойств дистрибутивности функций.

Рассмотрим применение метода для классического базиса, состоящего из элементов {2-И, 2-ИЛИ, НЕ}, и для монофункциональных базисов {И-НЕ} или {ИЛИ-НЕ.}

Метод декомпозиции

Метод декомпозиции ещё называют методом от выходов к входам. Он состоит из последовательности шагов:

1. Определяется множество функций, называемых множеством непостроенных функций (обозначим как Fн). Вначале Fн=F.

2. Выбирается функция fÎFн и она удаляется из Fн. Выбирается элемент gÎY. Предполагается, что f реализуется на выходе
элемента g.

3. Определяются функции (называемые образующим списком), которые необходимо подать на вход элемента g, чтобы на выходе его получить f.

4. Эти функции, за исключением входных переменных, вносятся в множество Fн.

Шаги 2 -4 повторяются до тех пор, пока множество Fн не станет пустым. Для того чтобы получить решение, любая из функций образующего списка для f должна быть проще функции f. Самыми простыми считаются входные переменные, для других функций каждый метод предлагает своё понятие простоты.

Рассмотрим работу метода на примере реализации функции сложения по модулю два от двух переменных в одноэлементном базисе, состоящем из элемента 2-И-НЕ.

Запишем таблицу для элемента базиса (табл. 3.4) и перепишем её в виде табл.3.5, где символом x обозначено значение «что угодно». Например, 2-я строка таблицы означает, что если на первом входе элемента – нулевое значение, то независимо от значения на втором входе значение на выходе элемента равно единице.

Запишем функцию в векторном виде как f = (aÅb) = <0110>.

При построении образующего списка будем исходить из того, что для реализации на выходе элемента 0 необходимо на оба входа
подать 1, для реализации 1 необходимо на один вход подать 0, на другой – что угодно. Образующий список для f в этом случае будет иметь вид {<1x01>,<10x1>}.

Таблица 3.4
a	b	j
0	0	1
0	1	1
1	0	1
1	1	0
Таблица 3.5
a	b	j
0	x	1
x	0	1
1	1	0

Будем оценивать сложность функции числом неопределённых значений в ней. Будем при этом исходить из того, что чем больше неопределённость функции, тем легче доопределить её до переменной. Из этой оценки следует, что вариант образующего списка {<1001>,<1хx1>} нас не устраивает, так как в этом варианте первая функция списка имеет ту же сложность, что и исходная.

Представим всё решение в виде рис. 3.6. На выходе 2-го элемента верхняя функция дополняется до переменной b=<0011>, нижняя функция элемента 3 – до функции а=<0101>. На входе 5-го элемента нижняя функция дополняется до b, верхняя функция 4-го элемента – до а.

Результирующая схема приведена на рис.3.7.

К методу декомпозиции можно отнести и метод каскадов Поварова, основанного на разложении К. Шеннона. Функция представляется как f(x1,x2,…,xn) = x×f(x=1) Ú`x×f(x=0), конструкция из элемента дизъюнкции и 2-х элементов конъюнкции образует каскад, на входе которого функции не зависят от переменной х и в этом смысле более просты, чем исходная функция.

В этом методе результат неоднозначен и зависит от порядка выбора переменных, по которым проводится разложение. Если функцию можно представить как сложение по модулю два переменной и некоторой функции f” от остальных переменных, то f” = f(x = 1) =`f(x = 0).

Пример. Построим схему для функции от 4 переменных, представленную в виде вектора

f(a, b, c, d) = <0110100101000101>

Начнём разложение с разложения по a. Получим
f1 = f(a = 0) = <01101001>, f2 = f(a = 1) = <01000101>.

Разложим f1 по переменной b, получим

f11 = f1(b = 0) = <0110>, f12 = f1(b = 1) = <1001>.

Замечаем, что f11 =`f12 = `c×dÚ c×`d.

Эта функция не минимизируется, реализуем её в базисе

{2-И, 2-ИЛИ, НЕ}.

Разложим f2 по переменной b, получим:

f21=f2(b=0)=<0100>, f22=f2(b=1)=<0101

Замечаем, что f22=переменной d, f21 =(`c×d).

Окончательно решение примет вид как на рис. 3.8.

 

 

Упражнения

 

Функциональная полнота

Определить, образует ли заданная функция функционально полный базис. Если нет, то какие функции необходимо добавить, чтобы они вместе с заданной функцией образовали базис?

а) f = (a®`bc) Å`ca ;

б) f = (ab®cd)v(aÅb)`d ;

в) f = a b`c v`a b`c v`a`bc va`b`c ;

г) f = a b`c v`a b c v a`bc vabc ;

д) f = (aÅb)cv (avbv`c) ® abc;

е) f = (cÅb)v ac(`b®d)vd&(⌐(c®a));

ж) f = ((a®b) Åac)&(cÅb). `

Синтез схем

1. Построить схему для заданной пары функций методом факторизации в классическом базисе {2И, 2ИЛИ, НЕ} (в скобках – число элементов в схеме).

а) {f1 =`a`b`c v `a b c v ac, f2= `a`b`c v a` b c } (не более 7 эл-тов);

б) {f1 =`a`c v `b`с v d (b v c),
 f2 = a b`d v a`d v c`d v a`b d } (не более 8 эл-тов);

в) {f1= a`b v`a b с v a`b c),
 f2 = `a v a`b v c`d v a`b d } (не более 4 эл-тов);

г) {f1= a`b v`a b с v a`b c,
 f2 = a ®(a`b) v a`b c } (не более 4 эл-тов);

д) {f1= a`b v`b c v a`b c,
 f2 = a `b v `a b c v a b`c } (не более 5 эл-тов);

е) {f1 = a`b v`a b c v `a b`c, f2= a b c } (не более 5 эл-тов);

ж) {f1 = Ø(a`b v`a b c v `a b`c),
f2 = a v `a b v `b c } (не более 5 эл-тов).

 

2. Построить схему для заданной функции методом декомпозиции в классическом базисе {2И, 2ИЛИ, НЕ}, используя разложение К. Шеннона

а) {f = (01101001000111101010010100011110)};

б) {f = (00111101110000100101000110101110)};

в) {f = (00101101000111101010010100011110)};

г) {f = (10011101011000100101000110101110)};

д) {f = (00011101111000100101000110101110)};

е) {f = (11011101001000100101000110101110)};

ж) {f = (11010010001011010101101010100101)};

з) {f = 10100101000111101010010100011110) }).

 

3. Построить схему для заданной функции методом декомпозиции в монофункциональном базисе {3И-НЕ}

a) {f: T1 = (001, 010, 100)};

b) {f: T1 = (001, 010, 100, 111)};

c) {f: T1 = (000, 011, 100, 110)};

d) {f: T1 = (000, 011, 100)};

e) {f: T1 = (010, 100, 101)};

f) {f: T1 = (000, 110, 101)};

g) {f: T1 = (000, 011, 101)}.  

 

4. Построить методом факторизации в классическом базисе {2И, 2ИЛИ, НЕ} плоскую схему с внешним доступом для заданной пары функций

а) {f1 = a b c v `a` b c, f2= `a b`c v `a b c } (не более 6 эл-тов);

б) {f1 =`a v`b a, f2= (`a ®b)`c v c } (не более 6 эл-тов);

в) {f1 = (b ® a)`d v d, f2= (a ®b)`c v c} (не более 6 эл-тов);

г) {f1= a b`c v a`b`c v a b c, f2= a`b`c v a`c v b`c} (не более 7 эл-тов);

д) {f1 = b`c v a`b v a c, f2= b`c v a`b } (не более 5 эл-тов);

е) {f1 = `a`b v a c, f2= Ø (b a v `b) } (не более 7 эл-тов).

 

Эксперименты над автоматами

Дерево преемников

Введем предварительно ряд понятий. Под a-множеством автомата S будем понимать любое конечное множество его состояний, причем элементы этого множества не обязательно различны. Множество, состоящее из единственного элемента, называется простым; содержащее два или более одинаковых элементов - кратным. Множество назовём однородным, если оно состоит из одинаковых элементов. Например, множество {a3} простое, {a2, a3, a2} – кратное, {a3, a3, a3} – однородное.

A-группа есть множество a-множеств автомата S, в котором число элементов во всех входящих в A-группу a-множеств равно m и совпадает с числом элементов в А(S). A-группа называется простой, если все
a-множества в ней простые, однородной, если все a-множества в нём однородные.

Предположим, что G есть A-группа, содержащая a-множества
σ1, …, σr.  Тогда z_i¹ z_i²...z_i^k -преемником G будет другая A-группа, построенная согласно следующим правилам:

1. Разбиваем каждое множество σ_i на такие подмножества, что два состояния σ_i включаются в одно и то же подмножество тогда и только тогда, когда они вырабатывают одинаковые реакции на входную последовательность z_i¹ z_i²...z_i^k. Считаем каждое подмножество как
σ-множество, а множество всех таких множеств как A-группу, обозначенную через G ^*.

2. В a-множествах из G ^* заменяем каждое состояние его преемником относительно входной последовательности z_i¹ z_i²...z_i^k. Полученная
A-группа есть z_i¹ z_i²...z_i^k- преемник G.

Дерево преемников есть структура, определенная для данного автомата S и заданного множества допустимых начальных состояний A ( S ). Структура состоит из ветвей, расположенных в последовательных уровнях, причем высшим уровнем является "нулевой", следующий за высшим является "первый" уровень и т. д. Нулевой уровень дерева содержит единственную ветвь, называемую начальной ветвью.

В дереве преемников, построенном для автомата с входным алфавитом { Z ₁ ,..., Z _p }, каждая ветвь в k-м уровне (k ³ 0) расщепляется на p ветвей, представляющих Z ₁ ,..., Z _p соответственно и являющихся ветвями в (k +1)-м уровне. Ветвь, представляющая входной символ z_i , называется "ветвью z _i".

Путем по дереву называется последовательность из l таких ветвей, что каждая следующая порождается предыдущей. Если k-я ветвь этого пути есть z _i ^k, то говорят, что этот путь описывает входную последовательность z_i ¹ ,..., z _i ^k. Таким образом, первые (k + 1) уровней дерева преемников содержат p ^k путей, описывающих все возможные входные последовательности длиной k, которые могут быть построены из p входных символов.

Каждая ветвь в дереве преемников, построенном для S и A ( S ), связана с A-группой, с начальной ветвью связана A ( S ). Если ветвь b связана с A-группой G, то ветвь z_i, которую порождает b, связана с z_i - преемником G. A-группы, связанные с ветвями k-го уровня (k ³ 1), могут быть определены из A-групп, связанных с ветвями (k-1)-го уровня.

Данное дерево преемников по своему протяжению бесконечно. Вводят понятие "усеченного" варианта путем формулировки ряда "правил завершения". Оконечной ветвью называют ветвь, которая не порождает каких-либо ветвей следующего уровня. Правило завершения определяет, когда ветвь становится оконечной.

 

Диагностический эксперимент

Диагностическим деревом называют дерево преемников, в котором ветвь b k-го уровня становится оконечной, если удовлетворяется одно из следующих условий:

· A-группа, связанная с b, содержит кратное a-множество.

· A-группа, связанная с b, связана с некоторой ветвью уровня, предшествующего k-му.

· Имеется ветвь k-го уровня (возможно, сама ветвь b), связанная с простой A-группой.

Диагностическим путем называется любой путь в диагностическом дереве, оконечная ветвь которого связана с простой А-группой.

Диагностической последовательностью для S и A ( S )={a₁,a₂,...,a _n} называется любая входная последовательность, которая, будучи приложенной к S|a₁, S|a₂,...S|a _n, дает в результате n различных выходных последовательностей (здесь как S|a₁ обозначен автомат S в состоянии a1).

Входная последовательность, описанная диагностическим путем в диагностическом дереве, построенном для S и А(S), есть диагностическая последовательность для S и А (S).

Рассмотрим построение диагностического дерева на примере автомата S1. У него множество состояний S = {1,2,3,4,5,6,7,8,9}, множество входных сигналов X = {α, β}, множество выходных сигналов Y = {0,1}.

Таблицы переходов и выхода S 1 представлены в табл.4.1. Множество допустимых состояний А(S) = {4,5,6,7,9}.

 

 

Таблица 4.1
	YS	1	2	3	4	5	6	7	8	9
Y	α	0	0	0	1	1	1	0	1	0
	β	1	1	1	1	1	0	1	1	0
S	α	1	1	5	3	2	7	8	5	2
	β	4	5	1	4	6	3	4	9	8

Шаг 1

На нулевом уровне дерева находится множество допустимых состояний A(S).

Найдем α-преемник А-группы A(S). Для этого разбиваем каждое
a -множество из A(S) на подмножества, которые вырабатывают одинаковые реакции на входную последовательность α. Состояния {4,5,6} вырабатывают выходной сигнал 1, а состояния {7,9} дают выходной
сигнал 0. Таким образом, получаем А-группу G'={4,5,6}{7,9}.

Затем в a-множествах из G' заменяем каждое состояние его преемником относительно входной последовательности α. Получаем следующую A-группу {3,2,7}{8,2}. Данная А-группа является
α-преемником A(S) и связана с ветвью α первого уровня.

Полученная А-группа не удовлетворяет условиям окончания ветви диагностического дерева.

 

0	{4,5,6,7,9}
	α	β
1	{3,2,7}{8,2}

Шаг 2

Найдем β-преемник А-группы A(S). Для этого разбиваем каждое
a -множество из A(S) на подмножества, которые вырабатывают одинаковые реакции на входную последовательность β. Состояния 4,5,7 вырабатывают выходной сигнал 1, а состояния 6,9 вырабатывают выходной сигнал 0. Таким образом получаем А-группу G' = {4,5,7}{6,9}.

Затем в a -множествах из G' заменяем каждое состояние его преемником относительно входной последовательности β. Получаем следующую A-группу {4,6,4}{3,8}. Данная А-группа является
β-преемником A(S) и соединена с ветвью β первого уровня.

Полученная А-группа является кратной, поэтому ветвь, связанная с данной А-группой, является оконечной ветвью дерева.

0	{4,5,6,7,9}
	α	β
1	{3,2,7}{8,2}	{4,6,4}{3,8}

Шаг 3

Рассмотрим построение второго уровня дерева. Для этого находим α и β-преемников А-группы {3,2,7}{8,2}, расположенной на втором уровне дерева.

α-преемником является А-группа {1,8}{5}{5}{1}, β-преемником является {1,5,4}{9,5}.

0	{4,5,6,7,9}
	α		β
1	{3,2,7}{8,2}		{4,6,4}{3,8}
	α	β
2	{5,1,8}{5}{1}	{1,5,4}{9,5}

Шаг 4

Построение третьего уровня дерева производим аналогично: для А-групп третьего уровня находим α- и β-преемников.

А-группа {4,6,4}{8}{6} содержит кратное σ-множество {4,6,4}, поэто-му ветвь дерева, связанная с данной А-группой, является конечной.

 

0	{4,5,6,7,9}
	α				β
1	{3,2,7}{8,2}				{4,6,4}{3,8}
	α		β
2	{5,1,8}{5}{1}		{1,5,4}{9,5}
	α	β	α	β
3	{2,5}{1}{5}{1}	{6,4,9}{6}{4}	{1}{2,3}{2}{2}	{4,6,4}{8}{6}

Шаг 5

Построение четвертого уровня дерева производим аналогично.

Одна из полученных А-групп {1}{2}{1}{2}{1} состоит из простых
σ-множеств. Поэтому все ветви этого уровня являются оконечными. На этом построение диагностического дерева заканчивается.

 

0	{4,5,6,7,9}
	α									β
1	{3,2,7}{8,2}									{4,6,4}{3,8}
	α					β
2	{5,1,8}{5}{1}					{1,5,4}{9,5}
	α			β		α			β
3	{2,5}{1}{5}{1}			{6,4,9}{6}{4}		{1}{2,3}{2}{2}			{4,6,4}{8}{6}
	α	β	α		β		α	β
4	{1}{2} {1}{2} {1}	{5,6} {4}{6} {4}	{7,3} {2}{7} {3}		{3,8} {4}{3} {4}		{1}{1,5} {1}{1}	{4}{5,1} {5}{5}

 

Диагностическим путем данного дерева является путь α, α, α, α. Поэтому диагностической последовательностью для данного автомата S и данного множества начальных состояний A(S)={4,5,6,7,9} является последовательность (α, α, α, α).

В таблице приведены реакции состояний 4,5,6,7,9 на входную последовательность α,α,α,α

Начальное состояние	Реакция на α,α,α,α
4	1010
5	1000
6	1011
7	0110
9	0000

Для множества начальных состояний {4,5,6,7,9} диагностическая задача имеет решение с помощью простого безусловного эксперимента, но возможны случаи, когда диагностическая последовательность не существует.

Рассмотрим пример для автомата S1 и множества допустимых состояний {1,2,3,4,5}. По алгоритму, описанному ранее, построим диагностическое дерево.

0	{1,2,3,4,5}
	α	β
1	{1,1,5}{3,2}	{4,5,1,4,6}

Все А-группы первого уровня являются кратными, т.е. для данного S и А(S) не существует диагностической последовательности, и это означает, что не существует решения диагностической задачи для данных S и А(S) с помощью простого безусловного эксперимента.

 

Установочный эксперимент

Установочным деревом называют дерево преемников, в котором ветвь b k-го уровня становится оконечной, если удовлетворяется одно из следующих условий:

· A-группа, связанная с b, связана с некоторой ветвью уровня, предшествующего k-му.

· Имеется ветвь k-го уровня (возможно, сама ветвь b), связанная с однородной A-группой.

Установочным путем называется любой путь в установочном дереве, оконечная ветвь которого связана с однородной А-группой.

Для автомата табл. 4.1 приведём установочное дерево, построенное при условии, что A(S)={3, 4, 5, 7}. 

{3, 4, 5, 7}
1	α		β
	{5, 8},{3, 2}		{1,4, 6, 4}
2	α	β	α	β
	{2, 5}, {1, 5}	{6, 9},{1, 5}	{1}, {3, 7, 3}	{4, 4, 4},{3,3}

 

Получаем в итоге, что установочный эксперимент состоит в подаче на вход автомата последовательности (β β). Если при этом выходное слово равно (11), то автомат установлен в состояние 4, если выходное слово равно (10), то автомат находится в состоянии 3.

 

 

Упражнения

 

Установочные эксперименты

Для автоматов, приведённых в предыдущем разделе, построить установочные деревья для следующих множеств допустимых начальных состояний.

Вариант 1 A(S)={2,3,4}.

Вариант 2 A(S)={1,3,4}.

Вариант 3 A(S)={1,3,5}

 

 

Формальные грамматики

Порождающая грамматика

Одна из задач, которая решается в формальных языках, заключается в выявлении множества слов, которые могут быть построены с помощью данной грамматики. Чаще решается обратная задача: для заданного языка построить грамматику, которая порождает этот язык. Такие грамматики называются порождающими. Пример решения такой задачи рассмотрены выше (пример 5). При этом необходимо определить алфавиты V, N, описать множество правил P. Если алфавит V определяется однозначно из вида слов языка, то алфавит N можно определить по-разному. В примере 5 можно не определять понятие <знак>, тогда правила p1, р2 и p3 заменятся двумя правилами

 p1: <число> ::= + <модуль>,
 p2: <число> ::= - <модуль>.

Одна из задач, которая решается в формальных языках, заключается в выявлении множества слов, которые могут быть построены с помощью данной грамматики. Чаще решается обратная задача: для заданного языка построить грамматику, которая порождает этот язык. Такие грамматики называются порождающими.

Порождающая грамматика G = (V, N, S, P) позволяет выводить (порождать) цепочки языка из некоторой начальной цепочки с помощью заданных правил замены (подстановки). Вывод — это пошаговый процесс, в котором из цепочки, полученной на предыдущем шаге, путем применения правил замены можно получить новую цепочку.

Правило вывода записывают в виде: a ® b.

Цепочку a называют левой частью правила вывода, а цепочку b — правой.

Цепочка a должна содержать вхождение хотя бы одного символа нетерминального алфавита N.

Буквы терминального алфавита называют терминальными символами (терминалами), а нетерминального алфавита — нетерминальными символами (нетерминалами). Любую цепочку в терминальном (нетерминальном) алфавите называют терминальной (нетерминальной) цепочкой.

Пример. Четверка G = ({a,b}, {S, A, B}, S, {S ® aAB, aA ® aB, S ® bb, B ® aB}) задает грамматику с терминальным алфавитом V = {a,b}, нетерминальным алфавитом N = {S, A, B}, аксиомой S и множеством правил вывода P = {S ® aAB, aA ® aB, S ® bBb, B ® aB, B ® bb}.

Цепочка d непосредственно выводима в грамматике G из цепочки g, если существуют такие цепочки s и r и такое правило вывода a ® b из P, что g = sar (т. е. существует вхождение левой части правила вывода в цепочку g), а d = sbr.

Говоря другими словами, непосредственная выводимость подразумевает получение цепочки d из цепочки g за одно применение какого-либо правила вывода.

В вышеприведенном примере цепочка aAB непосредственно выводима из цепочки S, а цепочка aB — из цепочки aA.

Цепочка d выводима в грамматике G из цепочки g (обозначим как g ├ d), если найдутся такие слова a0 = g, a1, a2, …, an = d, что a0├ a1 ├…├ an.

Выводом в грамматике G называют саму последовательность слов a0 = g, a1, a2, …, an = d, таких, что a0 ├ a1 ├ a2 ├ … ├ an..
В вышеприведенном примере цепочка aAaB выводима из цепочки S.

Выводом же будет цепочка слов S ├ aAB ├ aAaB.

Понятия непосредственной выводимости, выводимости и вывода могут быть сопоставлены известным из теории графов понятиям непосредственной достижимости, достижимости и пути (для ориентированных графов) соответственно.

Язык, порождаемый грамматикой G, — это множество L(G) всех терминальных цепочек, выводимых из аксиомы грамматики:

L(G) = {x: S ├ x, x Î V+}.

Таким образом, целью вывода является получение из аксиомы цепочки, не содержащей нетерминальных символов, путем последовательного применения правил вывода. При этом следует отметить, что нет никаких ограничений на порядок применения правил вывода. Мы можем использовать любое правило в любом порядке произвольное количество раз.

Для сокращения записи правил с одинаковой левой частью примем следующее соглашение: вместо записи A ® a1, A ® a2, …, A ® an  будем писать A ® a1 ê, a2 ê … ê an.

Пример. Рассмотрим грамматику, моделирующую простейший фрагмент русского языка. Терминальными символами данной грамматики являются некоторые слова русского языка, а нетерминальными — грамматические категории: «предложение», «подлежащее», «сказуемое».

G1 = (V={землекоп, корабль, оркестр, играет, копает, плывет}, N={<предложение>, <подлежащее>, <сказуемое>}, S=<предложение>, P1).

Множество правил вывода P1 имеет вид:

{<предложение> ® <подлежащее> <сказуемое>,

<подлежащее> ® землекоп ê корабль ê оркестр,

<сказуемое> ® играет ê копает ê плывет}.

Первое правило вывода можно толковать следующим образом: «предложение — это подлежащее, за которым следует сказуемое».

Второе правило вывода означает: «подлежащее — это или “землекоп” или “корабль” или “оркестр”».

Третье правило вывода означает: «сказуемое — это или “играет” или “копает” или “плывет”».

Построим какой-нибудь вывод в грамматике G1:

<предложение> ├ <подлежащее> <сказуемое> ├ корабль < сказуемое > ├ корабль играет.

Отметим, что «смысл» (семантика) выводимой цепочки нас не интересует. Так что корабль может играть, оркестр плыть и т. д.

Таким образом, грамматику можно рассматривать как систему определений некоторых «понятий». Выделяется самое общее понятие — аксиома. В данном примере это <предложение>. Оно сводится к менее общим понятиям — нетерминалам. В конечном итоге получаем «конкретные объекты» – терминальные цепочки.

Пример. Рассмотрим грамматику G = (V, N, S, P), у которой

V = {a, b, c, Ú, Ù, Ø, (, )},

N = {I},

S = {I},

P = {I ® (I Ú I)

I ® (I Ù I)

I ® ØI

I ® a

I ® b

I ® c}.

Эта грамматика описывает язык булевых формул с переменными a, b, c и логическими операциями Ú, Ù, Ø. Выведем в данной грамматике формулу

f = (ā Ù b Ú c) Ù (a Ú b).

(I) ® (I Ù I) ® ((I Ú I) Ù I)) ® (((I Ù I) Ú I) Ù I) ® (((I Ù I) Ú I) Ù (I Ú I)) ®

® (((ØI Ù I) Ú I) Ù (I Ú I)) ® (((Øa Ù I) Ú I) Ù (I Ú I)) ® (((Øa Ù b) Ú I) Ù (I Ú I)) ®

® (((Øa Ù b) Ú c) Ù (I Ú I)) ® (((Øa Ù b) Ú c) Ù (a Ú I)) ® (((Øa Ù b) Ú c) Ù (a Ú b)).

Следует отметить, что хотя порождающая грамматика и описывает процесс порождения цепочек языка L(G), но описание это не является алгоритмическим. В грамматике отсутствует одно из основных свойств алгоритма — детерминированность. То есть не фиксируется конкретный порядок применения правил подстановки. Так, в рассмотренном выше примере после цепочки (I Ù I) мы могли перейти не к цепочке ((I Ú I) Ù I)), а к цепочке (I Ù (I Ú I)).

 

Классы языков и грамматик

Грамматики и соответственно им и языки делятся на классы в зависимости от ограничений, которые определяются для правил. Среди множества классов выделим классы, рассмотренные Ноамом Хомским. Запишем правило в виде p: j®m .

Если для правил никаких ограничений нет, кроме одного – в слове j должен быть хотя бы один нетерминальный символ, то такие грамматики (так же как и языки) отнесём к классу 0 и назовём грамматиками (языками) с фразовой структурой.

Если слова имеют вид: j = j1 j2 j3, m=j1m1 j3, т.е. замена j2 на m1 произойдет только в том случае, если перед ним стоит j1, а после j3, т.е. зависит от контекста. Цепочки j1 и j3 образуют контексты (j1 –левый контекст, j3 – правый контекст). В частности, j2 может быть нетерминальным символом, а m1 – произвольным словом. Такие грамматики называются неукорачивающими. В них каждое следующее слово в цепочке не меньше предыдущего. Такие грамматики называются контекстными или грамматиками класса 1.

Если в правилах j – нетерминальный символ, а m – произвольное слово, то грамматика называется контекстно-свободной (КС-грамматикой) или грамматикой класса 2.

КС-грамматики широко используются при описании конструкций языков программирования. Синтаксис большинства известных языков программирования основан именно на КС-грамматиках.

И, наконец, грамматики, в правилах которых всегда j – нетерминальный символ, а m — или терминальный символ или пара символов, первый из которых нетерминальный, а второй — терминальный, называют леволинейными. Если в правилах m — или терминальный символ или пара символов, первый из которых терминальный, а второй — нетерминальный, то грамматики называются праволинейными. Показано, что оба эти класса грамматик эквивалентны, т.е. образуют один и тот же класс языков. Такие грамматики называют регулярными или автоматными или грамматиками класса 3.

Так же как и грамматики. соответствующие им языки называют контекстными, контекстно-свободными и автоматными.

 

Автоматные языки

Установим связь между грамматикой автоматного языка и соответствующим ему автоматом. Терминальными символами языка являются символы входного алфавита языка, т.е. V=Z.

Примем за нетерминальные символы языка имена состояний автомата. Но в этом случае аксиомой языка необходимо назвать те нетерминальные символы, которые сопоставлены заключительным состояниям. Но заключительных состояний может быть несколько, а аксиома в грамматике единственна. Чтобы преодолеть это несогласование, в терминальный словарь вводят ещё один символ (обозначим его g), который называют пустым символом. Все заключительные состояния автомата в графе переходов связывают с одним заключительным дугами, помеченными входным сигналом g, и предполагают, что эти переходы происходят без подачи какого-либо сигнала на вход автомата. Тогда это единственное состояние и определяется как соответствующее аксиоме (или цели) языка.

Пример. Грамматика языка представлена автоматом на рис.5.1.

 

Состояния 6 и 4 заданы как заключительные (отмечены символом звёздочка), состояние 0 – начальное. В состояние 3 автомат приходит тогда, когда слово не является словом языка.

Как видно из графа, слова abb, abab, abaaa¼ab, accb, acccb, bc, bccc будут словами языка; слова, начинающиеся с c, bb, ba, aa, bcb, словами языка не являются.

Правила грамматики этого языка можно определить следующим образом. Вначале для каждого заключительного состояния сопоставим каждой заходящей в него дуге пару <исходящее состояние> <имя переменной>. Так, в состояние 6 из состояния 5 приходит дуга, отмеченная переменной b. Этому будет соответствовать правило

p1: 6 ::=5b
Трём заходящим в вершину 4 дугам будут соответствовать правила

p2: 4::=1c

p3: 4::=5c

p4: 4::=2c

Затем для каждого состояния, кроме начального и тупикового, запишем подобные правила для каждой заходящей в них дуги. Например, для состояния 5 это будут правила

p5: 5::= 1b

p6: 5::= 4c

p6: 5::= 5a

При этом, если дуга исходит из начальной вершины, имя её не указывается, т.е. правило приобретает вид как для вершин 1, 2, 3

p7: 1::= a

p8: 2::= b

p9: 3::= c

Таким образом, приходим к следующему утверждению.

Теорема. В автоматных грамматиках правила всегда имеют вид A::= Bc или A::= c, где строчными символами обозначены терминальные, а прописными – нетерминальные символы.

Пример. Построим автомат, проверяющий правильность расстановки скобок в формулах. Правило имеет вид: при построении формулы в любой момент число закрывающих скобок должно быть не больше числа скобок открывающих, в конце формулы их число должно быть одинаковым. Пусть глубина вложения скобок не больше четырёх. Граф переходов автомата имеет вид
как на рис. 5.2.

                                  Рис.5.2

Обозначим как a любой символ в формуле, кроме скобок. Начальная вершина обозначена как вершина 1, конечная вершина имеет имя к. Символом о обозначена вершина для неправильно построенной формулы (она имеет лишнюю закрывающую скобку). Дуга (5, 0) отмечает, что глубина вложения скобок больше допустимых четырёх. Здесь предполагается, что содержимое скобок может быть пустым. Символьное содержание текста не контролируется.

Этому автомату соответствует следующая грамматика.

Терминальный словарь содержит символы для построения формул, в том числе знаки операций и скобки.

Нетерминальный словарь может быть

N={<формула>, <непол_фор1>, <непол_фор2>, <ошибка>, <непол._фор3>, <непол._фор4>, <символ>, <слово>, }.

Здесь в качестве вспомогательных (нетерминальных) символов определены: <символ> – любой символ терминального словаря, <непол_форi> (i=1,2,3,4) определяет уровень вложенности. Формула просматривается сначала, при открывании очередной скобки уровень увеличивается на единицу, при закрывании – уменьшается на единицу. Уровень вложенности по условию задачи не может быть больше четырёх. Символ <ошибка> определяет, что произошла ошибка: или число закрывающих скобок в формуле оказалось больше числа открывающих или глубина вложенности больше четырёх. 

Целью является символ <слово>, который может быть или правильной формулой или ошибкой.

Правила имеют вид.

p1: <слово>::= <формула>½<ошибка >

p2: <формула>::= < >½<непол_фор1>) ½<формула><символ>

p3: <непол_фор1>::= (½<непол_фор1><символ>½<непол_фор2>)

p4: <непол_фор2>::= <непол_фор1>(½<непол_фор2><символ>½
<непол._фор3>)

p5: <непол._фор3>::= <непол_фор2>(½<непол._фор3><символ>½
<непол._фор4>)

p6: <непол._фор4>::= <непол._фор3>(½<непол._фор4><символ>

p7: <символ>::= a½b½c½d½¼½Z½1½2½¼½0½+½-½(½)½¼

p8: <ошибка> ::= <непол._фор4> (½формула) ½<ошибка> <символ>.

Здесь формулой может быть пустое слово или композиция символов, в которой число открывающих и закрывающих скобок совпадает. При этом внутри формулы нигде число отрывающих скобок не должно быть больше число закрывающих. На каждом уровне от первого до четвёртого, приход следующей открывающей скобки увеличивает на единицу глубину вложенности следующего текста (правила p3-p6). Закрывающая скобка этот уровень уменьшает (правила p2-p5).

К состоянию ошибки приходим (правило 8), если уровень вложенности превысил заданный (первый вариант правила 8) или число закрывающих скобок стало больше открывающих (второй вариант
правила 8). Последующий текст ошибку исправить не может (последний вариант в правиле 8).

 

Упражнения

Задан терминальный алфавит Vт ={a, b, c, d}, нетерминальный алфавит Vн={A,B,C}, аксиомой языка является символ C. Построить описание автомата для следующей грамматики.

Вариант 1.  P={ p1: С::=aB; p2: C::=aA; p3::B=dA; p4: A::=aB; p5: A::= a}. Вариант 2.  P={p1: С::=aB; p2: C::=bA ; p3::B::=bA; p4: A::= cB; p5: A::= a; p6: B::=d}. Вариант 3.  P={p1: С::=aB; p2: C::=bA ; p3: C::=aA; p3::B::=bA; p4: A::= cB; p5: A::= a; p6: B::=d}.

Вариант 4. P={p1: С: ::=aB; p2: C::=cB ; p3: C::=aA; p3::B::=aA; p4: B::= bB; p5: A::= dA; p6: A::=d. p7: B::=b}. Вариант 5.     P={ p1:С::=aB; p2: C::=bB ; p3: B::=aA; p3::B::=aB; p4: B::= bB; p5: A::= dA; p6: A::=d. p7: B::=b h8: A::=a}.

 

 

Библиографический список

1. Карпов Ю.Г. Теория автоматов / Ю.Г. Карпов СПб.: Изд.дом ПИТЕР, 2002.

2. Богомолов А.М. Алгебраические основы теории дискретных систем / А.М. Богомолов, В.Н. Салий.  М.: Наука, 1998.

3. Баранов С.И. Синтез микропрограммных автоматов / С.И. Баранов М.: Энергия, 1985.

4. Поспелов Д.А. Логические методы анализа и синтеза схем / Д.А. Поспелов М.: Энергия, 1974.

5. Мелихов А.Н. Ориентированные графы и конечные автоматы / А.Н. Мелихов М: Наука, 1971.

 

Учебное издание

 

Валерий Петрович Битюцкий,

Игорь Васильевич Хмелевский

 

ПРОЕКТИРОВАНИЕ АВТОМАТОВ

 

 

Редактор  Н.П.Кубыщенко

Компьютерная верстка Битюцкого В.П.

 

 

ИД №06263 от 12.11.2001 г.

Подписано в печать 24.01.2006                     Формат 60х84 1/16

Бумага типографская  Офсетная печать              Усл.печ.л 5,41

Уч.-изд.л. 5,8               Тираж            Заказ                Цена “С”

 

Редакционно-издательский отдел ГОУ ВПО УГТУ-УПИ

620002, Екатеринбург, Мира, 19

ООО «Издательство УМЦ УПИ, 620002, Екатеринбург, Мира, 17

 

 

ПРОЕКТИРОВАНИЕ АВТОМАТОВ

 

Федеральное агентство по образованию

ГОУ ВПО «Уральский государственный технический университет -УПИ»

 

В.П.Битюцкий

И.В.Хмелевский

 

ПРОЕКТИРОВАНИЕ АВТОМАТОВ

Учебное пособие

 

Научный редактор– проф., д-р техн.наук В.И.Кузякин

 

 

 

 

 

Екатеринбург

2006

 

 

УДК 519.713.001.63

ББК 32.815-02

Б66

 

Р е ц е н з е н т ы

Кафедра информатики Уральского  государственного горного университета (зав.кафедрой проф., д-р техн. наук М.Б.Носырев);

доц., канд.техн.наук Г.Б.Захарова (УрО РАН).

 

 

Авторы: В. П. Битюцкий И.В.Хмелевский

Б66 Проектирование автоматов: учебное пособие /В.П. Битюцкий, И.В.Хмелевский. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 93 с.

ISBN 5-318-00537-3

 

 

Приводятся основные понятия и утверждения из теории абстрактных и структурных автоматов, вопросы их минимизации, композиции, декомпозиции и синтеза. Решение задачи проектирования автоматов доведено до синтеза схемы автомата в заданном базисе.

 Рассмотрены вопросы учёта временных характеристик элементов, гонки и состязания в сетях, способы противогоночного кодирования состояний автомата.

Отдельный раздел посвящен автоматам-распознавателям, для чего рассмотрены формальные грамматики и языки, которые понимают автоматы.

 

 

Библиогр. : 5 назв. Табл. 50. Рис. 32.    

 

УДК 519.713.001.63

ББК 32.815-02

 

 

ISBN 5-318-00537-3                ÓГОУ ВПО «Уральский государственный

технический университет-УПИ»,   2006

Ó В.П. Битюцкий, И.В.Хмелевский 2006

 

Оглавление

Введение. 5

1. Абстрактные автоматы.. 7

1.1. Эквивалентность автоматов. 9

1.2. Минимизация автоматов. 13

1.2.1. Минимизация полностью определенного автомата. 13

1.2.2. Минимизация частичного автомата. 14

1.3. Композиция автоматов. 20

1.3.1. Параллельное соединение. 20

1.3.2. Последовательное соединение. 20

1.3.3. Соединение с обратной связью.. 21

1.3.4. Соединение в сеть. 21

1.4 Декомпозиция автомата. 24

1.4.1. Задача декомпозиции. 24

1.4.2. Разбиения со свойствами подстановки. 25

1.4.3. Метод декомпозиции. 27

1.5. Упражнения. 31

Эквивалентность автоматов. 31

Минимизация полностью определённого автомата. 33

Декомпозиция автоматов. 34

2. Структурные автоматы.. 37

2.1. Автоматная полнота и теорема В.М.Глушкова. 37

2.2. Гонки в автомате. 40

2.2.1. Кодирование состояний. 40

2.2.2. Понятие о гонках. Противогоночное кодирование. 40

2.3. Проектирование автомата. 42

2.4. Упражнение. 46

Кодирование. 46

Синтез автомата. 48

3. Синтез схем.. 49

3.1. Определения. 49

3.2. Функциональная полнота базиса. 50

3.2.1. Классы функций. 50

3.2.2. Монотонные функции. 50

3.2.3. Самодвойственные функции. 51

3.2.4. Линейные функции. 52

3.2.5. Функции, сохраняющие константу. 53

3.2.6. Функциональная полнота. 54

3.3. Топологические ограничения в схемах. 56

3.3.1. Плоские схемы.. 57

3.3.2. Ограничения на глубину связи в схеме. 58

3.4. Методы синтеза схем.. 62

3.4.1. Метод факторизации. 62

3.4.2. Метод декомпозиции. 62

3.4.3. Синтез схем в классическом базисе. 65

3.4.4. Синтез схем в монофункциональном базисе. 65

3.5. Упражнения. 67

Функциональная полнота. 67

Синтез схем.. 67

4. Эксперименты над автоматами. 69

4.1. Построение диагностических деревьев. 69

4.2. Диагностические и установочные эксперименты.. 70

4.2.1. Дерево преемников. 71

4.2.2. Диагностический эксперимент. 72

4.2.3. Установочный эксперимент. 76

4.3. Упражнения. 76

Диагностические эксперименты.. 76

Установочные эксперименты.. 78

5. Формальные грамматики. 78

5.1. Языки и порождающие их грамматики. 78

5.2. Примеры фрагментов описаний в языках программирования. 82

5.3. Порождающая грамматика. 83

5.4. Классы языков и грамматик. 87

5.5. Язык, понимаемый устройством.. 87

5.6. Автоматные языки. 88

5.7. Упражнения. 92

Библиографический список. 92

 

 

Введение

Теория автоматов посвящена представлению преобразователей информации и связана с проектированием сложных вычислительных и управляющих систем. Глушков В. М. и Уитни У. высказали идею о том, что любую систему, поведение которой описывается алгоритмически, можно представить композицией управляющего и операционного уст-ройств. Первое из них является логически более сложным и для него используется автоматная модель (модель Мура-Миля). Примером может служить описание некоторой команды ЭВМ. Команда описывается алго-ритмом, элементарными операциями для которого служат операции над регистром (сдвиги, инвертирование), сумматором и другие. Алгоритму сопоставляется автомат управления выполнением команды. Этот автомат определяет порядок выполнения (инициализации) элемен-тарных операций. Регистры, сумматоры и другие образуют операционное устройство, в котором и выполняются элементарные операции.

Изучение автоматных моделей связано с реализацией (проектиро-ванием) и моделированием управляющих устройств в заданных базисах.

Второй областью, где используются автоматные модели, являются формальные языки. В частности, можно назвать проблему грамматиче-ского разбора фраз формального языка и проблему проверки правиль-ности конструкций языка. Здесь наиболее эффективный способ решения связан с использованием автоматных моделей.

Учебное пособие состоит из двух неравнозначных по объёму частей. В первой, включающей главы с 1-й по 4-ю, решаются вопросы проектирования автоматов-преобразователей. Подробно рассматрив-аются автоматы на абстрактном уровне, их минимизация, декомпозиция на связанные сетью более простые автоматы, переход к структурному автомату и его синтез. Решение задачи доведено до построения схемы из заданных элементов базиса.

Отдельными разделами в этой части стоят вопросы обеспечения корректной работы автомата при учёте разбросов временных характеристик элементов базиса – противогоночное кодирование автомата и эксперименты над автоматами.

Во второй части (глава 5) изучаются автоматы – распознаватели, которые предназначены для анализа формальных языков. Для этого приведены необходимые понятия из формальных языков и грамматик.

Изложение сопровождается поясняющими примерами и задачами, решение которых поможет более глубокому пониманию материала.

 

 

В стандарте специальности ВМКСС задачи профессиональной деятельности определены следующим образом:

инженер должен быть подготовлен к решению следующих профессиональных задач:

· определение целей проектирования объектов профессиональной деятельности, критериев эффективности проектных решений, ограничений;

· проектирование архитектуры аппаратно-программных комплексов и их компонентов;

· выбор средств вычислительной техники (ВТ), средств программирования и их применения для эффективной реализации аппаратно-программных комплексов;

· оценка надежности и качества функционирования объекта проектирования.

 Квалификационные требования.

Подготовка выпускника должна обеспечивать квалификационные умения для решения профессиональных задач:

· участие во всех фазах проектирования, разработки, изготовления и сопровождения объектов профессиональной деятельности;

· участие в разработке всех видов документации на программные, аппаратные и программно-аппаратные комплексы;

· использование современных методов, средств и технологии разработки объектов профессиональной деятельности.

Материал данного учебника должен стать базой для решения этих задач.

 

Абстрактные автоматы

Определение. Абстрактным автоматом Мили называется преобразователь, представимый пятёркой

S=<Z, W, A, l, d>,

где Z – входной алфавит {z1, z2, …, zr},

W – выходной алфавит {w1, w2,…, wp},

A  – алфавит состояний {a1, a2,…, at},

d– функция переходов AxZ® А,

l – функция выходов AxZ® W.

Если, кроме того, определено начальное состояние автомата a₀
(a₀ – символ из А), то говорят об инициальном  автомате Мили.

Семантика: автомат функционирует в дискретном времени. В лю-бой момент времени он находится в некотором состоянии a_i из множест-ва A, и на его вход поступает входной сигнал z_i из множества Z. В зави-симости от состояния и входного сигнала в следующий момент автомат переходит в новое состояние a_j, определяемое функцией перехода, a_j=d(a_i, z_i), при этом на его выходе формируется выходной сигнал
w=l(a_i, z_i) (рис.1.1). В инициальном автомате в начале функционирова-ния автомат находится в состоянии a₀ .

Автомат Мили представляется матрицей переходов и матрицей выходов, описывающими соответствующие функции.

Пример 1. Автомат задан на множествах входов Z={z1, z2, z3}, состояний A={a1, a2, a3, a4, a5, a6} и выходов W={w1, w2}. Его функционирование описывается матрицами переходов и выходов, приведёнными в табл.1.1 и 1.2.

 

Таблица 1.1

Таблица 1.2

a1

a2

a3

a4

a5

a6

a1

a2

a3

a4

a5

a6

z1

a3

a5

a6

a6

a1

a5

z1

w1

w1

w2

w1

w2

w1

z2

a1

a6

a4

a4

a4

a1

z2

w1

w1

w1

w1

w1

w1

z3

a5

a1

a3

a2

a5

a3

z3

w1

w1

w2

w2

w2

w1

Автомат Мили может быть также представлен в виде объединённой матрицы. В этом случае каждая клетка матрицы состоит из двух частей, в одной из которых записывается следующее состояние (функция d (ai, z)), во второй части – выход (функция l (ai, z)).

Таблица 1.3
	a1	a2	a3	a4	a5	a6
z1	a3w1	a5w1	a6w2	a6w1	a1w2	a5w1
z2	a1w1	a6w1	a4w1	a4w1	a4w1	a1w1
z3	a5w1	a1w1	a3w2	a2w2	a5w2	a3w1

Объединённая матрица представленного выше автомата показана в табл. 1.3.

Автомат Мили может быть описан в виде графа. Вершинам этого графа сопоставлены состояния, дугам – переходы. При этом на каждой дуге записывается значение входа, определяющего этот переход, и значение выхода на этом переходе. Эта пара вход-выход называется весом дуги. Для рассмотренного автомата граф имеет вид как на рис.1.2

 

 

Рис.1.2

Автоматом Мура называют автомат, в котором функция выходов зависит только от состояния, то есть для него функция выходов автомата: m: A®W.

Пример 2. Автомат Мура задан на тех же множествах, что и автомат в примере 1, а его функционирование описывает табл. 1.4.

В графе автомата Мура дуги взвешиваются только значением соответствующего входа, значение выходов приписываются его вершинам.

Таблица 1.4
	w a1	w1 a2	w2 a3	w1 a4	w2 a5	w1 a6
z1	a3	a5	a6	a6	a1	a5
z2	a1	a6	a4	a4	a4	a1
z3	a5	a1	a3	a2	a5	a3

Для приведённого автомата граф будет иметь вид как на рис.1.3

 

Рис.1.3

 

Реакция автомата в состоянии ai на входное слово z* определяется по таблицам переходов и выходов. Для последнего примера реакцией автомата в состоянии a2 на слово z1z2z1 будет слово w2w1w1.

 

Эквивалентность автоматов

 

Состояния автомата ai и aj называются эквивалентными, что обозначается как ai~aj, если для них имеет место: "z

1. l (ai, z)= l (aj, z),

2. d (ai, z)~ d(aj, z).

Свойства отношения эквивалентности состояний:

1. a_m ~ a_m, 2. a_m ~ a_n => a_n ~ a_m, 3. (a_m ~ a_k)&(a_n ~ a_k)Þ a_m ~ a_n.

Таким образом, это есть отношение эквивалентности в общепринятом теоретико-множественном смысле, и множество состояний разбивается на непересекающиеся классы состояний – классы эквивалентности.

Автоматы S=<Z, W, A, l, d>, и S1=<Z, W, A1, l1, d1>, называют эквивалентными, что обозначается как S ~S1, если ("аÎА $а1ÎА1, a ~ a1) &("а1ÎА1 $ аÎА, a1 ~ a).

 

Были введены две модели автоматов – автомат Мура и автомат Мили. Следующая теорема показывает, что эти модели равномощны, т.е. любой автомат можно реализовать в каждой из этих моделей.

Теорема.  Для любого автомата Мура существует эквивалентный ему автомат Мили и наоборот.

Доказательство теоремы построим на преобразовании автомата одного типа, описанного с помощью графа, в автомат другого типа.

Необходимость. Покажем, как для любого автомата Мура построить эквивалентный ему автомат Мили. Для этого достаточно перенести выходы автомата с вершин графа на входящие дуги графа.

Рассмотрим это на примере автомата Мура Sµ=<Z,W,A, l, d ,>, где А={a0, a1, a2, a3, a4}; Z={x1,x2,x3}; W={w1,w2}. Функции автомата представлены в виде графа на рис. 1.4. Результирующий автомат функционирует в соответствии с графом на рис.1.5. Полученный автомат эквивалентен исходному автомату по построению.

Достаточность. Покажем, что для любого автомата Мили можно построить эквивалентный ему автомат Мура. Для каждой вершины графа рассмотрим заходящие в неё дуги. Если эти дуги взвешены различными значениями выхода, то расщепим вершину таким образом, чтобы каждому значению выхода соответствовала своя вершина, и каждую дугу направим в свою вершину.

Пусть автомат Мили  S описан в виде графа на рис. 1.6. Рассмот-рим состояние a2, в которое заходят дуга (a0, a2), отмеченная выходом w1, и дуга (a3, a2), отмеченная выходом w3, и дуга (a1,a2), отмеченная выходом w2. Других заходящих дуг в эту вершину нет, значит расщепим вершину a2 в графе для автомата Мура на a2, которой сопоставим вы-ход w2 и куда направим дугу (a1, a2), вершину a1`, которой сопоставим

 

 

z2/w2

выход w1 и куда направим дугу (a0,a2`), и вершину a2``, куда направим дугу (a3,a2) и которой сопоставим выход w3. Выходные дуги для вновь введённых вершин будут те же, что и для исходной вершины. Таким образом, из вершин a2` и a2`` должны исходить дуги к тем же вершинам, что и из вершины  a2. 

Полученный автомат описан графом на рис. 1.7.     

 

	z2/w2

 

 

		Рис.1.6
			Рис.1.7

 

Очевидно, что автоматы S и S' эквивалентны по построению.

Модель автомата Мура проще, за простоту модели заплатили большим числом состояний.

Минимизация автоматов

 

Если состояния автомата эквивалентны, то они неразличимы между собой по реакции на любое входное слово. Автомат называется минимальным, если в нём нет эквивалентных состояний.

В предыдущем разделе введено понятие эквивалентности автоматов, позволяющее дать второе определение минимального автомата. Для автомата S минимальным автоматом называют автомат, имеющий минимальное число состояний среди множества автоматов, эквивалентных ему.

Задачу нахождения автомата, минимального заданному, называют задачей минимизации автомата.

 

12345678910Следующая ⇒

Поделиться: