Минимизация комбинационных схем
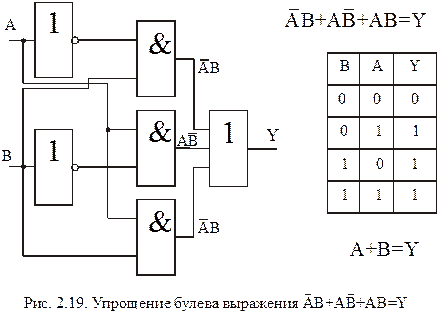 На рис.2.19 приведено логическое выражение, таблица истинности и схема, построенная по данному выражению. Вместе с тем, показанная таблица истинности соответствует функции ИЛИ с двумя входами (A+B=Y). Таким образом, среди множества схем, соответствующих одному логическому выражению встречаются схемы разной степени сложности. Данное обстоятельство приводит к мысли о том, что логические схемы можно минимизировать (т.е. получить схему минимальной сложности). С этой целью используют общие методы упрощения булевых выражений.
На рис.2.19 приведено логическое выражение, таблица истинности и схема, построенная по данному выражению. Вместе с тем, показанная таблица истинности соответствует функции ИЛИ с двумя входами (A+B=Y). Таким образом, среди множества схем, соответствующих одному логическому выражению встречаются схемы разной степени сложности. Данное обстоятельство приводит к мысли о том, что логические схемы можно минимизировать (т.е. получить схему минимальной сложности). С этой целью используют общие методы упрощения булевых выражений.  Существуют аналитические, табличные и графические приемы упрощения логических задач. Широкое распространение получил метод карт Карно. В 1953 г. Морис Карно опубликовал статью о разработанной им системе графического представления и упрощения булевых выражений. Карта Карно для двух переменных показана на рис.2.20. Четыре квадрата (1, 2, 3, 4, ) соответствуют четырем возможным комбинациям переменных в таблице истинности. Соответствие состояния выхода и квадрата карты Карно показано стрелками.
Существуют аналитические, табличные и графические приемы упрощения логических задач. Широкое распространение получил метод карт Карно. В 1953 г. Морис Карно опубликовал статью о разработанной им системе графического представления и упрощения булевых выражений. Карта Карно для двух переменных показана на рис.2.20. Четыре квадрата (1, 2, 3, 4, ) соответствуют четырем возможным комбинациям переменных в таблице истинности. Соответствие состояния выхода и квадрата карты Карно показано стрелками.

 Предположим, что необходимо составить карту Карно для логической задачи, проиллюстрированной на рис.2.19. Исходное булево выражение переписано еще раз на рис.2.21. Чтобы заполнить карту необходимо проставить единицы в тех квадратах, которым соответствуют произведения в исходном булевом выражении. Соответствие квадрата карты и произведения в исходном выражении показано стрелками. Процедура минимизации состоит в том, что соседние единицы объединяются в один контур по две, четыре или восемь единиц. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Каждый контур представляет собой новый член упрощенного булева выражения. На рис.2.22 показано построение контуров для карты с рис.2.21. В данной задаче получилось только два контура. Это означает, что упрощенное выражение будет состоять только из двух членов, связанных функцией ИЛИ. После того, как контуры выделены, определяют выражение для каждого контура. В нижнем контуре А встречается в комбинации с
Предположим, что необходимо составить карту Карно для логической задачи, проиллюстрированной на рис.2.19. Исходное булево выражение переписано еще раз на рис.2.21. Чтобы заполнить карту необходимо проставить единицы в тех квадратах, которым соответствуют произведения в исходном булевом выражении. Соответствие квадрата карты и произведения в исходном выражении показано стрелками. Процедура минимизации состоит в том, что соседние единицы объединяются в один контур по две, четыре или восемь единиц. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Каждый контур представляет собой новый член упрощенного булева выражения. На рис.2.22 показано построение контуров для карты с рис.2.21. В данной задаче получилось только два контура. Это означает, что упрощенное выражение будет состоять только из двух членов, связанных функцией ИЛИ. После того, как контуры выделены, определяют выражение для каждого контура. В нижнем контуре А встречается в комбинации с  и
и  . В соответствии с правилами булевой алгебры
. В соответствии с правилами булевой алгебры  и
и  дополняют друг друга и их можно опустить. Тогда в нижнем контуре останется один член А. Аналогично этому вертикально расположенный контур содержит
дополняют друг друга и их можно опустить. Тогда в нижнем контуре останется один член А. Аналогично этому вертикально расположенный контур содержит 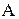 и
и  , которые можно также опустить, оставив только В. Оставшиеся А и В объединяют функцией ИЛИ, что приводит к выражению Y=А+В. На рис.2.22 стрелками показано построение упрощенного выражения.
, которые можно также опустить, оставив только В. Оставшиеся А и В объединяют функцией ИЛИ, что приводит к выражению Y=А+В. На рис.2.22 стрелками показано построение упрощенного выражения.
Последовательность действий при упрощении логических выражений с использованием карт Карно.
1. Записывается булево выражение в дизъюнктивной нормальной форме (ДНФ).
2. Наносятся единицы на карту Карно.
3. Объединяют соседние единицы контурами по две, четыре или восемь единиц.
4. Производят упрощение, исключая члены, дополняющие друг друга внутри контура.
5. Объединяют оставшиеся члены (по одному в каждом контуре) функцией ИЛИ.
6. Записывают полученное упрощенное булево выражение в ДНФ.
Рассмотрим исходное булево выражение
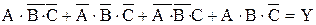 ,
,
приведенное на рис.2.23. На рис.2.23, а построена карта Карно для трех переменных и стрелками показано как она заполнена. Заполненная карта Карно повторена на рис.2.23, б, где показаны выделенные контуры. Нижний контур содержит

и

, вследствие чего

и

можно опустить. После этого в составе нижнего контура сохраняются лишь
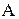
и

, которые дают член

. В верхний контур входят

и

, поэтому их опускают, в результате чего остается только член

. Конечное булево выражение в дизъюнктивной нормальной форме приобретает значительно более простой вид

.
Существенно, чтобы карта Карно была составлена именно так, как показано на рис.2.23. При этом при перемещении вниз по левой части карты, на каждом шагу изменяется лишь одна переменная. Если карту составить неправильно, она не будет давать ожидаемого эффекта.
Рассмотрим булево выражение 

представленное на рис.2.24, а. Ниже на рисунке показана карта Карно четырех переменных и стрелками показано как она заполняется. Полученная карта вторично изображена на рис.2.24, б. Группы из двух и четырех единиц объединены контурами. Нижний контур из двух единиц дает возможность опустить  и
и  . После этого в нем остается член
. После этого в нем остается член  . В верхнем контуре из четырех единиц попарно опускаются
. В верхнем контуре из четырех единиц попарно опускаются  и
и  ,
,  и
и  так, что в результате этого верхний контур дает член
так, что в результате этого верхний контур дает член  . Наконец эти члены объединяются символом операции ИЛИ, как показано на рис.2.24, б.
. Наконец эти члены объединяются символом операции ИЛИ, как показано на рис.2.24, б.
Отметим, что для упрощения булевых выражений с двумя, тремя и четырьмя переменными применяется общая процедура и одинаковые правила, и чем больше размеры объединяющих контуров, тем больше переменных можно опустить. В случае необходимости карта Карно может быть свернута в горизонтальный или вертикальный цилиндр или шар. Это дает возможность объединить клетки с единицами, находящиеся на противоположных границах или в углах карты.


 и
и  , вследствие чего
, вследствие чего  и
и  можно опустить. После этого в составе нижнего контура сохраняются лишь
можно опустить. После этого в составе нижнего контура сохраняются лишь 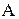 и
и  , которые дают член
, которые дают член  . В верхний контур входят
. В верхний контур входят  и
и  , поэтому их опускают, в результате чего остается только член
, поэтому их опускают, в результате чего остается только член  . Конечное булево выражение в дизъюнктивной нормальной форме приобретает значительно более простой вид
. Конечное булево выражение в дизъюнктивной нормальной форме приобретает значительно более простой вид  .
.