|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
|
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Элементы теории вероятностейСтр 1 из 3Следующая ⇒
Элементы теории вероятностей И математической статистики В юридической деятельности
Учебно-методический комплекс для студентов очной и заочной форм обучения (направление подготовки 030900 Юриспруденция (квалификация (степень) «Бакалавр»)
Воронеж 2011 Автор: Мишин Александр Владимирович, кандидат технических наук, доцент, заведующий кафедрой правовой информатики, информационного права и естественно-научных дисциплин Центрального филиала Российской академии правосудия.
Рецензенты: Стародубцев Виктор Сергеевич, доктор технических наук, профессор, заведующий кафедрой естественно-научных дисциплин филиала Российского государственного социального университета в г. Воронеже; Мистров Леонид Евгеньевич, доктор технических наук, доцент, профессор кафедры правовой информатики, информационного права и естественнонаучных дисциплин Центрального филиала Российской академии правосудия.
Учебно-методический комплекс составлен в соответствии с требованиями, установленными вузом по направлению подготовки 030900 Юриспруденция. Одобрен на заседании кафедры правовой информатики, информационного права и естественно-научных дисциплин Центрального филиала Российской академии правосудия от 24 июня 2011 г., протокол № 14. Утверждён учебно-методическим советом Центрального филиала Российской академии правосудия от 29 июня 2011 г., протокол № 8.
ÓРоссийская академия правосудия, 2011. ÓМишин А.В., 2011. СОДЕРЖАНИЕ
Требования к обязательному минимуму содержания модуля
Случайные события и операции над ними. Интерпретации вероятности. Простейшие комбинаторные конфигурации. Условные и безусловные вероятности событий. Априорные и апостериорные вероятности событий. Дискретные и непрерывные случайные величины. Основные законы распределения случайных величин. Числовые характеристики случайных величин. Вариационные ряды и способы их представления. Точечные и интервальные оценки параметров эмпирического распределения. Понятие статистической гипотезы. Содержание процедуры проверки гипотезы. Проверка гипотез о виде распределения. Введение
Элементы теории вероятностей и математической статистики в юридической деятельности - модуль вариативной части информационно-правового цикла, предметом изучения которого являются пути измерения и числовая характеристика степени объективной возможности появления какого-либо определённого события в массе однородных случайных событий, могущих повторяться неограниченное число раз. Модуль «Элементы теории вероятностей и математической статистики в юридической деятельности» играет важную роль в подготовке бакалавров. Его значение обусловлено тем, что методология теории вероятностей и математической статистики позволяет эффективно исследовать широкий круг социально значимых процессов и проблем в юридической деятельности, позволяет обучающемуся получить углубленные знания и навыки для успешной профессиональной деятельности и (или) для продолжения профессионального образования в магистратуре. Во всех случаях, когда применяются вероятностные методы исследования, их цель состоит в том, чтобы, минуя слишком сложное (и часто практически невозможное) изучение отдельного события, обусловленного очень большим количеством факторов, обратиться непосредственно к законам, управляющим массами случайных событий. Изучение этих законов позволяет не только осуществить научный прогноз в своеобразной области случайных событий, но в ряде случаев помогает целенаправленно влиять на ход случайных событий, контролировать их, ограничивать сферу действия случайности. Основная цель курса - сформировать у студентов знания, умения и навыки на уровне, обеспечивающем возможность самостоятельного применения математических методов для получения, обобщения и анализа информации о социально значимых проблемах и процессах. Достижению данной цели служат следующие задачи: 1) научить использовать статистический метод как систему принципов, требований, правил, руководствуясь которыми можно получать, обобщать и анализировать информацию о социально значимых проблемах и процессах; 2) показать применимость теории вероятностей и математической статистики для изучения закономерностей в случайных явлениях; 3) раскрыть фундаментальные понятия о случайных событиях и случайных величинах, количественных и качественных методах их оценки; 4) привить умения и навыки вычисления вероятностей случайных событий, числовых характеристик случайных величин, а также статистической обработки эмпирических данных; 5) раскрыть диалектическую связь социально значимых явлений и процессов со случайностью. Проектируемые результаты освоения курса: знать: предмет и фундаментальные понятия теории вероятностей и математической статистики; основные законы распределения вероятностей и числовые характеристики случайных величин; сущность статистического метода обработки эмпирических данных о социально значимых явлениях; уметь: применять вероятностный и статистический методы познания в юридической деятельности; использовать полученные знания для анализа социально значимых проблем и процессов, решения социальных и профессиональных задач; владеть: навыками отыскания безусловных и условных вероятностей случайных событий, числовых характеристик случайных величин; навыками графического представления эмпирических данных и точечной оценки параметров эмпирического распределения. Изучение дисциплины базируется на знаниях студентов по математике и информатике, полученных в средних образовательных учреждениях, и обеспечивает дисциплину «Судебная статистика». Структурно модуль состоит из двух разделов, в которых излагаются, соответственно, элементы теории вероятностей и математической статистики в объёме, необходимом специалисту юридического профиля. В первом разделе рассматриваются основные понятия теории вероятностей, простейшие комбинаторные конфигурации и правила вычисления вероятностей случайных событий. Формулируются основные способы задания дискретных и непрерывных случайных величин. Даются понятие и примеры законов распределения случайных величин. Излагаются правила вычисления основных характеристик случайных величин. Второй раздел охватывает понятийный аппарат математической статистики, способы представления выборочных данных, примеры точечных и интервальные оценок параметров эмпирического распределения, содержание процедуры статистической проверки гипотезы. Основной учебный материал выдаётся на практических занятиях. Полученные знания углубляются и расширяются в процессе самостоятельного изучения и подготовки контрольного задания (контрольной работы). Индивидуализация обучения на занятиях обеспечивается учётом уровня подготовки студентов, использованием персональных компьютеров (табличного процессора Microsoft Excel) для автоматизации сложных вычислений, контролем качества отработки практических заданий и контрольного задания (контрольной работы) каждым студентом. В этой связи занятия проводится в компьютерном классе в составе учебной подгруппы. Изучение модуля завершается сдачей зачёта. Виды учебной Работы (по учебному плану) | Форма обучения | ||||||||||||||||||||||||||||||||||||||||||||||
|
Очная |
Заочная | ||||||||||||||||||||||||||||||||||||||||||||||
| на базе среднего (полного) общего образования | на базе среднего профессионального юридического образования | на базе среднего (полного) общего образования | на базе среднего профессионального юридического образования | на базе высшего профессионального образования | |||||||||||||||||||||||||||||||||||||||||||
| Общая трудоёмкость | 36 | 36 | 36 | 36 | 36 | ||||||||||||||||||||||||||||||||||||||||||
| Аудиторные занятия | 18 | 18 | 4 | 6 | 4 | ||||||||||||||||||||||||||||||||||||||||||
| Лекции | |||||||||||||||||||||||||||||||||||||||||||||||
| Семинарские (практические) занятия | 18 | 18 | 4 | 6 | 4 | ||||||||||||||||||||||||||||||||||||||||||
| Самостоятельная работа | 14 | 14 | 28 | 26 | 28 | ||||||||||||||||||||||||||||||||||||||||||
| НИРС | 4 | 4 | 4 | 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||
| Контрольное задание | 1 | 1 | |||||||||||||||||||||||||||||||||||||||||||||
| Контрольная работа | 1 | 1 | 1 | ||||||||||||||||||||||||||||||||||||||||||||
| Форма итогового контроля | Зачёт | ||||||||||||||||||||||||||||||||||||||||||||||
Тематические планы
ТЕМАТИЧЕСКИЙ ПЛАН
(разделы дисциплины и темы занятий)
для студентов очной формы обучения
на базе среднего (полного) общего образования
Номера
И наименование
Разделов и тем
Общая трудоёмкость
Аудиторные занятия
НИРС
I семестр
Номера
И наименование
Разделов и тем
Общая трудоёмкость
Аудиторные занятия
НИРС
I семестр
Номера
И наименование
Разделов и тем
Общая трудоёмкость
Аудиторные занятия
НИРС
Семестр
Семестр
Тематический план
(разделы дисциплины и темы занятий)
для студентов заочной формы обучения
на базе среднего профессионального юридического образования
|
Номера И наименование Разделов и тем |
Общая трудоёмкость |
Аудиторные занятия |
НИРС | ||||||||||
| лекции | семинары | лабораторные работы | практические занятия | групповые занятия | курсовые работы (проекты) | контрольные работы | теоретические конференции | зачёты | Самостоятельная работа | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|
Семестр Семестр | |||||||||||||
| Тема № 9. Статистическая проверка гипотез | 2 | 2 | 2 | ||||||||||
| Контрольная работа | 12 | 8 | 4 | ||||||||||
| Форма итогового контроля – зачёт | 2 | 2 | |||||||||||
| Всего за 1 семестр | 16 | 2 | 2 | 10 | 4 | ||||||||
| Всего по курсу | 36 | 6 | 6 | 26 | 4 | ||||||||
Тематический план
(разделы дисциплины и темы занятий)
для студентов заочной формы обучения
на базе высшего профессионального образования
|
Номера И наименование Разделов и тем |
Общая трудоёмкость |
Аудиторные занятия |
НИРС | ||||||||||
| лекции | семинары | лабораторные работы | практические занятия | групповые занятия | курсовые работы (проекты) | контрольные работы | теоретические конференции | зачёты | Самостоятельная работа | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|
Семестр Семестр | |||||||||||||
| Тема № 9. Статистическая проверка гипотез | 2 | 2 | 2 | ||||||||||
| Контрольная работа | 14 | 10 | 4 | ||||||||||
| Форма итогового контроля – зачёт | 2 | 2 | |||||||||||
| Всего за 1 семестр | 18 | 2 | 2 | 12 | 4 | ||||||||
| Всего по курсу | 36 | 4 | 4 | 28 | 4 | ||||||||
Программа курса
Вариант 3
1. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трёх цифр. Сколько таких чисел можно составить, если повторение цифр в числах запрещено?
2. Среди 17 студентов группы, из которых 8 девушек, разыгрывается 7 пригласительных билетов. Какова вероятность того, что среди обладателей билетов окажутся 4 девушки?
3. В мастерской имеется три мотора. Вероятность того, что мотор работает с полной нагрузкой, равна 0,6. Найти вероятность того, что хотя бы один из трёх моторов работает с полной нагрузкой.
4. Путешественник может купить билет в одной из трёх касс железнодорожного вокзала. Вероятность того, что он направился к первой кассе, равна 0,4, ко второй - 0,5, к третьей - 0,1. Вероятности того, что билетов уже нет в кассах примерно такие: в первой кассе - 0,2, во второй - 0,3, в третьей - 0,15. Путешественник обратился в одну из касс и получил билет. Определить вероятность того, что он направился к первой кассе.
5. Закон распределения случайной величины X задан таблицей:
| х i | -2 | -1 | 1 | 3 | 5 | 7 |
| р i | 0,15 | 0,25 | 0,1 | 0,1 | 0,2 | 0,2 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
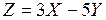, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 4; М Y = 1; DX = 3; DY = 2.
7. Среднее квадратическое отклонение ошибок измерения дальности радаром равно 25 м, а систематическая ошибка отсутствует. Определить вероятность получения ошибки измерения дальности, по абсолютной величине, не превосходящей 20 м.
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 11-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,9.
Вариант 4
1. Бросают одновременно три монеты и наблюдают за выпадением герба или цифры на верхних гранях каждой монеты. Сколько различных исходов опыта возможно?
2. В корзине находятся 5 красных и 4 синих мяча. Из корзины наудачу вынимают два мяча. Какова вероятность, что они оба окажутся красными?
3. При изготовлении изделия работают последовательно трое рабочих. Качество изделия при передаче его от одного рабочего к другому не проверяется. Первый рабочий допускает брак с вероятностью 0,1, второй - с вероятностью 0,2 и третий - с вероятностью 0,1. Найти вероятность того, что при изготовлении изделия будет допущен брак.
4. Противник применяет самолёты пяти типов. Известно, что на данном участке фронта сосредоточено примерно равное число самолётов каждого типа. Вероятности сбить самолёт при проходе над оборонительной зоной соответственно равны для них 0,4; 0,3; 0,2; 0,5; 0,1. Самолёт противника, прорывавшийся через оборонительную зону, сбит. Чему равна вероятность того, что это самолёт второго типа?
5. Закон распределения случайной величины X задан таблицей:
| х i | -5 | -3 | 1 | 2 | 5 | 6 |
| р i | 0,1 | 0,25 | 0,15 | 0,15 | 0,2 | 0,15 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 5; М Y = 4; DX = 1; DY = 4.
7. Рост взрослых женщин является случайной величиной, распределенной по нормальному закону. Пусть математическое ожидание её равно 164 см, а дисперсия – 25 см2. Вычислить вероятность того, что хотя бы одна из двух наудачу выбранных женщин будет иметь рост от 162 до 168 см.
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 16-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,95.
Вариант 5
1. Сколькими способами могут 8 человек встать в очередь в театральную кассу?
2. Из тридцати карточек с буквами русского алфавита наугад выбирают пять. Какова вероятность, что эти карточки в порядке выхода составят слово «право»?
3. Стрелок, стреляет три раза по удаляющейся мишени. Вероятность попадания в мишень в начале стрельбы равна 0,7, а после каждого выстрела она уменьшается на 0,1. Вычислить вероятность хотя бы одного попадания в мишень.
4. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить норму мастера спорта равна: для лыжника 0,9, для велосипедиста 0,8 и для бегуна 0,7. Найти вероятность того, что спортсмен, вызванный наудачу, выполнит норму мастера спорта.
5. Закон распределения случайной величины X задан таблицей:
| х i | -6 | -4 | 0 | 3 | 5 | 6 |
| р i | 0,1 | 0,05 | 0,35 | 0,15 | 0,2 | 0,15 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 5; М Y = 4; DX = 2; DY = 5.
7. Размер диаметра втулок можно считать нормально распределенной случайной величиной с математическим ожиданием 2,5 см и дисперсией 0,0001 см2. Найти вероятность того, что диаметр наудачу взятой втулки лежит между 2,48 см и 2,515 см.
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 21-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,98.
Вариант 6
1. Сколько существует пятизначных чисел, которые начинаются цифрой 2 и оканчиваются цифрой 4?
2. Из колоды в 52 карты берётся наугад четыре карты. Найти вероятность того, что среди этих четырёх карт будут представлены все четыре масти.
3. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,9. Найти вероятность того, что из трёх проверенных изделий только два высшего сорта.
4. На склад поступает продукция трёх фабрик. Причём продукция первой фабрики составляет 30%, второй - 35% и третьей - 35%. Известно также, что средний процент нестандартных изделий для первой фабрики равен 5%, для второй - 2% и для третьей - 1%. Наудачу взятое изделие оказалось стандартным. Какова вероятность того, что оно произведено на первой фабрике?
5. Закон распределения случайной величины X задан таблицей:
| х i | -4 | -1 | 1 | 2 | 5 | 6 |
| р i | 0,2 | 0,25 | 0,05 | 0,25 | 0,15 | 0,1 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 7; М Y = 2; DX = 5; DY = 1.
7. Производится одно измерение прибором, имеющим систематическую ошибку 5 м и среднее квадратическое отклонение 6 м. Какова вероятность того, что измеренное значение будет отклоняться от истинного не более чем на 15 м?
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 26-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,99.
Вариант 7
1. Сколько чисел, заключающихся между 1000 и 9999, содержат цифру 3?
2. Из коробки, содержащей 14 разноцветных карандашей, в том числе 2 жёлтых и 2 фиолетовых, наудачу вынимается карандаш. Найти вероятность того, что этот карандаш не будет ни жёлтым, ни фиолетовым.
3. Три спортсмена участвуют в отборочных соревнованиях. Вероятности зачисления в сборную команду первого, второго и третьего спортсменов соответственно равны 0,8, 0,7 и 0,6. Найти вероятность того, что хотя бы один из спортсменов попадёт в сборную.
4. Среди поступающих на сборку деталей с первого автомата - 1% бракованных, со второго автомата - 2%, с третьего - 2%, с четвёртого - 3%. Производительности автоматов относятся, как 4 : 3 : 2 : 1 соответственно. Взятая наудачу деталь оказалась стандартной. Найти вероятность того, что её изготовил четвёртый автомат.
5. Закон распределения случайной величины X задан таблицей:
| х i | -5 | -3 | 1 | 2 | 5 | 6 |
| р i | 0,1 | 0,25 | 0,15 | 0,15 | 0,2 | 0,15 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
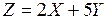, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 5; М Y = 4; DX = 3; DY = 4.
7. Предполагая, что дальность полета снаряда распределена по нормальному закону, со средним квадратическим отклонением 40 м, найти вероятность того, что снаряд даст перелет от 60 до 80 м, если известно, что прицеливание систематических ошибок не имеет.
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 31-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,9.
Вариант 8
1. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые не начинаются с цифры пять?
2. В круг вписан равносторонний треугольник. Найти вероятность того, что точка, брошенная наудачу в круг, окажется внутри треугольника.
3. При изготовлении детали заготовка должна пройти три операции обработки. Вероятность брака в первой операции равна 0,02, во второй - 0,03, в третьей - 0,01. Найти вероятность изготовления стандартной детали, считая появление брака в каждой операции независимыми событиями.
4. Одинаковые детали изготовляются на трёх станках: 25% на первом, 30% на втором и 45% на третьем. В продукции станков брак составляет соответственно 3%, 2%, 1%. Какова вероятность, что случайно взятая деталь окажется стандартной?
5. Закон распределения случайной величины X задан таблицей:
| х i | -6 | -3 | 0 | 1 | 4 | 5 |
| р i | 0,1 | 0,05 | 0,35 | 0,25 | 0,2 | 0,05 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 7; М Y = 8; DX = 3; DY = 2.
7. Случайная величина Х распределена нормально с математическим ожиданием, равным 10. Вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (4; 16), равна 0,8664. Найти среднее квадратическое отклонение этой случайной величины.
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 36-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,95.
Вариант 9
1. Сколькими способами можно рассадить 5 мужчин и 5 женщин за круглым столом так, чтобы два лица одинакового пола не сидели рядом?
2. В корзине 4 красных, 6 синих и 7 жёлтых шаров. Из корзины вынули два шара. Найти вероятность того, что один из них окажется красным, а второй – синим.
3. Производится три выстрела по движущейся мишени. Вероятности попадания при первом, втором, третьем выстрелах соответственно равны 0,7, 0,6, 0,5. Определить вероятность не менее двух попаданий в мишень.
4. Получены три партии изделий одного образца. В первой партии – 10% бракованных изделий, а в двух других - двадцатая часть. Из произвольно выбранной партии извлечено бракованное изделие. Найти вероятность того, что оно извлечено из партии с наибольшим процентом брака.
5. Закон распределения случайной величины X задан таблицей:
| х i | -2 | -1 | 0 | 3 | 4 | 6 |
| р i | 0,15 | 0,1 | 0,3 | 0,15 | 0,2 | 0,1 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 4; М Y = 6; DX = 3; DY = 2.
7. Прибором, имеющим среднеквадратическую ошибку 20 кг/см2 и систематическую ошибку 7 кг/см2, производят измерение максимального напряжения в станине. Какова вероятность, что ошибка измерения не превзойдет по абсолютной величине 5 кг/см2?
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 41-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,98.
Вариант 10
1. У филателиста есть восемь разных канадских марок и десять марок США. Сколькими способами он может отобрать три канадских, три американских марки и наклеить их в альбом на шесть пронумерованных мест?
2. В круг вписан квадрат. Найти вероятность того, что точка, брошенная наудачу в круг, окажется внутри квадрата.
3. Вероятность ошибки в ответе на каждый вопрос для данного студента равна 0,1. Какова вероятность, что студент сделает первую ошибку при ответе на третий вопрос?
4. В команде стрелков из 10 человек 3 мастера спорта, 4 спортсмена первого разряда и 3 спортсмена второго разряда. Вероятность попадания при одном выстреле для мастера спорта равна 0,95, для стрелка первого разряда - 0,9 и для стрелка второго разряда - 0,8. Какова вероятность того, что наудачу выбранный стрелок поразит цель?
5. Закон распределения случайной величины X задан таблицей:
| х i | -1 | 0 | 1 | 2 | 5 | 6 |
| р i | 0,05 | 0,25 | 0,25 | 0,2 | 0,15 | 0,1 |
Построить многоугольник распределения вероятностей величины X. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение данной случайной величины.
6. Найти математическое ожидание и дисперсию случайной величины 
, если известны математические ожидания и дисперсия случайных величин Х и Y: МХ = 5; М Y = 4; DX = 2; DY = 7.
7. Размер цилиндра деталей является случайной величиной, распределенной по нормальному закону с математическим ожиданием 5 см и дисперсией 0,81 см2. Найти вероятность того, что диаметр наудачу взятой детали лежит между 4 см и 7 см.
8. В таблице П. 3.2 (приложение 3) приведена последовательность случайных значений оцениваемого параметра. Сделайте выборку (n = 60), начиная с 46-го значения. Возьмите в качестве интервалов группировки интервалы (-3; -2), (-2; -1), (-1; 0), (0; 1), (1; 2), (2; 3) и напишите таблицу эмпирического распределения для этих интервалов. Постройте гистограмму, полигон, эмпирическую функцию распределения. Сделайте вывод о виде закона распределения оцениваемого параметра.
9. Используя таблицу эмпирического распределения, полученную при выполнении задания 8, найдите эмпирические среднее, дисперсию и среднеквадратическое отклонение оцениваемого параметра.
10. Используя точечные оценки (эмпирического среднего и дисперсии) оцениваемого параметра, полученные при выполнении задания 9, определите доверительный интервал для математического ожидания (при неизвестном среднеквадратическом отклонении) генеральной совокупности с уровнем доверия 0,99.
Примерный перечень вопросов для проведения рубежной аттестации
1. Определение случайного события.
2. Определение пространства элементарных исходов.
3. Какие случайные события называются противоположными? Какие – несовместными?
4. Когда случайные события образуют полную группу событий?
5. Содержание операций над случайными событиями.
6. Определение вероятности случайного события.
7. Каков диапазон численного значения вероятности любого события?
8. Каково правило вычисления вероятности суммы двух произвольных случайных событий?
9. Возможные интерпретации понятия вероятности.
10. В каких случаях применим классический способ вычисления вероятностей случайных событий? В каких случаях – геометрический и статистический способы?
11. Условия применения в комбинаторике правила суммы.
12. Условия применения в комбинаторике правила произведения.
13. Определение факториала числа.
14. Каково содержание и число размещений с повторениями?
15. Каково содержание и число размещений без повторений?
16. Как вычислить число перестановок без повторений?
17. Каково содержание и число сочетаний из n по m?
18. Как вычислить число перестановок с повторениями?
19. Какие события называются зависимыми?
20. Сформулируйте теорему умножения вероятностей.
21. Что означает и как вычисляется условная вероятность события?
22. Какие события называют независимыми?
23. Чему равна вероятность произведения двух независимых событий?
24. Какие события называются независимыми в совокупности? Как вычисляется вероятность произведения таких событий?
25. Каковы условия применения формулы Бернулли для вычисления вероятностей событий?
26. Какие события принято называть гипотезами?
27. Что означает несовместность событий?
28. В каком случае события образуют полную группу событий?
29. Приведите формулу полной вероятности и поясните условия её возможного применения.
30. Сформулируйте постановку задачи отыскания апостериорных вероятностей гипотез.
31. Каким образом можно рассчитать апостериорные вероятности гипотез?
32. Какие величины называются случайными?
33. Какими параметрами характеризуются случайные величины?
34. Каково содержание понятия «функция распределения вероятностей случайной величины»?
35. Каковы основные свойства функции распределения?
36. Какие случайные величины называются дискретными?
37. Каковы свойства функции распределения дискретной случайной величины?
38. Какие случайные величины называются непрерывными?
39. Какова особенность функции распределения непрерывной случайной величины?
40. Что понимается под плотностью распределения вероятностей случайной величины?
41. Каковы основные свойства плотности распределения вероятностей случайной величины?
42. Каково содержание понятия «математическое ожидание случайной величины»? Каковы свойства математического ожидания?
43. Поясните содержание понятий «мода» и «медиана» случайной величины.
44. Каково содержание понятия «дисперсия случайной величины»? Каковы свойства дисперсии?
45. Каково содержание понятия «среднеквадратическое отклонение случайной величины»? Каковы его свойства?
Примеры тестовых заданий
1. Число способов, которыми можно разложить в ряд шесть цветных фломастеров, равно …
£ 6
£ 36
R 720
£ 120
2. Число различных слов, которые можно составить, переставляя буквы в слове "перепел", равно …
£ 7
£ 42
R 420
£ 5040
3. В урне находится 5 белых шаров, 3 красных и 4 зелёных шара одинакового размера. Из урны извлекаются два шара наугад. Событие А – будут извлечены два белых шара. Вероятность события А равна …
£ 1/6;
£ 5/12;
£ 1/11;
R 5/33.
4. Из судебных дел прокурор отбирает дела, подлежащие прокурорскому надзору. Вероятность того, что наудачу взятое дело подлежит прокурорскому надзору, равна 0,4. Вероятность того, что из трёх проверенных дел только два подлежат прокурорскому надзору, равна …
R 0,288
£ 0,66
£ 0,096
£ 0,2
5. В адвокатской конторе приём граждан ведут три независимо работающих адвоката. Некто пришел на юридическую консультацию. Вероятность того, что первый адвокат будет готов к приёму, равна 0,6, второго - 0,7; третьего - 0,8. Вероятность того, что консультация будет предоставлена сразу (не придётся ожидать, пока кто-либо из адвокатов будет свободен), равна …
R 0,976
£ 0,624
£ 0,75
£ 0,336
6. К характеристикам рассеивания значений случайной величины относятся:
£ математическое ожидание
£ мода
£ медиана
R дисперсия
R среднеквадратическое отклонение
Литература*
Основная литература:
1*. Мишин А.В. Информатика и математика: Математика [Текст]: Учебное пособие / А.В. Мишин, Л.Е. Мистров, А.Ю. Кузьмин. – Воронеж: Центральный филиал Российской академии правосудия, 2006. – 174 с.
Дополнительная литература:
2*. Турецкий В.Я. Математика и информатика [Текст]: Учебник / В.Я. Турецкий. – 3-е изд., испр. и доп. – М.: ИНФРА-М, 2004. – 560 с.
3*. Квачко В.Ю. Математика для юристов [Текст]: Курс лекций / В.Ю. Квачко, В.Т. Королев, В.В. Радионов. – М.: Российская академия правосудия, 2004. – 179 с.
4. Гмурман В.Е. Теория вероятностей и математическая статистика [Текст]: учебное пособие для вузов / В.Е. Гмурман. – 6-е изд., стереотип. – М.: Высш. шк., 1998. – С. 187-207.
5*. Мишин А.В.
| |
6*. Математика [Текст]: справочник школьника и студента / Б. Франк, В. Шульц, В. Титц, Э. Вармут; пер. с нем. В.А. Чуянова. – 3-е изд., стереотип. – М.: Дрофа, 2003. – 368 с.
7*. Математика [Текст]: Энциклопедия / под ред. Ю.В. Прохорова. – М.: Большая Российская Энциклопедия, 2003. – 845 с.
Вопросы для подготовки к зачёту
1. Случайное событие. Виды случайных событий.
2. Пространство элементарных исходов. Правило его формирования.
3. Виды и содержание операций над случайными событиями.
4. Вероятность случайного события. Аксиомы, которым она удовлетворяет.
5. Правило вычисления вероятности суммы двух произвольных случайных событий.
6. Возможные интерпретации понятия вероятности.
7. Правило суммы в комбинаторике.
8. Правило произведения в комбинаторике.
9. Факториала числа: понятие и правило вычисления.
10. Число размещений с повторениями: понятие и правило вычисления.
11. Число размещения без повторений: понятие и правило вычисления.
12. Число перестановок без повторений: понятие и правило вычисления.
13. Число сочетаний: понятие и правило вычисления.
14. Число перестановок с повторениями: понятие и правило вычисления.
15. Теорема умножения вероятностей.
16. Условная вероятность события: понятие и правило вычисления.
17. Вероятность произведения двух независимых событий.
18. Формула Бернулли и условия её применения для вычисления вероятностей событий.
19. Какие события принято называть гипотезами?
20. Независимость и несовместность случайных событий.
21. Формула полной вероятности и условия её возможного применения.
22. Постановка задачи отыскания апостериорных вероятностей гипотез.
23. Формула Байеса и условия её возможного применения.
24. Случайные величины. Типы случайных величин.
25. Функция распределения вероятностей случайной величины и её основные свойства.
26. Плотность распределения вероятностей случайной величины и её основные свойства.
27. Математическое ожидание случайной величины и его свойства.
28. Понятия «мода» и «медиана» случайной величины.
29. Дисперсия случайной величины и её свойства.
30. Среднеквадратическое отклонение случайной величины и его свойства.
31. Определение степени зависимости между случайными величинами.
32. Коэффициент корреляции и его значение для анализа зависимости между случайными величинами.
33. Содержание выборочного метода и метода сплошных наблюдений.
34. Определение понятий «генеральная совокупность», «выборка», «статистический ряд», «вариационный ряд», «размах вариационного ряда».
35. Репрезентативность выборки и основные условия её обеспечения при статистических исследованиях.
36. Содержание табличного способа представления выборки.
37. Гистограмма, полигон» и кумулята. Правила их графического представления для выборки.
38. Постановка задачи точечной оценки параметров выборки.
39. Правила вычисления эмпирической средней, дисперсии и среднеквадратического отклонения.
40. Постановка задачи интервальной оценки параметров выборки.
41. Доверительная вероятность и доверительный интервал. Взаимосвязь между ними.
42. Постановка задачи статистической проверки гипотез.
43. Возможные ошибочные выводы при статистической проверке гипотез.
44. Бросается игральная кость. Событие А заключается в том, что выпадет более 2 очков, событие В - нечётное число очков. Указать: 1) пространство элементарных исходов; 2) достоверное и невозможное события, 3) содержание событий, полученных при выполнении следующих операций: А + В, А×В, А - В, В – А.
45. Три раза подбрасывается монета. Обозначим символом Г выпадение при одном бросании герба, Р - решки. Событие А заключается в том, что выпадет не менее одного герба, событие В - выпала ровно одна решка. Указать: 1) пространство элементарных исходов; 2) достоверное и невозможное события, 3) содержание событий, полученных при выполнении следующих операций: А + В, А×В, А - В.
46. В составе суда работают судьями: 5 мужчин и 4 женщины. На рассмотрение суда поступают 6 исковых заявлений, которые случайным образом распределяются между судьями. Найти вероятность того, что 3 иска попадут судьям-женщинам.
47. Студент озабочен предстоящими зачётами по математике и теории государства и права. По его мнению, вероятность того, что он сдаст теорию государства и права, равна 0,8, зачёт по математике - 0,6; вероятность того, что он сдаст, по крайней мере, один зачёт равна 0,9. Найти вероятность того, что он сдаст оба зачёта.
48. Внутрь круга радиуса R = 10 см наудачу брошена точка. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от её расположения относительно круга. Найти вероятность того, что точка окажется внутри помещённого в круг квадрата со сторонами а = 5 см.
49. Студент пришёл сдавать зачёт, зная из 70 вопросов только 50. Условия приёма зачёта: правильный ответ на первый или (в случае отказа отвечать на первый вопрос) второй вопрос. Какова вероятность того, что студент сдаст зачёт?
50. Два человека стреляют по одной и той же мишени. Один обычно попадает 8 раз из 10, а второй 7 раз из 10. Какова вероятность того, что цель будет поражена?
51. К двум исковым заявлениям, подлежащих рассмотрению судьёй, секретарь суда доложил иск уголовно-правового характера. Найти вероятность того, что первый наудачу взятый судьёй иск окажется иском уголовно-правового характера, если равновозможны все предположения о характере первоначальных исков.
52. Из судебных дел прокурор отбирает дела, подлежащие прокурорскому надзору. Вероятность того, что наудачу взятое дело подлежит прокурорскому надзору, равна 0,1. Какова вероятность того, что из пяти проверенных дел только два подлежат прокурорскому надзору?
53. 30% граждан, обратившихся в суд, принадлежат первой социальной группе, 40% - второй и 30% - третьей. Вероятность обращения в суд для разрешения имущественного спора для каждой социальной группы соответственно равна 0,5, 0,4 и 0,1. Случайным образом взятое исковое заявление содержит просьбу разрешить имущественный спор. Какова вероятность того, что этот иск принадлежит представителю третьей группы?
54. Случайная величина X задана функцией распределения
Какова вероятность того, что в результате испытания величина Х примет значение, заключённое в интервале (0, 1/3)?
55. Количество Х принимаемых за час звонков по домашнему телефону имеет распределение Пуассона. Среднее количество принимаемых за час звонков - l = 2. Чему равна вероятность того, что в течение часа будет принято более 1 звонка?
56. Случайная величина задана рядом распределения
| xi | –1 | 0 | 1 | 2 | 3 |
| pi | 0,2 | 0,2 | 0,1 | 0,3 | 0,2 |
Найти математическое ожидание данной случайной величины.
57. Случайная величина задана рядом распределения
| xi | –1 | 0 | 3 | 4 | 6 |
| pi | 0,2 | 0,2 | 0,3 | 0,1 | 0,2 |
Найти дисперсию данной случайной величины.
58. Известны: математические ожидания случайных величин Х и Y: МХ = 5, М Y = 3, а также зависимость случайной величины Z = 3Х – 2Y. Чему равно математическое ожидание случайной величины Z?
59. Результаты изучения работы федеральных судей за отчётный период представлены в таблице:
| Количество рассмотренных исков | (10; 20) | (20; 30) | (30; 40) |
| Количество судей | 5 | 3 | 2 |
Найти выборочные среднее и дисперсию числа рассмотренных исков.
Приложение 1
Образец титульного листа
Государственное образовательное учреждение
высшего профессионального образования
Российская академия правосудия
Центральный филиал
Кафедра правовой информатики, информационного права
и естественнонаучных дисциплин
Контрольная работа
по курсу
« Элементы теории вероятностей и математической статистики в юридической деятельности»
Вариант № ___
Подготовил:
студент
(подпись, инициалы, фамилия)
учебная группа
дата
Проверил:
преподаватель
(подпись, инициалы, фамилия)
результат проверки
дата
замечания:
ВОРОНЕЖ
201_
Приложение 2
Образец титульного листа
Государственное образовательное учреждение
высшего профессионального образования
Российская академия правосудия
Центральный филиал
Кафедра правовой информатики, информационного права
и естественнонаучных дисциплин
Контрольное задание
по курсу
« Элементы теории вероятностей и математической статистики в юридической деятельности»
Вариант № ___
Подготовил:
студент
(подпись, инициалы, фамилия)
учебная группа
дата
Проверил:
преподаватель
(подпись, инициалы, фамилия)
результат проверки
дата
замечания:
ВОРОНЕЖ
201_
Приложение 3
Таблицы случайных чисел, используемых в задачах для самостоятельного решения
Таблица П. 3.1
Последовательность случайных чисел для контрольной работы
| 10 | 09 | 73 | 25 | 33 | 76 | 52 | 01 | 35 | 86 | 34 | 67 | 35 | 48 | 76 | 80 | 95 | 90 | 91 | 17 |
| 85 | 26 | 97 | 76 | 02 | 02 | 05 | 16 | 56 | 92 | 68 | 66 | 57 | 48 | 18 | 73 | 05 | 38 | 52 | 47 |
| 37 | 54 | 20 | 48 | 05 | 64 | 89 | 47 | 42 | 96 | 24 | 80 | 52 | 40 | 37 | 20 | 63 | 61 | 04 | 02 |
| 08 | 42 | 26 | 89 | 53 | 19 | 64 | 50 | 93 | 03 | 23 | 20 | 90 | 25 | 60 | 15 | 95 | 33 | 47 | 64 |
| 99 | 01 | 90 | 25 | 29 | 09 | 37 | 67 | 07 | 15 | 38 | 31 | 13 | 11 | 65 | 88 | 67 | 67 | 43 | 97 |
| 12 | 80 | 79 | 99 | 70 | 80 | 15 | 73 | 61 | 47 | 64 | 03 | 23 | 66 | 53 | 98 | 95 | 11 | 68 | 77 |
| 66 | 06 | 57 | 47 | 17 | 34 | 07 | 27 | 68 | 50 | 36 | 69 | 73 | 61 | 70 | 65 | 81 | 33 | 98 | 85 |
| 31 | 06 | 01 | 08 | 05 | 45 | 57 | 18 | 24 | 06 | 35 | 30 | 34 | 26 | 14 | 86 | 79 | 90 | 74 | 39 |
Таблица П. 3.2
Последовательность случайных чисел для контрольного задания
| 0,414 | 0,011 | 0,666 | -1,132 | -0,410 | -1,077 | 1,484 | -0,340 | 0,789 | -0,494 |
| 0,364 | -1,237 | -0,044 | -0,111 | -0,210 | 0,931 | 0,616 | -0,377 | -0,433 | 1,048 |
| -0,037 | 0,759 | 0,609 | -2,043 | -2,290 | 0,404 | -0,543 | 0,486 | 0,869 | 0,347 |
| 2,816 | -0,464 | -0,632 | -1,614 | 0,372 | -0,074 | -0,916 | 1,314 | -0,038 | 0,673 |
| 0,563 | -0,107 | 0,131 | -1,808 | 0,284 | 0,458 | 1,307 | -1,625 | -0,629 | -0,504 |
| -0,006 | -0,131 | 0,048 | 1,879 | -1,016 | 0,360 | -0,119 | 2,331 | 1,672 | -1,053 |
| 0,840 | 0,246 | -0,237 | -1,312 | 1,603 | -0,952 | -0,566 | 1,600 | 0,465 | 1,951 |
| 0,110 | 0,251 | 0,116 | -0,957 | -0,190 | 1,479 | -0,986 | 1,249 | 1,934 | 0,070 |
| -1,358 | -1,246 | -0,959 | -1,297 | -0,722 | 0,925 | 0,783 | -0,402 | 0,619 | 1,826 |
| 1,272 | -0,945 | 0,494 | 0,050 | -1,696 | 1,876 | 0,063 | 0,132 | 0,682 | 0,544 |
| -0,417 | -0,666 | -0,104 | -0,253 | -2,543 | -1,133 | 1,987 | 0,668 | 0,360 | 1,927 |
| 1,183 | 1,211 | 1,765 | 0,035 | -0,359 | 0,193 | -1,023 | -0,222 | -0,616 | -0,060 |
| -1,319 | -0,785 | -0,430 | -0,298 | 0,248 | -0,088 | -1,379 | 0,295 | -0,115 | -0,621 |
| -0,618 | 0,209 | 0,979 | 0,906 | -0,096 | -1,376 | 1,047 | -0,872 | -2,200 | -1,384 |
Приложение 4
Таблица значений функции Лапласа 
| х | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0,0000 | 0040 | 0080 | 0120 | 0160 | 0199 | 0239 | 0279 | 0319 | 0359 | |
| 0,1 | 0398 | 0438 | 0478 | 0517 | 0557 | 0596 | 0636 | 0675 | 0714 | 0753 | |
| 0,2 | 0793 | 0832 | 0871 | 0910 | 0948 | 0987 | 1026 | 1064 | 1103 | 1141 | |
| 0,3 | 1179 | 1217 | 1255 | 1293 | 1331 | 1368 | 1406 | 1443 | 1480 | 1517 | |
| 0,4 | 1554 | 1591 | 1628 | 1664 | 1700 | 1736 | 1772 | 1808 | 1844 | 1879 | |
| 0,5 | 1915 | 1950 | 1985 | 2019 | 2054 | 2088 | 2123 | 2157 | 2190 | 2224 | |
| 0,6 | 2257 | 2291 | 2324 | 2357 | 2389 | 2422 | 2454 | 2486 | 2517 | 2549 | |
| 0,7 | 2580 | 2611 | 2642 | 2673 | 2708 | 2734 | 2764 | 2794 | 2823 | 2852 | |
| 0,8 | 2881 | 2910 | 2939 | 2967 | 2995 | 3023 | 3051 | 3078 | 3106 | 3133 | |
| 0,9 | 3159 | 3186 | 3212 | 3238 | 3264 | 3289 | 3315 | 3340 | 3365 | 3389 | |
| 1,0 | 3413 | 3438 | 3461 | 3485 | 3508 | 3531 | 3554 | 3577 | 3599 | 3621 | |
| 1,1 | 3643 | 3665 | 3696 | 3708 | 3729 | 3749 | 3770 | 3790 | 3810 | 3830 | |
| 1,2 | 3849 | 3869 | 3883 | 3907 | 3925 | 3944 | 3962 | 3980 | 3997 | 4015 | |
| 1,3 | 4032 | 4049 | 4066 | 4082 | 4099 | 4115 | 4131 | 4147 | 4162 | 4177 | |
| 1,4 | 4192 | 4207 | 4222 | 4236 | 4251 | 4265 | 4279 | 4292 | 4306 | 4319 | |
| 1,5 | 4332 | 4345 | 4357 | 4370 | 4382 | 4394 | 4406 | 4418 | 4429 | 4441 | |
| 1,6 | 4452 | 4463 | 4474 | 4484 | 4495 | 4505 | 4515 | 4525 | 4535 | 4545 | |
| 1,7 | 4554 | 4564 | 4573 | 4582 | 4591 | 4599 | 4608 | 4616 | 4625 | 4633 | |
| 1,8 | 4641 | 4649 | 4656 | 4664 | 4671 | 4678 | 4686 | 4693 | 4699 | 4706 | |
| 1,9 | 4713 | 4719 | 4726 | 4732 | 4738 | 4744 | 4750 | 4756 | 4761 | 4767 | |
| 2,0 | 4772 | 4778 | 4783 | 4788 | 4793 | 4798 | 4803 | 4808 | 4812 | 4817 | |
| 2,1 | 4821 | 4826 | 4830 | 4834 | 4838 | 4842 | 4846 | 4850 | 4854 | 4857 | |
| 2,2 | 4861 | 4864 | 4868 | 4871 | 4875 | 4878 | 4881 | 4884 | 4887 | 4890 | |
| 2,3 | 4893 | 4896 | 4898 | 4901 | 4904 | 4906 | 4909 | 4911 | 4913 | 4916 | |
| 2,4 | 4918 | 4920 | 4922 | 4925 | 4927 | 4929 | 4931 | 4932 | 4034 | 4936 | |
| 2,5 | 4938 | 4940 | 4941 | 4943 | 4945 | 4946 | 4948 | 4949 | 4951 | 4951 | |
| 2,6 | 4953 | 4955 | 4956 | 4957 | 4959 | 4960 | 4961 | 4962 | 4963 | 4964 | |
| 2,7 | 4965 | 4966 | 4967 | 4968 | 4969 | 4970 | 4971 | 4972 | 4973 | 4974 | |
| 2,8 | 4974 | 4975 | 4976 | 4977 | 4977 | 4978 | 4979 | 4979 | 4980 | 4981 | |
| 2,9 | 4981 | 4982 | 4982 | 4983 | 4984 | 4984 | 4985 | 4985 | 4986 | 4986 | |
| х | х | х | х | ||||||||
| 3,0 | 0,49865 | 3,5 | 0,49977 | 4,0 | 0,499968 | 4,5 | 0,4999966 | ||||
| 3,1 | 0,49903 | 3,6 | 0,49984 | 4,1 | 0,499979 | 4,6 | 0,4999979 | ||||
| 3,2 | 0,49931 | 3,7 | 0,49989 | 4,2 | 0,499987 | 4,7 | 0,4999987 | ||||
| 3,3 | 0,49952 | 3,8 | 0,49993 | 4,3 | 0,499991 | 4,8 | 0,4999992 | ||||
| 3,4 | 0,49966 | 3,9 | 0,49995 | 4,4 | 0,499995 | 4,9 | 0,4999995 | ||||
Приложение 5
Таблица значений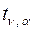 
распределения Стьюдента
( 
– число степеней свободы)
| a n | Уровень доверия a | |||
| 0,90 | 0,95 | 0,98 | 0,99 | |
| 1 | 6,31 | 12,7 | 31,82 | 63,7 |
| 2 | 2,92 | 4,30 | 6,97 | 9,92 |
| 3 | 2,35 | 3,18 | 4,54 | 5,84 |
| 4 | 2,13 | 2,78 | 3,75 | 4,6 |
| 5 | 2,01 | 2,57 | 3,37 | 4,03 |
| 6 | 1,94 | 2,45 | 3,14 | 3,71 |
| 7 | 1,89 | 2,36 | 3,00 | 3,5 |
| 8 | 1,86 | 2,31 | 2,9 | 3,36 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 |
| 11 | 1,80 | 2,22 | 2,72 | 3,11 |
| 12 | 1,78 | 2,18 | 2,68 | 3,05 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 |
| 14 | 1,76 | 2,14 | 2,62 | 2,98 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 |
| 16 | 1,75 | 2,12 | 2,58 | 2,92 |
| 17 | 1,74 | 2,11 | 2,57 | 2.90 |
| 18 | 1,73 | 2,10 | 2,55 | 2,88 |
| 19 | 1,73 | 2,09 | 2,54 | 2,86 |
| 20 | 1,73 | 2,09 | 2,53 | 2,85 |
| 30 | 1,70 | 2,04 | 2,46 | 2,75 |
| 40 | 1,68 | 2,02 | 2,42 | 2,70 |
| 60 | 1,67 | 2,00 | 2,39 | 2,66 |
| 120 | 1,66 | 1,98 | 2,36 | 2,62 |
| ¥ | 1,64 | 1,96 | 2,33 | 2,58 |
Приложение 6
Критические точки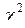 
-распределения
(n – число степеней свободы)
| g n | Уровень значимости g | |||
| 0,01 | 0,05 | 0,1 | 0,2 | |
| 1 | 0,00016 | 0,00393 | 0,0158 | 0,0642 |
| 2 | 0,0201 | 0,103 | 0,211 | 0,446 |
| 3 | 0,115 | 0,352 | 0,584 | 1,005 |
| 4 | 0,297 | 0,711 | 1,064 | 1,649 |
| 5 | 0,554 | 1,145 | 1,610 | 2,343 |
| 6 | 0,872 | 1,635 | 2,204 | 3,070 |
| 7 | 1,239 | 2,167 | 2,833 | 3,822 |
| 8 | 1,646 | 2,733 | 3,490 | 4,594 |
| 9 | 2,088 | 3,325 | 4,168 | 5,380 |
| 10 | 2,558 | 3,940 | 4,865 | 6,179 |
| 11 | 3,053 | 4,575 | 5,578 | 6,989 |
| 12 | 3,571 | 5,226 | 6,304 | 7,807 |
| 13 | 4,107 | 5,892 | 7,042 | 8,634 |
| 14 | 4,660 | 6,571 | 7,790 | 9,467 |
| 15 | 5,229 | 7,262 | 8,547 | 10,30 |
| 16 | 5,812 | 7,962 | 9,312 | 11,152 |
| 17 | 6,408 | 8,672 | 10,085 | 12,002 |
| 18 | 7,015 | 9,390 | 10,865 | 12,857 |
| 19 | 7,633 | 10,117 | 11,651 | 13,716 |
| 20 | 8,260 | 10,851 | 12,443 | 14,578 |
| 21 | 8,897 | 11,591 | 13,240 | 15,445 |
| 22 | 9,542 | 12,338 | 14,041 | 16,314 |
| 23 | 10,196 | 13,091 | 14,848 | 17,187 |
| 24 | 10,856 | 13,848 | 15,659 | 18,062 |
| 25 | 11,524 | 14,611 | 16,473 | 18,94 |
| 26 | 12,198 | 15,379 | 17,292 | 19,820 |
| 27 | 12,879 | 16,151 | 18,114 | 20,703 |
| 28 | 13,565 | 16,928 | 18,939 | 21,588 |
| 29 | 14,256 | 17,708 | 19,768 | 22,475 |
| 30 | 14,953 | 18,493 | 20,599 | 23,364 |
| 35 | 18,5 | 22,5 | 24,8 | 27,8 |
| 40 | 22,2 | 26,5 | 29,1 | 32,3 |
| 45 | 25,9 | 30,6 | 33,4 | 36,9 |
| 50 | 29,7 | 34,8 | 37,7 | 41,4 |
| 75 | 49,5 | 56,1 | 59,8 | 64,5 |
| 100 | 70,1 | 77,9 | 82,4 | 87,9 |
Учебное издание
Александр Владимирович Мишин
элементы теории вероятностей
Последнее изменение этой страницы: 2019-04-10; Просмотров: 223; Нарушение авторского права страницы
распределения Стьюдента . . . .