Анализ расчета цепей постоянного тока с одним источником ЭДС (вопрос 14)

Переходные процессы в цеп и с последовательным соединением резистивного, индуктивного и емкостного элементов (вопрос 60)

Рассмотрим апериодическую разрядку конденсатора (рисунок 5.6). Если ключ  переключить из положения  в положение , то образуется накоротко замкнутый  контур, в котором до коммутации конденсатор заряжен до напряжения источника .

Рисунок 5.6 – Апериодическая разрядка конденсатора

 

После коммутации в замкнутом  контуре протекает свободный процесс, который, согласно второму правилу Кирхгофа, описывается однородным уравнением:

.

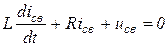Так как 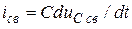, то

.

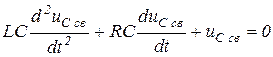Характеристическое уравнение имеет вид:

, или ,

где корнями данного уравнения являются два корня:

.

Если в колебательном контуре резонансная частота  и , то выражение для определения корней характеристического уравнения можно переписать:

.

Характер свободного процесса зависит от вида корней характеристического уравнения, которые, в свою очередь, зависят от соотношения параметров цепи 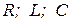. Свободный процесс, наблюдаемый в замкнутом  контуре после коммутации, представляет собой апериодическую разрядку конденсатора. Апериодической называется разрядка конденсатора, заряженного до напряжения , через резистор и индуктивную катушку, когда напряжение на конденсаторе постепенно спадает до нуля. Апериодический процесс разрядки конденсатора имеет место, если корни характеристического уравнения вещественны, т. е. если , или , или  получается пара разных корней.

Сопротивление  называется критическим, так как оно является наименьшим сопротивлением контура, когда еще имеет место апериодический процесс разрядки конденсатора. При  корни характеристического уравнения получаются комплексными и сопряженными. Таким образом, корни характеристического уравнения  и  будут вещественными и различными, если выполняется условие . Если корни различны, то общее решение однородного дифференциального уравнения имеет вид:

,

где  и − постоянные интегрирования, а  и 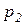 − вещественные и различные корни, которые должны быть отрицательными, так как свободный процесс должен быть затухающим во времени.

Так как при разрядке конденсатора в накоротко замкнутом  контуре процесс является свободным, то переходные значения напряжения  и тока  равны их свободным значениям, т. е.  и . Ток цепи:

.

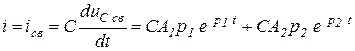Подставляя начальные условия при 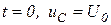 и  в

;

и решая совместно систему уравнений, определяем постоянные интегрирования:                                      

Окончательно получаем, что

.

Напряжение на индуктивном элементе  определяется по формуле;

.

Так как для свободного процесса, имеющего апериодический характер, корни характеристического уравнения должны быть вещественными и различными, то, согласно (36) и (37), они также всегда должны быть отрицательными.

Как видно из формул (42), (43) и (44), корни характеристических уравнений входят в показатели экспонент; следовательно, свободные процессы в цепях всегда затухают и тем быстрее, чем больше абсолютное значение корня характеристического уравнения. Если согласно этим формулам характер изменения переходных процессов представить в виде кривых, то каждая из них будет представлять собой сумму двух экспонент с коэффициентами затухания  и 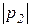 соответственно. Значение коэффициентов затухания находят по формуле (37). Кривые изменения напряжений и их составляющих на емкостном и индуктивном элементах, а также кривые изменения тока и его составляющих приведены на рисунке 10, а) – в).

 

                                                  а)

 

                                                     б)     

 

 

                                            в)

 

Рисунок 10 − Зависимости изменения токов и напряжений и их составляющих на емкостном и индуктивном элементах

Из рисунка видно, что напряжение на емкостном элементе  постепенно уменьшается от начального значения , а ток в начальный отрезок времени, возрастая от нуля, достигает максимума, а затем, как и , также затухает. Когда 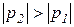, то . Это означает, что в зависимостях , состоящих из алгебраической суммы двух экспонент, первая экспонента затухает медленнее, чем вторая. Вследствие этого напряжение на емкостном элементе  постепенно убывает, оставаясь всегда положительным, так как его первая экспонента положительна и больше второй отрицательной экспоненты. Кривая тока  (рисунок 10, б) находится в отрицательной области, так как происходит апериодическая разрядка конденсатора.

Так как ток , то максимум кривой тока 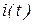 и точка перегиба кривой напряжения  имеют место в один и тот же момент времени  (рисунок 10, а), б), а кривая 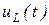 в этот момент времени меняет знак, что следует из соотношения  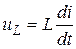(рисунок 10, в). Время  можно найти, приравнивая нулю производную . Напряжение на индуктивном элементе возникает скачком, принимая в начальный момент  значение , затем уменьшается по абсолютному значению, проходит через нуль при равенстве экспонент и, став положительным, возрастает до некоторого максимального значения, после которого, уменьшаясь, стремится к нулю.

Следует отметить, что, согласно (37), увеличение индуктивности 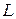 приводит к уменьшению абсолютных значений  и 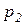 и, как следствие, к замедлению возрастания тока  и спада напряжения на емкостном элементе .

 

 

Раздел 5 Магнитные цепи

Лекция 7

В различных электротехнических устройствах между источником энергии и приемником включают электрические фильтры в виде четырехполюсников или цепных схем, чтобы пропускать к приемнику только токи заданного диапазона частоты. Цепные схемы состоят из каскадно-включенных четырехполюсников, называемых звеньями. При этом выходные схемы каждого предыдущего звена соединяются с входными схемами последующего.

Электрический фильтр − пассивный четырехполюсник, пропускающий некоторую определенную полосу частот с малым затуханием, вне этой полосы частот затухание велико.

Фильтров

Полосой пропускания реактивного фильтра является область частот, при которой собственное затухание реактивного фильтра равно нулю ( ).

Для любого симметричного реактивного фильтра в полосе пропускания, т.е. при :

Анализ расчета цепей постоянного тока с одним источником ЭДС (вопрос 14)

 

С помощью правил Кирхгофа можно рассчитать любую электрическую цепь, в том числе цепь постоянного тока с одним источником энергии. В этом случае необходимо составить систему уравнений по правилам Кирхгофа и решать ее относительно неизвестных токов. Для определения токов и напряжений каждого элемента цепи с одним источником электрической энергии можно использовать метод эквивалентных преобразований («метод свертки»).   

Суть метода рассмотрим на примере цепи, схема которой приведена на рисунке 24, а). Пусть известны значения сопротивлений резисторов , ЭДС  и его внутреннего сопротивления . Требуется определить токи во всех участках цепи и напряжение, которое покажет вольтметр (сопротивление его бесконечно велико), включенный между точками  и .

Для решения такой задачи отдельные участки электрической цепи с последовательно или параллельно соединенными элементами заменяют одним эквивалентным элементом. Схему электрической цепи упрощают постепенным преобразованием ее участков. В этом случае схеме цепи состоит из последовательно соединенного источника электрической энергии и одного эквивалентного пассивного элемента. Так, резисторы  и   соединены последовательно, а резистор   к ним параллельно, поэтому их эквивалентное сопротивление запишется как

, где _.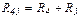

Сопротивления 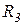 и   соединены последовательно (рисунок 24, б), поэтому их общее сопротивление будет равно .

Сопротивления  и  соединены параллельно, следовательно .

Эквивалентное (входное) сопротивление всей цепи находят из уравнения:

.

               

 

 

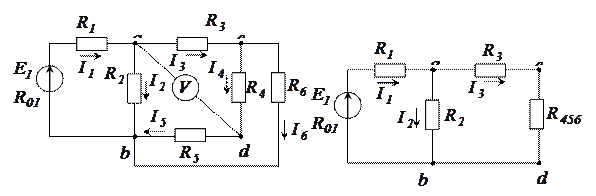
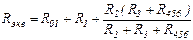                    а)                                                                               б)

 

Рисунок 24

Ток 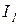  в неразветвленной части схемы определяют из закона Ома:

.

Токи  и  определяют

Токи определяют по следующим формулам:  

; .

Зная ток , можно найти ток  по-другому. На основании второго правила Кирхгофа, определяем напряжение на участке 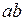       , тогда значение тока будет равно _.

Показания вольтметра можно определить, составив уравнение по второму правилу Кирхгофа, например, для контура : 

.

Правильность вычисленных значений можно проверить, воспользовавшись первым правилом Кирхгофа или уравнением баланса мощностей, которые для схемы, изображенной на рисунке 1.1, имеют вид:   

Если заданы значения сопротивлений ветвей электрической цепи (рисунок 24, а) и ЭДС источника , то для нахождения токов в ветвях можно воспользоваться методом подобия (методом пропорциональных величин). Этот метод применим только для расчета линейных цепей, т. е. цепей с постоянными значениями сопротивлений.

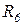Воспользуемся свойствами линейных цепей для определения токов схемы, изображенной на рисунке 24, а) в такой последовательности: зададимся произвольным значением тока  в резисторе , наиболее удаленном от источника питания. Как правило, это значение тока берут равным единице. По заданному току  и сопротивлению  определяем напряжение . Далее определяем параметры цепи от действия тока .

 ; ; ; .

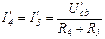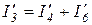После этого находим значение ЭДС   как .

Однако найденное значение ЭДС  в общем случае отличается от заданной величины ЭДС . Поэтому для определения действительных значений токов и напряжений вычисляем так называемый коэффициент подобия 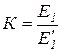. Умножая на него полученные при расчете значения токов и напряжений, находим действительные значения токов и напряжений цепи. Метод пропорциональных величин особенно эффективен при расчете разветвленных линейных электрических цепей с одним источником.

 

123456789Следующая ⇒

Поделиться: