
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Учебно-методический комплекс. Дисциплины (УМКД)Стр 1 из 19Следующая ⇒
Учебно-методический комплекс Дисциплины (УМКД) Основы математической обработки информации 050100.62 Педагогическое образование Москва, 2017 Учебный план. 3 План лекционных занятий. 3 План лабораторных работ. 3 Домашние задания. 3 Домашнее задание №1. 3 Домашнее задание №2. 3 Домашнее задание №3. 3 Технологическая карта. 3 Литература. ….//Зак. Описание лабораторных работ. 3 Лабораторнаяработа№1. Макрокомандыпрограммы Microsoft Word 200. 3 Лабораторнаяработа№2. МакрокомандыпрограммыMicrosoft Excel 200. 3 Лабораторнаяработа№3. Частотныйанализпоэтическихтекстовпоначальнойбукве. 3 Лабораторнаяработа№4. Частотныйанализпоэтическихтекстовповсембуквам.. 3 Лабораторнаяработа№5. Формальныйанализавторской. 3 индивидуальностилитературноготекста. 3 Лабораторная работа №6. Создание презентаций в программе MS Power Point…..……..….13 Лабораторная работа №7. Работа с программой PhotoShop ………………………162
Проект. Компьютерный контент-анализ текстовой информации (ККАТИ) -поэтических текстов конкретного автора (по выбору преподавателя) 3 Пример-образец выполнения студентами проекта ККАТИ
Учебный план План лекционных занятий (теоретические этапы обучения)
План лабораторных работ (практические этапы обучения)
Домашние задания (самостоятельная работа) Домашнее задание- блок №1 Системы счисления Задача 1. Выполнить перевод числа 19 в двоичную систему счисления.
Ответ: 19 = 100112
Задача 2 Выполнить перевод числа 19 в шестнадцатеричную систему счисления.
Ответ: 19 = 1316
Задача 3 Выполнить перевод числа 123 в шестнадцатеричную систему счисления.
Ответ: 123 = 7В16
Задача 4 Выполнить перевод числа 1316 в десятичную систему счисления.
Ответ: 1316 = 19
Задача 5 Выполнить перевод числа 100112 в десятичную систему счисления.
Ответ: 100112 = 19
Задача 6 Выполнить перевод числа 100112 в шестнадцатеричную систему счисления.
Ответ: 100112 = 1316
Задача 7 Выполнить перевод числа 1316 в двоичную систему счисления.
Ответ: 1316 = 100112
Задача 8 Выполнить перевод числа 0,847 в двоичную систему счисления.
Ответ: 0,847 = 0,11012
Задача 9 Выполнить перевод числа 0,847 в шестнадцатеричную систему счисления.
Ответ: 0,847 = 0,D8D16
Задача 10 Выполнить перевод из двоичной системы счисления в десятичную систему числа 0,11012
Ответ: 0,11012 = 0,8125
Задача 11 Выполнить перевод из шестнадцатеричной системы счисления в десятичную числа 0,D8D16.
Ответ: 0,D8D16 = 0,84692
Задача 12 Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,11012.
Ответ: 0,11012 = 0,D16
Задача 13 Выполнить перевод из шестнадцатеричной системы счисления в двоичную числа 0,2А16.
Ответ: 0,2А16 = 0,00101012
Задача 14 Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847.
Ответ: 19,847 = 13,D8D16.
Домашнее задание - блок №2
Задача 1. Пусть высказывание А есть: «Множество А есть совокупность некоторых объектов», высказывание В есть: «Множество А есть подмножество множества В». Тогда какое высказывание будет дизъюнкцией этих высказываний? Ответ: «Множество А есть совокупность некоторых объектов, или множество А есть подмножество множества В».
Задача 2. Пусть есть высказывание А есть: «Множество А есть подмножество множества В », высказывание В есть: «Все элементы множества А являются элементами множества В». Тогда результатом какай операции над высказываниями А и В будет высказывание «Множество А есть подмножество множества В тогда и только тогда, когда все элементы множества А являются элементами множества В» ? Ответ: Результатом эквиваленции высказываний А и В.
Задача 3. Заполнить таблицу истинности для сложного высказывания
Ответ:
Задача 4. Заполнить таблицу истинности для сложного высказывания
Ответ:
.
Задача 5. Заполнить таблицу истинности для сложного высказывания
Ответ:
Задача 6. Заполнить таблицу истинности для сложного высказывания
Ответ:
Задача 7. Какой таблично-заданной функции соответствует формула
Ответ:
Задача 8. Какой таблично-заданной функции соответствует формула
Ответ:
. Задача 9. Написать ДНФ, соответствующую таблично заданной функции
Ответ:
Задача 10. Написать ДНФ, соответствующую таблично заданной функции
Ответ:
Задача 11. Написать КНФ, соответствующую таблично заданной функции
Ответ:
Задача 12. Написать КНФ, соответствующую таблично заданной функции
Ответ:
Домашнее задание – блок №3
Задание 1. В фон-неймановской архитектуре компьютера часть процессора, которая выполняет команды, называется…
Варианты ответов: 1. устройством ввода 2. устройством управления (УУ) 3. памятью 4. арифметико-логическим устройством (АЛУ)
Решение: Большинствосовременныхкомпьютеровоснованонаобщихлогическихпринципах, сформулированных Джоном фон Нейманом. Основные устройства такого компьютера: Ответ: арифметико-логическим устройством (АЛУ)
Задание 2 : На материнской плате персонального компьютера размещаются … Варианты ответов: 1. системные шины 2. контроллер винчестера 3. контроллер клавиатуры 4. винчестер Решение: На материнской (системной) плате персонального компьютера обычно размещаются: центральный процессор, контроллеры некоторых устройств (например, клавиатуры, долговременных запоминающих устройств, портов), системные шины с разъемами для подключения дополнительных устройств, разъемы для модулей оперативной памяти, кэш-память, память с программой базовой системы ввода/вывода (BIOS) . Ответ: системные шины, контроллер винчестера, контроллер клавиатуры Задание 3 : Оперативное запоминающее устройство (ОЗУ) относится к виду памяти… Задание 4 : При вводе символов с клавиатуры для переключения между режимами вставки и замены служит клавиша … Задание 5 : Верными являются утверждения, что …оперативная память не обладает системой команд, манипулятор «Мышь» обладает системой команд, контроллеры устройств компьютера обладают системой команд, системой команд обладает процессор
Задание 6 : К внутренней памяти относятся …
Задание 7 : ХарактеристикойLCDмониторов персонального компьютера является …
Задание 8 : К устройствам только вывода информации относятся…. плоттер, дисплей, стриммер, принтер, аудиоколонки; мышь, манипулятор, сканер, принтер, аудиоколонки; дисплей, сканер, принтер, аудиоколонки; дисплей, принтер, плоттер, аудиоколонки
Задание 9 : Системной шиной компьютера не является… шина Адреса, шина управления, шина данных, виртуальная шина
Задание 10 : Логическая организация и структура аппаратных и программных ресурсов вычислительной системы составляет … Задание 1. Прикладной программой является … Варианты ответов: 1. антивирус Касперского 2. Borland Delphi 3. драйвер управления монитором 4. Adobe Photoshop
Решение: Прикладное программное обеспечение – это программы, с помощью которых выполняются конкретные задачи. Спектр этих задач необычайно широк – от производственных до творческих и развлекательно-обучающих: редактирование текстовых документов, создание рисунков или картинок, создание электронных таблиц, баз данных, верстка полиграфических изданий, обработка видеоматериалов. Ответ: Adobe Photoshop Задание 2. Совокупность средств операционной системы, обеспечивающих взаимодействие устройств и программ врамках вычислительной системы, – это… Варианты ответов: 1. драйвер 2. графический интерфейс 3. аппаратно-программный интерфейс 4. пользовательский интерфейс Решение: Термин «интерфейс» широко используется в областях, где человеку приходится иметь дело с обработкой информации на компьютере. В переводе с английского языка Interface означает внешнее лицо. В компьютерном мире известно множество разновидностей интерфейсов: интерфейс пользователя, графический интерфейс, интерфейс ввода-вывода, внешний или внутренний интерфейс, интеллектуальный интерфейс, человеко-машинный интерфейс, программный интерфейс и др. Ответ: аппаратно-программный интерфейс Задание 3. Дана маска для имени файла: k*t.d*. Не удовлетворяет указанному шаблону имя файла…kot.d, kotenok.doc, kit_kat.dll, kompot.docx
Задание 4. Выполнение представленной на рисунке операции в Microsoft OfficeWord приводит к изменению …
Задание 5. Указатель мыши в MS Excel имеет вид
Задание 6. Дан фрагмент электронной таблицы. После выполнения сортировки по возрастанию сначала по столбцу Страна, затем по столбцу Программист строки расположатся в порядке …
Задание 7. Утверждение «Цвет и форма не отделимы друг от друга, но цвет первичен, а форма не существует без цвета» относится к графике…
Задание 8. Заливка с плавным переходом от одного цвета к другому или между разными оттенками одного цвета называется …
Задание 9. Структура таблицы реляционной базы данных полностью определяется…
Задание 10. Основными объектами реляционной базы данных являются …
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра информатизации образования ИНСТИТУТА МАТЕМАТИКИ, ИНФОРМАТИКИ И ЕСТЕСТВЕННЫХ НАУК ГАОУ ВО МГПУ Технологическая карта
Базовый блок (проверка сформированности компетенций) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тема или задание текущей аттестационной работы | Тип контроля/дата | Аудиторная или внеаудиторная нагрузка | Набран-ные баллы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. Посещение лекционных занятий | Текущий контроль | Аудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Работа над конспектом курса (записи лекций, теоретических и прикладных материалов зад.ППС) | Вконце семестра | Аудиторная и внеаудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. Выполнение лабораторных работ №1-2. | Проверка работы | Аудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. Выполнение лабораторных работ №3-4 | Проверка работы/ межсессионная аттестация | Аудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. Выполнение лабораторных работ №5-7 | Проверка работы | Аудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. Выполнение проекта | Проверка работы | Аудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. Защита проекта | Проверка работы | Аудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. Выполнение домашнего задания №1 | Проверка работы | Внеаудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. Выполнение домашнего задания №2 | Проверка работы/ межсессионная аттестация | Внеаудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. Выполнение домашнего задания №3 | Проверка работы | Внеаудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. Зачет | В конце семестра | Аудиторная |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Итого: |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание:
· Каждое задание (1-10 пункты тех. карты) оценивается максимум в восемь баллов.
· Баллы по первым двум позициям выставляются лектором на зачете (экзамене).
· За работы, указанные в технологической карте, сданные не в срок, балл снижается.
· Студент, может увеличить количество баллов, набранных в течение семестра на зачете или экзамене.
· Студенты, набравшие 51 балл и более - получают зачет автоматом. Студент, пожелавший увеличить баллы - сдает непосредственно зачет.
· Результаты зачета не снижают набранных баллов за семестр, а увеличивают баллы.
Преподаватели: лекторы – проф. Полтавский А.В.,
преподаватель – Гриншкун В.В.
Утверждено на заседании КИО ИМИЕН ГАОУ ВО МГПУ
« » 2017г.
Протокол №1
Заведующий кафедрой
профессор, д.п.н. В.В. Гриншкун
ЛИТЕРАТУРА
К изучению курса « Основы математической обработки информации»
1. Полтавский А.В. Программные средства вычислительных систем. Часть I. ЭВМ первых поколений. Учебное пособие.– М.: МГПУ, 2015 – 87 с.
2. Заславская О.Ю., Левченко И.В. Теоретический материал для подготовки к вступительным испытаниям по информатике и ИКТ. М.: МГПУ, 2005 – 66 с.
3. Полтавский А.В. Программные средства вычислительных систем. Часть II. ЭВМ третьего и четвертого поколений. Учебное пособие.– М.: МГПУ, 2016 – 96 с.
4. Полтавский А.В. Основы математической обработки информации вычислительных систем. . Учебное пособие.– М.: МГПУ, 2017 – 104 с.
5. Новиков А.М., Новиков Д.А. Методология [сайт]. URL: http: // metodologya.
6. Бубнов В.А., Яковлева О.В. Математика и информатика. Программа, методические указания и компьютерный практикум. – М.: МГПУ, 2007.
7. Гришин М.П. Математика и информатика. – М.: МГПУ, 2005.
8. Национальный открытый университет «ИНТУИТ» [электр. ресурс]. URL: www.intuit.ru / Курс «Введение в математику».
9. К. Поляков «Преподавание, наука и жизнь». Сайт. [электр. ресурс]. URL: Krolyakov.narod.ru / school / flash.html.
Технология выполнения:
Выделите второй и третий столбцы таблицы и нажмите ПКМ. В открывшемся ниспадающем меню навести курсор мыши на строку «Выровнять ширину столбцов» и нажать ЛКМ (рис. 50).

Рис. 50. Команда «Выровнять ширину столбца»
В результате ширина каждого из выделенных столбцов принимает значение среднего арифметического изначальной ширины этих столбцов (рис. 51).

Рис. 51. Результат выполнения
23. Макрокоманда «Создание дополнительного документа»
Параметры: - программа: Microsoft Word.
Результат: Рис. 52.
Технология выполнения:
Если при работе с одним документом вам требуется создать новый, то наведите курсор мыши на изображение вкладку «Файл» на панели инструментов окна Word, и нажмите ПКМ. Откроется диалоговое окно с доступными шаблонами. Нажмите ЛКМ на команду «Создать», а затем на шаблон «Новый документ» (рис. 52). Откроется новый текстовый документ.
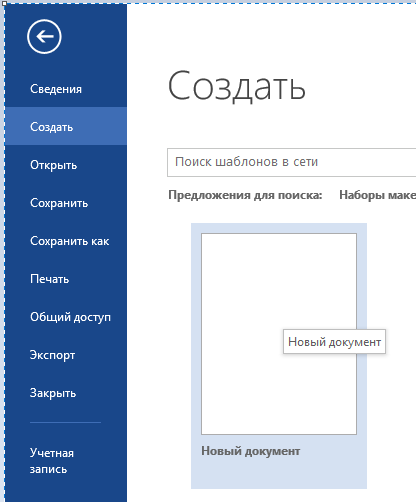
Рис. 52. Создание нового документа
25.
Параметры: - позиция: начало нового документа; - формула:
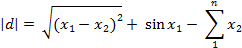
Результат: Рис. 60.
Технология выполнения:
Наведите курсор мыши на вкладку главного меню «Вставка» и нажмите ЛКМ. Появится лента инструментов, среди которых выберите инструмент «Уравнение» (рис. 53). Нажмите ЛКМ.

Рис. 53. Инструмент «Уравнение»
Откроется вкладка «Конструктор» и в документе появится рамка, указывающая место набора формулы (рис. 54).
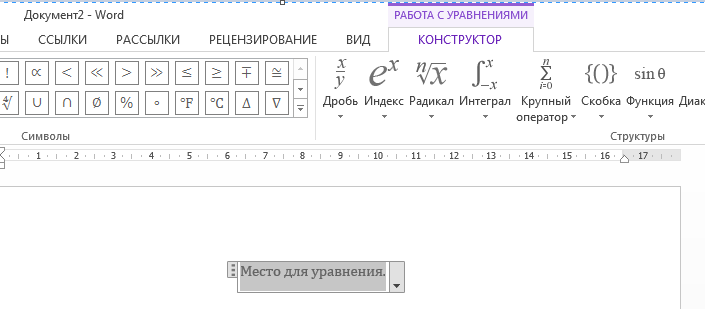
Рис. 54. Вкладка «Конструктор» и рамка для ввода формулы
Перейдите на английскую раскладку и подбирая соответствующие структуры наберите требуемую формулу. Например, для набора знака модуля используется структура «Скобка» (рис. 55). Выбирите требуемую скобку – знак модуля (рис. 55).
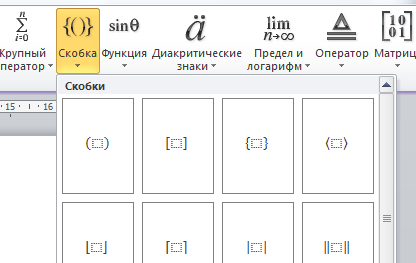
Рис. 55. Структура «Скобки»
Выбирете из всех предлагаемых скобок знак модуля  . Нажмите ЛКМ (рис. 56).
. Нажмите ЛКМ (рис. 56).

Рис. 56. Результат выбора скобки – знак модуля
Активировав квадрат, ограниченный пунктирной линией, в рамке ввода формулы введите с клавиатуры букву «d». Переставив курсор за знак модуля введите с клавиатуры знак «равно». Затем с помощью структуры «Радикал» произведите выбор требуемого знака «Квадратный корень» (рис. 57). Нажмите ЛКМ (рис. 58).

Рис. 57. Структура «Радикал»
Активировав квадрат, под знаком радикала (корня), ограниченный пунктирной линией, в структуре «Индекс» выберите шаблон «Верхний индекс» (рис. 58). Нажмите ЛКМ (рис. 59).

Рис. 58. Структура «Верхний индекс»

Рис. 59. Результат выбора структуры «Верхний индекс»
Активировав квадрат основания шаблона степени, стоящей под знаком корня, введите с клавиатуры скобку и следующую требуемую структуру «Нижний индекс» для ввода с клавиатуры записи «  ».
».
Пользуясь необходимыми структурами и клавиатурой введите все необходимые записи для создания требуемой формулы (рис. 60).
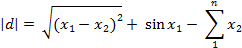
Рис. 60. Набранная формула
Технология выполнения
С помощью кнопки клавиатуры Enter перейдите на следующую страницу документа, в котором Вы набирали формулу.
Выберите вкладку «Разметка страницы» и нажмите ЛКМ. В открывшейся ленте программ выбираем команду «Выровнять» и нажимаем ЛКМ (рис. 61).

Рис. 61. Команда «Выровнять»
В открывшемся каскадном меню выберите «Параметры сетки» (рис. 62). Нажмите ЛКМ.

Рис. 62. «Параметры сетки»
Откроется диалоговое окно «Сетка и направляющие» (рис. 63). В группе параметров «Шаг сетки» в полях «По горизонтали» и «По вертикали» с помощью счетчика поля устанавливается шаг сетки, указанный в параметрах макрокоманды, в данном случае 0,1 см.

Рис. 63. Окно «Сетка и напрвляющие»
Далее следует поставить галочку (если она отсутствует) во флажке «Отображать линии сетки на экране», для чего навести курсор мыши на квадратик левее названия флажка и нажать ЛКМ. Флажок «по вертикали» тоже должен быть установлен. В поле «По вертикали» с помощью счетчика поля устанавливается размер клеточки сетки на экране, измеренный в шагах сетки. В нашем случае, это 5, т.е. высота клетки будет 0,5 см. То же число 5 следует установить в поле «По горизонтали».
Далее следует нажать кнопку «ОК» диалогового окна «Привязка сетки». Рабочее поле документа покроется сеткой (рис. 64).

Рис. 64. Сетка покрывшая поле документа
Технология выполнения
Нажмите на кнопку с изображением прямоугольника с буквой «А» на панели «Иллюстрации» вкладки «Вставка» инструмента «Фигуры»  . Подведите курсор мыши к точке пересечения координатных осей построенных в предыдущей макрокоманде. Нажмите ЛКМ и, не отпуская протяните курсор до образования небольшого прямоугольника (квадрата), отпустите ЛКМ. Появится рамка (рис. 69).
. Подведите курсор мыши к точке пересечения координатных осей построенных в предыдущей макрокоманде. Нажмите ЛКМ и, не отпуская протяните курсор до образования небольшого прямоугольника (квадрата), отпустите ЛКМ. Появится рамка (рис. 69).


Рис. 69. Рамка для надписи Рис. 70. Внесенная надпись
Внутри рамки находится текстовый курсор. Следует выполнить макрокоманду «Установка размера шрифта. Параметры: - размер шрифта: 14 пт.». Затем напечатать текст надписи, в данном случае, цифру «0» (рис. 70). Затем следует убрать заливку и рамку надписи. Для этого наведите курсор мыши на рамку вокруг надписи и нажмите ПКМ, появятся окна «Стиль», «Заливка», «Контур». Выберите команды «Нет заливки» и «Нет контура» в соответствующих окнах. Затем установить курсор мыши за пределами надписи (рис. 71).


Рис. 71. Инструменты «Заливка» и «Контур»
В результате получена декартовая система координат с указанным в ней началом координат и единичным отрезком в две клетки (рис. 72).

Рис. 72. Результат выполнения
Технология выполнения:
Активизируйте прямую линию в системе координат, для этого наведите на нее курсор и нажмите ЛКМ. Линия станет активной, о чем будут свидетельствовать небольшие круги на ее концах (рис. 83).

Рис. 83. Выделение объекта
Нажмите ПКМ и выберите инструмент «Формат фигуры» (рис. 84), нажмите ЛВК. В открывшемся окне (рис. 85) в строке «Ширина» задайте соответствующий размер, в нашем случае 2,25 см. Нажмите ЛКМ.

Рис. 84. Инструмент «Формат фигуры»

Рис.85. Выбор ширины объекта
По начальной букве
Стремительно ворвавшись в школьный курс и продолжая все глубже проникать в предметные области, информационные технологии позволяют не только по-новому взглянуть на процесс обучения, но порой дают возможность анализировать предмет, в данном случае поэзию, с новых позиций.
Рассмотрим применение информационного анализа поэтических текстов на примере произведений поэта Н.М.Рубцова.
Произведение Звезда полей поэта Николая Рубцова (1936-1971) впервые в школьной программе встречается в учебнике по литературе для 6-го класса общеобразовательных учреждений при изучении темы Родная природа в стихотворениях поэтов XX века. Здесь же для раскрытия этой темы приводятся соответствующие тексты стихотворений А. Блока (1880-1921), С. Есенина (1895-1925) и А. Ахматовой (1889-1966) [1].
Для того чтобы научить школьников шестого класса из стихотворных текстов выделять стихи о природе, в [1] предлагается найти и прочитать другие поэтические произведения о природе поэтов - классиков и современных поэтов.
В учебнике - хрестоматии для 7-го класса [2] при раскрытии темы Тихая моя родина, наряду с произведениями В. Брюсова (1873-1924), Ф. Сологуба (1863-1927), С. Есенина и Заболоцкого (1903-1958), Николай Рубцов представлен двумя стихотворениями - Тихая моя родина, Левитан (по мотивам картины «Вечерний звон»). Анализ стихотворений уже усложняется и ученикам предлагается указать литературные приемы, с помощью которых указанные авторы передают свое настроение через стихотворения о природе.
Наконец, в хрестоматии для 11-го класса тематика стихотворений Н. Рубцова расширяется, и школьники могут ознакомиться со следующими произведениями - «В минуту музыки», «Березы», «По дороге к морю», «Звезда полей», «Под ветвями больничных берез» [3].
В старших классах на уроках литературы учеников учат производить анализ произведений как исследовательское прочтение поэтического текста.
Однако изучение творчества того или иного поэта начинается ознакомлением с его биографией, так как «личное» всегда в той или иной мере отражается в произведениях автора.
Действительно, Николай Михайлович Рубцов родился в селе Емецк Архангельской области, расположенном на берегу Северной Двины. В раннем возрасте Н. Рубцов оказался в детском доме села Никольское Тотемского района Вологодской области.
В Никольском он окончил семилетнюю школу, а затем поступил в Тотемский лесотехникум. Получив в 1952 г. паспорт, Н. Рубцов уезжает в Архангельск, из которого в сентябре 1953 г. переезжает в г. Кировск Мурманской области, где учится некоторое время в горном техникуме. В начале 1955 г. он приезжает в Ленинград и работает на одном из заводов рабочим. В этом же году он призывается на военную службу на Северный флот.
Стихи Н. Рубцов писал еще в детском доме, но в Североморске во время службы на эскадренном миноносце он вошел в среду многих пишущих матросов и офицеров. Здесь он начал печататься во флотской газете «На страже Заполярья» и в альманахе «Полярное сияние».
Впервые годы после завершения флотской службы Н. Рубцов возвратился в Ленинград, работал кочегаром, потом шахтовщиком и учился в школе рабочей молодежи. В то время он начал посещать литературное объединение при заводской газете «Кировец», а позднее познакомился со многими молодыми поэтами Ленинграда. Печатался в «Кировце», в сборнике литераторов - рабочих «Первая плавка».
В 1962 г. Рубцов приехал в Москву и поступил в Литературный институт им. М. Горького. В 1963-1964 гг. написал свои знаменитые стихотворения «Звезда полей», «Тихая моя родина...», «Я буду скакать по холмам задремавшей отчизны», «Русский огонек» и др.
Первый сборник стихов «Лирика» вышел в 1965 г. В 1967 г. выходит его книга «Звезда полей», в 1969 - «Душа хранит», в 1971 - «Зеленые цветы». Последняя из названных книг вышла в свет уже после смерти поэта.
Тот факт, что произведения Н. Рубцова вошли в школьные учебники по литературе в «окружении» русских поэтов - классиков, говорит о значимости его творчества.
Действительно, проанализируем текст его стихотворения «Березы»:
Я люблю, когда шумят берёзы,
Когда листья падают с берёз.
Слушаю – и набегают слёзы
На глаза, отвыкшие от слёз.
Всё очнётся в памяти невольно,
Отзовётся в сердце и в крови.
Станет как-то радостно и больно,
Будто кто-то шепчет о любви.
Только чаще побеждает проза,
Словно дунет ветер хмурых дней.
Ведь шумит такая же берёза
Над могилой матери моей.
На войне отца убила пуля,
А у нас в деревне у оград
С ветром и с дождём шумел, как улей,
Вот такой же жёлтый листопад…
Русь моя, люблю твои берёзы!
С первых лет я с ними жил и рос.
Потому и набегают слёзы
На глаза, отвыкшие от слёз.
(пос. Приютино, 1957)
Стихотворение "Берёзы" было написано в 1957 году, когда Николай Рубцов, проходя службу на флоте, находился в отпуске в селе Приютино Ленинградской области. Оно относится к ранней лирике, но, несмотря на относительную незрелость поэта, в стихах прослеживаются темы, которые впоследствии пройдут через все его произведения: тема Родины и тема его поколения.
Испытывая сильное влияние творчества Сергея Есенина с его "страной берёзового ситца", Рубцов соединяет образ России с картинами берёзовых рощ: "Я люблю, когда шумят берёзы…", "Русь моя, люблю твои берёзы!" Впоследствии образ "берёзовой Руси" мы встретим во многих произведениях поэта: "Счастье", "Северная берёза"(1957), "У знакомых берёз"(1968), "Под ветвями больничных берёз"(1970), "Ферапонтово"(1970), "Я умру, когда трещат берёзы"(1970).
Шум берёз и картина падающих осенних листьев вызывают у поэта щемящее чувство любви к своей родине и тоски по отчему дому: "слушаю – и набегают слёзы на глаза, отвыкшие от слёз".
Мать поэта умерла в самом начале войны, отец воевал на фронте, а после войны жил с другой семьёй. Известно, что поэт рос в детском доме, находившемся на родине его матери в селе Никольском, которое он и считал своей малой родиной. Поэтому мы видим по тексту стихотворения, что образ шумящих берёз "…отзовётся в сердце и крови", потому что - "с первых лет я с ними жил и рос".
Несмотря на то, что Николай Рубцов был сиротой при живом отце и с детства познал суровые стороны жизни, у поэта мы видим стремление быть, как все, не видеть в своей судьбе уникальности, а, напротив, отождествить её с судьбой многих детей военного времени: могила матери, "на войне отца убила пуля"… Таким образом, одиночество и страдания, вызванные отсутствием отчего крова, трансформируются, перерастая в болезненную любовь к Родине, её святыням, в способность находить счастье и удовлетворение в общении с природой как с близким человеком: "…когда шумят берёзы, когда листья падают с берёз… станет как-то радостно и больно, будто кто- то шепчет о любви."
Интересно, что использование такого приёма, как повторение слов: "шумит такая же берёза" и в последующем четверостишии: "шумел… такой же желтый листопад" даёт возможность поэту соединить несоединенные в жизни судьбы родителей, доведя тему сиротства до обобщения.
Читая стихотворение, мы ощущаем русскую душу поэта не только в открывающихся перед нами образах, но и благодаря тому, что поэт использует здесь песенный приём, характерный для русского фольклора – повторение одинаковых слов в начале и в конце текста стихотворения: "…набегают слёзы на глаза, отвыкшие от слёз". Этот приём будет часто применяться автором на протяжении всей его творческой жизни. Известно, что Николай Рубцов часто исполнял свои стихи под аккомпанемент гитары. Вероятно, отсюда и родился приём, который дает возможность придать произведению законченность, округлость, приближая к жанру народной песни.
В заключение можно сказать, что в небольшом, камерном произведении, написанном в самом начале творческого пути, мы видим рождение характерных черт, поэтических образов и приёмов, которые в дальнейшем проявятся со всей полнотой в творчестве незаурядного русского поэта, представителя "эпохи шестидесятых", приложившего много сил, "чтоб книгу Тютчева и Фета продолжить книгою Рубцова" ("Я переписывать не стану…").
Такой литературоведческий анализ несомненно содержит элемент субъективизма, и он также не позволяет дать необъективную сравнительную оценку этого стихотворения с произведениями других поэтов, тексты которых используются для раскрытия указанных тем.
Покажем, что такие несубъективные оценки можно производить с помощью информационных измерений.
Известно, что впервые числовые оценки поэтического текста выполнялись известным русским математиком Марковым А.А. в начале ХХ столетия. Сущность этих оценок сводилась к следующему: из романа Пушкина А.С. «Евгений Онегин» составлялся список всех слов, например, на начальную букву «а», затем, исходя из этого списка, подсчитывалась вероятность появления всех букв русского алфавита на втором месте после буквы «а», далее на третьем месте и т.д. По такой же схеме анализировались списки слов на другие начальные буквы.
Вероятностный процесс появления букв алфавита в определенных позициях слова Марков А.А. назвал случайным процессом, начинающимся с некоторого начального состояния. В указанном случае начальное состояние – это список слов на начальную букву «а».
В настоящее время в теории массового обслуживания такие случайные процессы стали называться цепями Маркова.
Следует заметить, что при анализе указанного произведения Маркову удалось накопить такой фактический материал по так называемым вероятностям перехода, который и по сей день служит надежной экспериментальной проверкой различных теорий массового обслуживания.
После исследований Маркова А.А. интерес к информационным измерениям текстов естественного языка возобновился только с установлением Шенноном следующей формулы для приближенных вычислений количественной меры информации
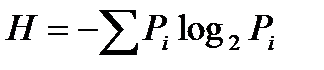 , (1)
, (1)
где через Pi обозначена вероятность или частота i-го события, а суммирование производится по всем значениям Рi.
Величина Н измеряется в битах и ее часто называют энтропией информации. Формулу (1) стали применять при анализе кодов, используемых при передаче сообщений, составленных на каком-либо естественном языке.
Сам Шеннон не дал строгих правил вычисления частоты рi применительно к различным ситуациям. Некоторые исследователи под рi стали подразумевать частоты появления букв алфавита в текстах естественного языка, а величину Н стали трактовать как энтропию одной буквы текста. Измерения такого толка описаны, например, в [5].
В [6] описаны информационные измерения на основе формулы (1) в текстах различных естественных языков, но для вычисления частот предложены специальные схемы по угадыванию букв неизвестного текста.
Описанные информационные измерения устанавливают числовые характеристики естественного языка, которые имеют непосредственное отношение к проблеме передачи информации по различным линиям связи.
Однако в языкознании имеется направление, в рамках которого проводятся частотные измерения, выявляющие индивидуальность стиля писателя. Например, в одинаковых по объему текстах различных писателей производится частотный анализ появления слов метаязыка русского языка [7]. Так, при идентификации авторства романа «Тихий дон» в одном из Норвежских университетов частотный анализ использовался наряду с другими экспертными оценками.
Для применения формулы (1) в частотных измерениях литературных текстов необходимо ей придать иное толкование по сравнению с толкованием в теории передачи сообщений.
Действительно, для определения количественной меры детерминированной информации используется комбинаторная формула
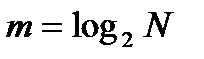 , (2)
, (2)
связывающая длину слова m с количеством N слов этой длинны, составленных из букв двоичного алфавита. Американский исследователь Л.Хартли в 1928г. отождествил максимальное количество информации Н с длиной слова m, т. е.
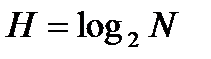 , (3)
, (3)
Предположим, что имеет место N слов как объем некоторой статистической выборки, состоящей из нескольких групп слов. Следуя [4], предположим, что в пределах каждой группы слова имеют одинаковую длину. Обозначим через ni объем каждой группы слов, тогда очевидно, что

По формуле (2) вычислим длину слова из группы n1, после будем иметь
 , (4)
, (4)
Теперь вычислим разность левых и правых частей в формулах (2) и (4):
 (5)
(5)
из (5) известно, что Н1 суть длина не идентифицированных слов. Аналогично можно составить следующие соотношения
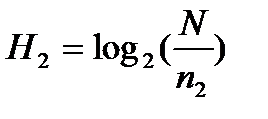 …,
…, 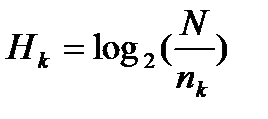 (6)
(6)
составим среднюю статистическую сумму
 ,
,
которую с учетом (5)-(6) перепишем так:
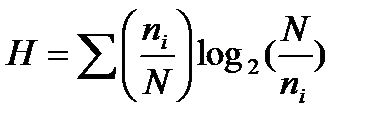 (7)
(7)
Если в каждой группе слов их число равно единице (n1=1) и число групп k равно N, то формула (7) переходит в формулу Хартли (3). В противном случае обозначим через рi частоту появления слов i-ой группы, которую определим общеизвестным способом
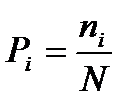 (8)
(8)
Теперь после подстановки (8) в (7), получим формулу Шеннона (1). Этот вывод формулы Шеннона впервые выполнен в [7], из которого следует, что Н есть статистическая средняя длина всех не идентифицированных слов, входящих в данную выборку N, а рi – частота, или вероятность появления этих слов.
Таблица 1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| а | б | в | г | д | е | ж | з | и | к | л | м | н | о | п | р | с |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | ||||||
| т | у | ф | х | ц | ч | ш | щ | э | ю | я |
В дальнейшем при использовании формулы (1) для расчета количественной меры информации поэтических текстов под рi будет подразумеваться частота появления слов по начальной букве русского алфавита. Процедуру такого расчета с использованием программ MicrosoftWord и MicrosoftExcel продемонстрируем на примере текста стихотворения Николая Рубцова «Березы». Для этого напишем программу на языке макрокоманд. Так как любая программа требует отладки, будем проводить её посредствам сравнения получающихся в процессе написания программы результатов с образцами, представленными в виде рисунков.
1. Включение компьютера и вход в систему. Результат выполнения представлен на рисунке 1.
Рис. 1.
2. Запуск программы MicrosoftWord.
Результат выполнения представлен на рисунке 2.
Рис. 2.
3. Открытие документа MicrosoftWord. Параметры: - имя файла: «Березы.doc». Результат выполнения представлен на рисунке 3.
Рис. 3.

4. Замена символов в документе MicrosoftWord. Параметры: - заменяемый символ: « »; - заменяющий символ: «^p». Результат выполнения представлен на рисунке 4.
Рис. 4.
5. Копирование в буфер обмена MicrosoftWord .
6. Запуск программы MicrosoftExcel.
Параметры: - рабочий стол. Результат выполнения представлен на рисунке 5.
Рис. 5.
7. Выбор активного листа.
Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 6.
Рис. 6.
 8. Вставка из буфера обмена MicrosoftExcel .
8. Вставка из буфера обмена MicrosoftExcel .
Параметры: - ячейка: A1. Результат выполнения представлен на рисунке 7.
Рис. 7.
9. Автозаполнение - формула.
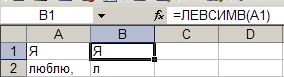 Параметры: - ячейка: B2; - данные: «=ЛЕВСИМВ(A1)» - конечная ячейка: B107. Результат выполнения частично представлен на рисунке 8. Рис. 8.
Параметры: - ячейка: B2; - данные: «=ЛЕВСИМВ(A1)» - конечная ячейка: B107. Результат выполнения частично представлен на рисунке 8. Рис. 8.
10. Занесение заголовка в ячейку.
Параметры: - ячейка: D1, E1, F1, G1, H1; - данные: «№ п/п», «Буква», «Кол-во», «Рi», «Pi*Log(Pi;2)». Результат выполнения частично представлен на рисунке 9.

Рис. 9.
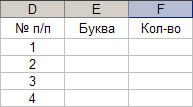
11. Автозаполнение - нумерация.
Параметры:- ячейка 1: «D2»; - ячейка 2: «D3»;
- конечная ячейка: «D29»; - данные 1: «1»;
- данные 2: «2»; Результат выполнения частично представлен на рисунке 10. Рис. 10.
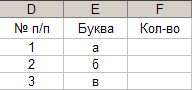 12. Занесение заголовка в ячейку.
12. Занесение заголовка в ячейку.
Параметры: - ячейка: E2-E29; - данные: «Таблица1». Результат выполнения частично представлен на рисунке 11. Рис. 11.
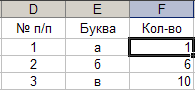 13. Автозаполнение - формула.
13. Автозаполнение - формула.
Параметры: - ячейка: F2; - данные: «=СЧЁТЕСЛИ(B:B;E2)» - конечная ячейка: F29. Результат выполнения частично представлен на рисунке 12. Рис. 12.
 14. Занесение заголовка в ячейку.
14. Занесение заголовка в ячейку.
Параметры: - ячейка: E30, G30; - данные: «N=», «H=». Результат выполнения частично представлен на рисунке 13. Рис. 13.
 15. Занесение формул в ячейку.
15. Занесение формул в ячейку.
Параметры: - ячейка: F30; - данные: «=СУММ(F2:F29)». Результат выполнения представлен на рисунке 14. Рис. 14.
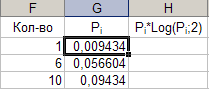
16. Автозаполнение - формула.
Параметры: - ячейка: G2; - данные: «=F2/F$30»; - конечная ячейка: G29. Результат выполнения частично представлен на рисунке 15. Рис. 15.
17. Автозаполнение - формула.
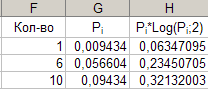 Параметры: - ячейка: H2; - данные: «=ЕСЛИ(G2=0;0;-G2*LOG(G2;2))»; - конечная ячейка: H29. Результат выполнения частично представлен на рисунке 16. Рис. 16.
Параметры: - ячейка: H2; - данные: «=ЕСЛИ(G2=0;0;-G2*LOG(G2;2))»; - конечная ячейка: H29. Результат выполнения частично представлен на рисунке 16. Рис. 16.
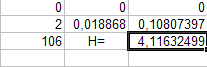 18. Занесение формул в ячейку.
18. Занесение формул в ячейку.
Параметры: - ячейка: H30; - данные: «=СУММ(H2:H29)». Результат выполнения представлен на рисунке 17. Рис. 17.
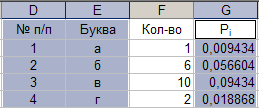 18. Активизация несвязанного диапазона ячеек.
18. Активизация несвязанного диапазона ячеек.
Параметры: - диапазон ячеек 1: «D1÷E29»; - диапазон ячеек 2: «G1÷G29». Результат выполнения представлен в таблице на рисунке 18. Рис. 18.
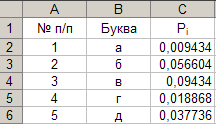
19. Копирование в буфер обмена.
Параметры: - ячейка-цель: «Лист2!A1». Результат выполнения представлен на рисунке 19.
Рис. 19.
20. Построение диаграммы .
Параметры: - диапазон данных: «C2÷C29»; - диапазон подписей: «B2÷B29»; - тип: «гистограмма»; - вид: «обычная гистограмма»; - название оси Х: « n »; - название оси Y : « Pi »; - размещение: «в отдельном листе». Результат выполнения представлен на рисунке 20.
Рис. 20.
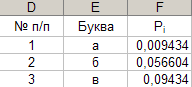 21. Копирование в буфер обмена.
21. Копирование в буфер обмена.
Параметры: - диапазон-источник: «A1÷C29»; - ячейка-цель: «D1». Результат выполнения представлен на рисунке 21. Рис. 21.
22. Сортировка данных.
Параметры: - диапазон: «E2÷F29»; - тип: «по возрастанию»; - сортировка: « Pi ». Результат выполнения частично представлен на рисунке 22.
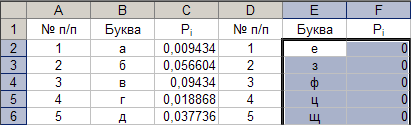
Рис. 22.
23. Построение диаграммы .
Параметры: - диапазон данных: «F2÷F29»; - диапазон подписей: «E2÷E29»; - тип: «гистограмма»; - вид: «обычная гистограмма»; - название оси Х: « n »; - название оси Y : « Pi »; - размещение: «в отдельном листе». Результат выполнения представлен на рисунке 23.
Рис. 23.
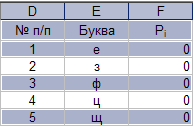 24. Активизация несвязанного диапазона ячеек.
24. Активизация несвязанного диапазона ячеек.
Параметры: - диапазон ячеек 1: «D1÷F1»; - диапазон ячеек 2: «не чётные строки из диапазона D2÷F29». Результат выполнения представлен в таблице на рисунке 24. Рис. 24.
25. Копирование в буфер обмена.
Параметры: - ячейка-цель: «G1».
Результат выполнения частично представлен на рисунке 25.

Рис. 25.
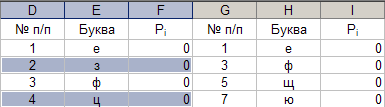 26. Активизация несвязанного диапазона ячеек.
26. Активизация несвязанного диапазона ячеек.
Параметры: - диапазон ячеек 1: «чётные строки из диапазона D2÷F29». Результат выполнения представлен в таблице на рисунке 26. Рис. 26.
27. Копирование в буфер обмена.
Параметры: - ячейка-цель: «G16».
Результат выполнения частично представлен на рисунке 27.
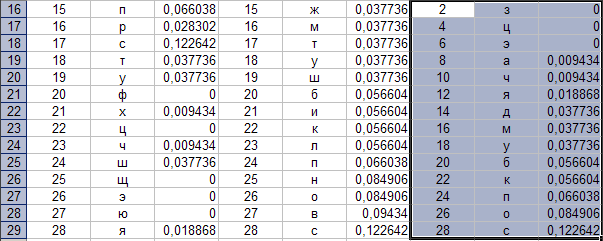
Рис. 27.
28. Сортировка данных.
Параметры: - диапазон: «G16÷I29»; - тип: «по убыванию»; - сортировка: «по столбцу I». Результат выполнения частично представлен на рисунке 28.
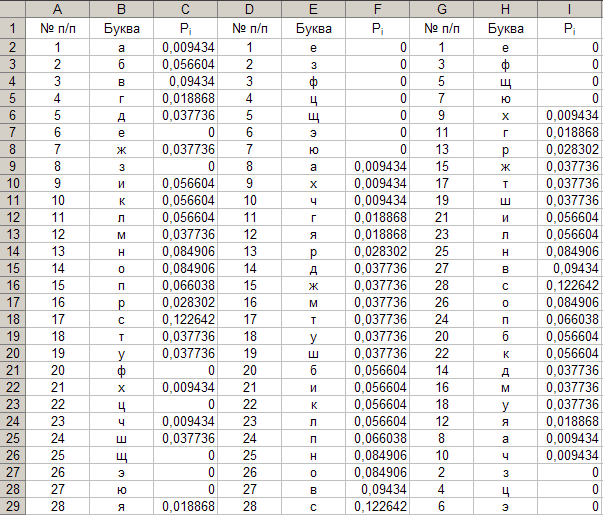
Рис. 28.
29. Построение диаграммы .
Параметры: - диапазон данных: «I2÷I29»; - диапазон подписей: «H2÷H29»; - тип: «гистограмма»; - вид: «обычная гистограмма»; - название оси Х: « n »; - название оси Y : « Pi »; - размещение: «в отдельном листе». Результат выполнения представлен на рисунке 29.
Рис. 29.
Для нормальной кривой распределения имеют физический смысл такие характеристики, как математическое ожидание х и среднее квадратичное отклонение s. Для вычисления этих величин в математической статистике имеют место следующие формулы
 ;
; 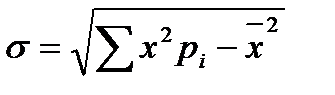
Рассчитаем эти характеристики для чего продолжим написание программы на языке макрокоманд.
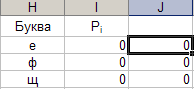 30. Автозаполнение - формула.
30. Автозаполнение - формула.
Параметры: - ячейка: J2; - данные: «=A2*I2»; - конечная ячейка: J29. Результат выполнения частично представлен на рисунке 30. Рис. 30.
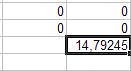 31. Занесение формул в ячейку.
31. Занесение формул в ячейку.
Параметры: - ячейка: J30; - данные: «=СУММ(J2:J29)». Результат выполнения представлен на рисунке 31. Рис. 31.
 32. Автозаполнение - формула.
32. Автозаполнение - формула.
Параметры: - ячейка: K2; - данные: «=(A2-J$30)*(A2-J$30)*I2»; - конечная ячейка: K29. Результат выполнения частично представлен на рисунке 32. Рис. 32.
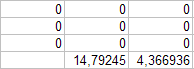 33. Занесение формул в ячейку.
33. Занесение формул в ячейку.
Параметры: - ячейка: K30; - данные: «=СУММ(K2:K29)^0,5». Результат выполнения представлен на рисунке 33. Рис. 33.
Для рассматриваемого стихотворения Рубцова эти числа оказались равными  =14,79245, σ =4,366936.
=14,79245, σ =4,366936.
Проделанные вычисления показали, что Н и σ, рассчитанные по кривой нормального распределения, оказываются близкими числами. Этот результат впервые получен в [8].
В Таблице 2 представлены результаты аналогичных расчетов над произведениями упомянутых авторов. Из этой таблицы следует, что кроме стихотворения «Видения на холме», все остальные имеют близкие значения величин энтропии информации.
Отсюда можно заключить, что отобранные стихотворения для изучения в школе имеют одинаковый качественный уровень.
Следует так же заметить, что при наборе стихотворного текста на клавиатуре компьютера, к работе зрительных рецепторов подключается моторика пальцев рук. Таким образом, активизируются несколько видов памяти, зрительная, моторная и ассоциативная. Возникающие, благодаря такой работе, дополнительные связи в коре головного мозга способствуют лучшему запоминанию стихотворных текстов и их дальнейшему осмыслению.
Таблица 2.
| Автор | Название (первая строка) | N | H, бит | χ | σ |
| Рубцов Н.М. | Березы | 106 | 4,116325 | 14,79245 | 4,366936 |
| Звезда полей | 81 | 3,847908 | 14,69136 | 3,667145 | |
| Тихая моя родина | 103 | 4,147141 | 14,70874 | 4,434269 | |
| Левитан | 48 | 3,763646 | 14,77083 | 3,536945 | |
| По дороге к морю | 109 | 4,231303 | 14,82569 | 4,717417 | |
| Видения на холме | 174 | 4,215583 | 14,74138 | 4,59345 | |
| Под ветвями больничных берез | 116 | 3,925454 | 14,66667 | 3,94888 | |
| В минуты музыки | 110 | 3,821215 | 14,76364 | 3,712209 | |
| А. Блок | Летний вечер | 50 | 3,721077 | 14,66 | 3,332327 |
| С. Есенин | Мелколесье. Степь и дали | 99 | 4,23653 | 14,65657 | 4,776122 |
| А. Ахматова | Перед весной бывают дни такие | 41 | 3,534892 | 14,82927 | 2,912567 |
| Б. Сологуб | Забелелся туман за рекой | 53 | 3,838506 | 14,83019 | 3,622445 |
По описанной выше схеме произведены расчеты сорока пяти стихотворений Николая Рубцова. Результаты этих расчетов систематизированы в таблице 3.
Таблица 3
| № | Названия стихотворения | Н бит | Число начальных букв с нулевыми частотами | Количество слов в стихотворении | Частоты слов на начальные буквы | ||
| в | н | с | |||||
| 1 | Элегия | 3,6294 | 9 | 70 | 0,0714 | 0,1 | 0,1 |
| 2 | Ось | 4,0043 | 7 | 86 | 0,0349 | 0,0349 | 0,0349 |
| 3 | На вокзале | 3,9064 | 8 | 125 | 0,144 | 0,08 | 0,072 |
| 4 | Весна на берегу Бии | 4,0055 | 5 | 131 | 0,1145 | 0,0763 | 0,1069 |
| 5 | Прощальная песня | 4,0215 | 6 | 182 | 0,0714 | 0,1264 | 0,1099 |
| 6 | В лесу | 3,1878 | 9 | 84 | 0,119 | 0,0833 | 0,1905 |
| 7 | Ветер всхлипывал словно дитя | 3,895 | 9 | 74 | 0,0811 | 0,054 | 0,126 |
| 8 | У церковных берез | 3,9637 | 6 | 130 | 0,0923 | 0,0692 | 0,0615 |
| 9 | В московском кремле | 7,1349 | 10 | 148 | 0,2143 | 0,2142 | 0,5357 |
| 10 | Поэзия | 3,4573 | 6 | 133 | 0,1061 | 0,0682 | 0,1061 |
| 11 | Сентябрь | 3,7171 | 11 | 62 | 0,0484 | 0,1613 | 0,129 |
| 12 | По дороге к морю | 8,2939 | 6 | 114 | 0,3333 | 0,1 | 0,2333 |
| 13 | Стоит жара | 4,0368 | 8 | 57 | 0,0877 | 0,0526 | 0,1754 |
| 14 | Плыть, плыть | 6,4871 | 6 | 84 | 0,1429 | 0,3214 | 0,2143 |
| 15 | Волнуется море | 4,1101 | 8 | 69 | 0,1449 | 0,058 | 0,1014 |
| 16 | Гость молчит и я ни слова | 3,7901 | 12 | 79 | 0,1013 | 0,0886 | 0,1138 |
| 17 | В пустыне | 3,7915 | 10 | 77 | 0,0909 | 0,039 | 0,1299 |
| 18 | Увлекаюсь нечаянно | 3,4473 | 14 | 50 | 0,02 | 0,04 | 0,08 |
| 19 | В горной деревне | 4,0075 | 9 | 80 | 0,075 | 0,05 | 0,1125 |
| 20 | Мечты | 3,7149 | 9 | 76 | 0,2027 | 0,1351 | 0,0676 |
| 21 | Видения на холме | 4,2156 | 3 | 174 | 0,1034 | 0,0862 | 0,0632 |
| 22 | Грани | 4,0147 | 8 | 70 | 0,0714 | 0,1286 | 0,1143 |
| 23 | По мокрым скверам проходит осень | 3,8397 | 9 | 93 | 0,0753 | 0,0968 | 0,1505 |
| 24 | В полях смеркалось. Близилась гроза | 3,6658 | 11 | 65 | 0,0615 | 0,0615 | 0,0462 |
| 25 | Привет Россия | 3,9456 | 9 | 114 | 0,1053 | 0,0877 | 0,1053 |
| 26 | В горнице | 3,8638 | 9 | 57 | 0,1053 | 0,0877 | 0,1403 |
| 27 | Родная деревня | 4,1048 | 6 | 66 | 0,0606 | 0,0606 | 0,0455 |
| 28 | Вологодский пейзаж | 4,1059 | 6 | 128 | 0,1094 | 0,0469 | 0,1016 |
| 29 | Далекое | 7,1822 | 7 | 85 | 0,3214 | 0,1786 | 0,4286 |
| 30 | На вокзале | 3,7422 | 8 | 123 | 0,1382 | 0,0732 | 0,065 |
| 31 | Старик | 3,7852 | 9 | 101 | 0,099 | 0,0693 | 0,0396 |
| 32 | Сапоги мои - скрип да скрип | 3,8066 | 9 | 125 | 0,064 | 0,048 | 0,072 |
| 33 | Памяти матери | 3,87 | 7 | 84 | 0,1309 | 0,0833 | 0,1905 |
| 34 | В сибирской деревне | 4,0113 | 6 | 90 | 0,1111 | 0,0778 | 0,1333 |
| 35 | Зимним вечерком | 3,9955 | 8 | 60 | 0,1 | 0,0667 | 0,05 |
| 36 | Меж болотных стволов красовался восток огнеликий | 3,9847 | 7 | 102 | 0,186 | 0,059 | 0,098 |
| 37 | Синенький платочек | 3,9445 | 4 | 89 | 0,1149 | 0,069 | 0,1724 |
| 38 | Острова свои оберегаем | 3,9407 | 9 | 82 | 0,1196 | 0,0652 | 0,0761 |
| 39 | А между прочим осень на дворе | 4,0818 | 5 | 121 | 0,1405 | 0,0577 | 0,0992 |
| 40 | Есть пора - души моей отрада | 4,2165 | 6 | 79 | 0,0633 | 0,0886 | 0,0506 |
| 41 | Старый конь | 3,9524 | 9 | 72 | 0,1389 | 0,0278 | 0,0694 |
| 42 | Прекрасное небо голубое | 4,0479 | 7 | 92 | 0,0543 | 0,0326 | 0,0326 |
| 43 | На реке Сухоне | 3,6389 | 10 | 112 | 0,1071 | 0,1607 | 0,1429 |
| 44 | Добрый Филя | 3,9008 | 9 | 56 | 0,0357 | 0,0179 | 0,0714 |
| 45 | Оттепель | 3,7292 | 8 | 113 | 0,0265 | 0,0177 | 0,0531 |
Анализ данных этой таблицы показывает, что количественная мера информации Н различна для каждого произведения и ее числовые значения для стихов Рубцова изменяются в довольно широких пределах. Все это означает, что числовые значения Н отражают литературные достоинства поэтических текстов.
Из таблицы 3 так же следует, что в стихах Рубцова частота появления слов на букву «в» лежит в приделах: 0,02≤р≥0,2143; соответственно на букву «н» – 0,0177≤р≥0,3214; и наконец на букву «с» –0,0349≤р≥0,5357.
Таблица 3 позволяет установить еще один из математических критериев, характеризующий индивидуальность творчества Н.Рубцова. Для этого изучим зависимость между энтропией информации Н и количеством слов в стихотворении N.
На плоскости НN построим совокупность точек, отражающих эту зависимость. Для этого в Excel набираем таблицу соответствия Н и N, заполняя столбцы А и В. Затем выделяем полученную таблицу и щелкаем на кнопке Мастер диаграмм. В открывшемся окошке выбираем точечную диаграмму и щелкаем на кнопке Далее. В шаге 3 называем ось х – Н, а ось y – N, на вкладке легенда убираем галочку Добавить легенду. В шаге 4 щелкаем мышью на слове «отдельном» и щелкаем на кнопке Готово.
Для дальнейших расчетов с использованием мастер-функции программы Excel переобозначим: y=H, x=N. Проверяем, связаны ли величины Н и N линейной зависимостью, т.е. имеет ли место функциональная зависимость. Для этого щелкаем правой клавишей мыши на одной из точек диаграммы. В открывшемся меню выбираем пункт – Добавить линию тренда. На вкладке Параметры ставим галочку около слов – Показывать уравнение на диаграмме и щелкаем на кнопке Ок. Чтобы придать диаграмме более удобный для просмотра вид делаем двойной щелчке на одной из осей диаграммы. В открывшемся окне выбираем вкладку Шкала и выставляем минимальное и максимальное значение так, чтобы данные занимали всю область построения диаграммы. Тоже самое делаем и для другой оси. В результате получится диаграмма, показанная на рис. 34.
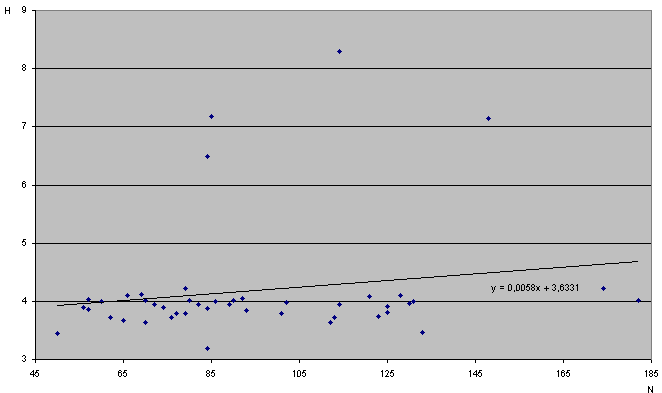
Рис. 34
Из рис. 34 становится очевидным, что между величинами Н и N нет функциональной зависимости. Степень отличия реальной связи между Н и N от линейной в математической статистики устанавливается так называемым коэффициентом корреляции r.
Возможности программы Excel позволяют вычислить эту величину. Для этого возвращаемся на лист с таблицей данных. Щелкаем в свободной ячейке и щелкаем на кнопке Мастер функций. В категории Статистические выбираем функцию КОРРЕЛ и щелкаем на кнопке Ок. в открывшемся окошке в графе Массив1 вводим - A2:A46, в графе Массив2 вводим - B2:B46 и нажимаем кнопку Ок. Получившееся в ячейке число и есть коэффициент корреляции.
Оказалось, что для произведений Н.Рубцова коэффициент корреляции r оказался равным 0,175974. полученное таким образом значение r и есть еще один критерий индивидуальности творчества данного поэта.
По всем буквам
Математизация любой науки связана со следующими двумя уровнями развития. Первый уровень обусловлен переходом науки к абстрактному осмысливанию накопленных фактов и к созданию языка для классификации эмпирических знаний. На втором уровне в языке науки все больше проявляется основное свойство, ради которого он создается, – возможность выражать внутренние закономерности, связи между отдельными фактами и явлениями, изучаемые данной наукой, а также служить орудием познавательной деятельности специалистов. Это требует развития не только выразительных средств языка, но и его исчисленческой стороны, т. е. различного рода формальных (математических) преобразований, которым можно подвергнуть те или иные слова, фразы и другие языковые конструкции.
Таким образом, следует считать, что язык любой науки состоит из двух частей. Первая, основная – это информативная часть языка, непосредственная информация, даже не классифицированная, а просто отобранная каким-то образом совокупность фактов, которые надлежит помнить, чтобы быть эрудированным в данной области знания. Вторая часть – это соответствующее исчисление, под которым, как правило, понимается сжатая форма выражения связей, позволяющих переходить от аксиом к следствиям, от них – к каким-то теоремам, фиксирующим знания в сжатой форме.
Язык математически вводится в язык конкретной науки для выполнения следующих функций:
§ Описание и систематизация знаний;
§ Получение результатов, сопоставимых с экспериментом;
§ Осуществление проверки исходных понятий и функциональных зависимостей между ними;
§ Формулировка законов науки, что дает средства не только для описания и проверки существующего положения, но и для различных видов предсказания.
Математизацию науки можно считать завершенной, если язык этой науки позволяет выполнить все перечисленные функции. К таким наукам можно отнести, прежде всего, физические: отнять у них математику – значит умертвить их.
Однако далеко не во всех науках до сих пор успешно применяются математические методы, хотя, казалось бы, они должны использоваться в любой науке, вступающей в этап абстрактного мышления, поскольку в этом случае наряду с информативной частью языка возникает его исчисленческая часть, позволяющая беспристрастно оценивать факты и явления.
Появление кибернетики и развитие вычислительной техники стимулировало формирование исчисленческой части языка в гуманитарных науках. Например, использование математических методов при изучении естественных языков способствовало возникновению математической лингвистики.
Рассмотрим поэтический текст Н. Рубцова «Видения на холме»:
Взбегунахолм
и упаду
в траву.
И древностью повеет вдруг из дола!
И вдруг картины грозного раздора
Я в этот миг увижу наяву.
Пустынный свет на звёздных берегах
И вереницы птиц твоих, Россия,
Затмит на миг
В крови и в жемчугах
Тупой башмак скуластого Батыя...
Россия, Русь - куда я ни взгляну...
3а все твои страдания и битвы
Люблю твою, Россия, старину,
Твои леса, погосты и молитвы,
Люблю твои избушки и цветы,
И небеса, горящие от зноя,
И шепот ив у омутной воды,
Люблю навек, до вечного покоя...
Россия, Русь! Храни себя, храни!
Смотри, опять в леса твои и долы
Со всех сторон нагрянули они,
Иных времён татары и монголы.
Они несут на флагах чёрный крест,
Они крестами небо закрестили,
И не леса мне видятся окрест,
А лес крестов
в окрестностях
России.
Кресты, кресты...
Я больше не могу
Я резко отниму от глаз ладони
И вдруг увижу: смирно на лугу
Траву жуют стреноженные кони.
Заржут они и где-то у осин
Подхватит эхо медленное ржанье,
И надо мной –
бессмертных звёзд Руси,
Спокойных звёзд безбрежное мерцанье.
В рамках информативной части языка об этом тексте можно сказать следующее.
Это стихотворение во многом программное, в нем сконцентрированы основные мотивы творчества Рубцова. Прежде всего - тема исторической, национальной памяти, помогающая воспроизвести в сознании события от времени Батыя до наших дней. 3десь и мотив духовной, нравственной крепости народа, сумевшего выстоять в тягчайших испытаниях, отстоять свою независимость, и призыв к современникам исполнять свой долг перед отечеством. Так протягивается нить от Пушкинского стихотворения «Клеветникам России», Лермонтовского «Бородино», Блоковских «Скифов» к стихотворению «Видения на холме» с его особым символическим историко-философским осмыслением новой эпохи. Для Рубцова важно не только то, что выражено словами, но и то, что в подтексте, не высказано, но напето самой мелодией души. Приглашая учиться высокому искусству гармонии у природы, поэт прекрасно понимал жгучую связь между человеком и родной природой, которая может, оборвавшись, привести к трагедии, не только экологической, но и нравственной. Отсюда и трагические тона, усиливающие внутренний драматизм его поэзии.
С вышесказанной оценкой текста «Видения на холме» согласится, прежде всего, человек, глубоко любящий родину, переживающий ее невзгоды и радующийся успехам своей страны. Для человека с иными взглядами анализируемый текст не вызовет никаких эмоций и может быть отнесен к обычной посредственности. Вполне очевидно, что оценка поэтических текстов информативным языком страдает субъективностью.
Возникает вопрос: можно ли найти формальные, не субъективные оценки поэтических текстов. С позиции исчисленческой части языка любой текст – это множество (набор) слов. Слова образуют группы слов по какому-либо признаку. В качестве такого признака можно выбрать, например, начальную букву слова. Если число всех слов в тексте обозначить через N1, а число слов на конкретную начальную букву – через ni, то можно определить величину
 (1),
(1),
которую назовем частотой появления слова на данную i-ю букву. В число niбудем включать и слова, состоящие из одной буквы.
По набору частот piможно вычислить энтропию информации по известной формуле Шеннона
 (2)
(2)
Величина Н1 известна также как количественная мера информации, и она измеряется в битах.
Впервые в [1] этот критерий был использован для количественных оценок поэтических текстов Н. Рубцова. Там же и дана технология обработки текста и проведения расчетов по (2) в программе MicrosoftExcel.
Рассчитанная по технологии [1] величина Н1 для текста «Видения на холме» оказалось равной 4,2077. Само по себе это число пока не о чем не говорит. Однако оказалось, что есть тексты других авторов, энтропия информации которых близка к вышеприведенному числу (см. таблица 1).
Таблица 1
| Автор | Название (первая строка) | N1 | Н1, бит |
| Рубцов Н. | Видения на холме | 174 | 4,2077 |
| Блок А. А. | В ресторане | 108 | 4,1897 |
| Есенин С. А. | Отговорила роща золотая | 233 | 4,2539 |
| Лермонтов М. Ю. | Бородино Завещание Пророк Родина Смерть поэта | 372 140 127 124 356 | 4,2169 4,1541 4,2091 4,0142 4,0900 |
| Некрасов Н. А. | Кому на Руси жить хорошо | 267 | 4,0119 |
| Пушкин А. С. | Кипренскому Цветок | 55 74 | 4,1177 4, 0646 |
| Фет А. А. | Ель рукавом мне тропинку завесила | 54 | 4,0298 |
| Цветаева М. И. | Стихи о Москве | 149 | 4, 1734 |
Возникает вопрос: что означают близкие числовые значения энтропии информации для текстов различных авторов? Ответ с формальной точки зрения таков: все тексты из таблицы 1 имеют примерно одинаковые средние статистические длины слов.
Вполне очевидно, что неформальный ответ на поставленный вопрос могут давать эксперты, занимающиеся оценкой поэтического творчества.
В [1] произведен расчет Н1 для сорока пяти поэтических текстов Н. Рубцова. Результаты этих расчетов, заимствованные из [1], воспроизведены в таблице 2. Оказалось, что числовые значения Н1 для текстов Н. Рубцова изменяются в широких пределах. Возможно, это объясняется и тем обстоятельством, что среди этих текстов есть ранние стихи, как правило, подражательные, более зрелые и, наконец, совершенные, выдвинувшие Н. Рубцова в число лучших поэтов.
Таблица 2
| № номер текст. | Название стихотворения | Колич. слов N1 | Н1 бит | Колич. букв N2 | H2 бит |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | Элегия | 70 | 3,6294 | 361 | 4,3116 |
| 2 | Ось | 86 | 4,0043 | 426 | 4,4513 |
| 3 | На вокзале | 125 | 3,9064 | 560 | 4,4802 |
| 4 | Весна на берегу Бии | 131 | 4,0055 | 634 | 4,5382 |
| 5 | Прощальная песня | 182 | 4,0215 | 783 | 4,5462 |
| 6 | В лесу | 84 | 3,1878 | 587 | 4,3346 |
| 7 | Ветер всхлипывал словно дитя | 74 | 3,8950 | 367 | 4,3763 |
| 8 | У церковных берез | 130 | 3,9637 | 703 | 4,4996 |
| 9 | В московском кремле | 148 | 7,1349 | 742 | 4,4231 |
| 10 | Поэзия | 133 | 3,4573 | 678 | 4,5084 |
| 11 | Сентябрь | 62 | 3,7171 | 292 | 4,4649 |
| 12 | По дороге к морю | 114 | 8,2939 | 504 | 4,6126 |
| 13 | Стоит жара | 57 | 4,0368 | 247 | 4,4342 |
| 14 | Плыть, плыть | 84 | 6,4871 | 392 | 4,4778 |
| 15 | Волнуется море | 69 | 4,1101 | 345 | 4,5217 |
| 16 | Гость молчит и я ни слова | 79 | 3,7901 | 358 | 4,4911 |
| 17 | В пустыне | 77 | 3,7915 | 277 | 4,4016 |
| 18 | Увлекаюсь нечаянно | 50 | 3,4473 | 285 | 4,2204 | ||
| 19 | В горной деревне | 80 | 4,0075 | 385 | 4,5289 | ||
| 20 | Мечты | 76 | 3,7149 | 370 | 4,4679 | ||
| 21 | Видения на холме | 174 | 4,2156 | 788 | 4,4618 | ||
| 21 | Грани | 70 | 4,0147 | 344 | 4,1788 | ||
| 23 | По мокрым скверам проходит осень | 93 | 3,8397 | 454 | 4,2117 | ||
| 24 | В полях смеркалось. Близилась гроза | 65 | 3,6658 | 359 | 4,1651 | ||
| 25 | Привет Россия | 114 | 3,9456 | 695 | 3,8839 | ||
| 26 | В горнице | 57 | 3,8638 | 278 | 4,3709 | ||
| 27 | Родная деревня | 66 | 4,1048 | 366 | 4,4437 | ||
| 28 | Вологодский пейзаж | 128 | 4,1059 | 644 | 4,4986 | ||
| 29 | Далекое | 85 | 7,1822 | 422 | 4,5458 | ||
| 30 | На вокзале | 123 | 3,7422 | 558 | 4,4782 | ||
| 31 | Старик | 101 | 3, 7852 | 487 | 4,4542 | ||
| 32 | Сапоги мои - скрип да скрип | 125 | 3,8066 | 587 | 4,4202 | ||
| 33 | Памяти матери | 84 | 3,8700 | 354 | 4,3806 | ||
| 34 | В сибирской деревне | 90 | 4,0113 | 519 | 4,4737 | ||
| 35 | Зимним вечерком | 60 | 3,9955 | 266 | 4,4054 | ||
| 36 | Журавли | 102 | 3,9847 |
| 4,4701 | ||
| 37 | Синенький платочек | 89 | 3,9445 | 521 | 4,1398 | ||
| 38 | Острова свои оберегаем | 82 | 3,9407 | 470 | 4,4129 |
| 39 | А между прочим осень на дворе | 121 | 4,0818 | 781 | 4,1676 | |
| 40 | Слез не лей … | 79 | 4,2165 |
| 4,4475 | |
| 41 | Старый конь | 72 | 3,9524 | 360 | 4,2452 | |
| 42 | Прекрасное небо голубое | 92 | 4,0479 | 419 | 4,4840 | |
| 43 | На реке Сухоне | 112 | 3,6389 | 577 | 4,3361 | |
| 44 | Добрый Филя | 56 | 3,9008 | 259 | 4,5050 | |
| 45 | Оттепель | 113 | 3,7292 |
| 4,4821 |
Одним из фундаментальнейших понятий математики является понятие меры. В данном случае определение меры сводится к установлению такого диапазона числовых значений Н1,который определит высокохудожественный или непоэтический текст безотносительно к тому – каким автором он написан. Таким образом можно установить числовую шкалу значений Н1, с помощью которой можно будет осуществлять безсубъективные оценки поэтических текстов.
В таблице 1 кроме текста Н. Рубцова представлены тексты классиков русской поэзии, поэтому возможно число четыре на указанной шкале будет соответствовать высокохудожественным поэтическим текстам.
При проведении информационных измерений в текстах русского языка, поэтический текст можно считать как набор (множество) букв русского алфавита. Каждый элемент этого множества (каждую букву) можно привести в соответствие с числами натурального ряда в результате чего получим конечное множество, над элементами которого можно производить измерения. Если общее число букв данного текста обозначить через N2, а через Ni – количество конкретной i-ой буквы, то можно рассчитать
 (3)
(3)
как частоту появления конкретной буквы в рассматриваемом поэтическом тексте.
При расчете энтропии информации не конкретизируется методика расчета частот, поэтому и к частотам (3) применима формула Шеннона. В данном случае энтропию информации обозначим через Н2 и ее будем рассчитывать по следующей формуле
 (4)
(4)
Вернемся снова к тексту «Видения на холме» и для него определим Н2 по формуле (4).
Таблица 3
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| а | б | в | г | д | е | ё | ж | з | и | й | к | л | м | н | о | п |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | |
| р | с | т | у | ф | х | ц | ч | ш | щ | ь | ы | ъ | э | ю | я |
 1. Включение компьютера и вход в систему. Результат выполнения представлен на рисунке 1.
1. Включение компьютера и вход в систему. Результат выполнения представлен на рисунке 1.
Рис. 1.

2. Запуск программы MicrosoftExcel. Результат выполнения представлен на рисунке 2.
Рис. 2.
3. Выбор активного листа.
Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 3. Рис. 3.
 4. Автозаполнение - нумерация.
4. Автозаполнение - нумерация.
Параметры:- ячейка 1: «A2»; - ячейка 2: «A3»;
- конечная ячейка: «A34»; - данные 1: «1»;
- данные 2: «2»; Результат выполнения частично представлен на рисунке 4. Рис. 4.
 5. Занесение заголовка в ячейку.
5. Занесение заголовка в ячейку.
Параметры: - ячейка: A1; - данные: «x».
Результат выполнения представлен на рисунке 5.
Рис. 5.
 6. Занесение заголовка в ячейку.
6. Занесение заголовка в ячейку.
Параметры: - ячейка: B1; - данные: «Буква».
Результат выполнения представлен на рисунке 6.
Рис. 6.
 7. Занесение заголовка в ячейку.
7. Занесение заголовка в ячейку.
Параметры: - ячейка: B2-B34; - данные: «Таблица3».
Результат выполнения частично представлен на рисунке 7. Рис. 7.

8. Подсчёт символов в документе MicrosoftWord. Параметры: - символ: «а»; - ячейка MSExcel: «C2». Результат выполнения представлен на рисунке 8. Рис. 8.
 Аналогичным, описанному в пункте 8 образом, следует подсчитать количество всех букв алфавита представленного в таблице 3. Результаты подсчёта следует заносить последовательно в ячейки C3-C34. Результат выполнения частично представлен на рисунке 9. Рис. 9.
Аналогичным, описанному в пункте 8 образом, следует подсчитать количество всех букв алфавита представленного в таблице 3. Результаты подсчёта следует заносить последовательно в ячейки C3-C34. Результат выполнения частично представлен на рисунке 9. Рис. 9.
 9. Занесение заголовка в ячейку.
9. Занесение заголовка в ячейку.
Параметры: - ячейка: C1; - данные: «Кол-во».
Результат выполнения частично представлен на рисунке 10. Рис. 10.

10. Занесение формул в ячейку.
Параметры: - ячейка: С35; - данные: «=СУММ(C2:C34)». Результат выполнения представлен на рисунке 11. Рис. 11.
 11. Занесение заголовка в ячейку.
11. Занесение заголовка в ячейку.
Параметры: - ячейка: B35; - данные: «N2=».
Результат выполнения частично представлен на рисунке 12. Рис. 12.
 12. Занесение заголовка в ячейку.
12. Занесение заголовка в ячейку.
Параметры: - ячейка: D1; - данные: «Pi».
Результат выполнения представлен на рисунке 13. Рис. 13.
 13. Автозаполнение - формула.
13. Автозаполнение - формула.
Параметры: - ячейка: D2; - данные: «=C2/$C$35» - конечная ячейка: D34. Результат выполнения частично представлен в таблице на рисунке 14. Рис. 14.
14. Автозаполнение - формула.
 Параметры: - ячейка: E2; - данные: «=ЕСЛИ(D2=0;0;-D2*LOG(D2;2))» - конечная ячейка: E34. Результат выполнения частично представлен в таблице на рисунке 15. Рис. 15.
Параметры: - ячейка: E2; - данные: «=ЕСЛИ(D2=0;0;-D2*LOG(D2;2))» - конечная ячейка: E34. Результат выполнения частично представлен в таблице на рисунке 15. Рис. 15.
15. Занесение заголовка в ячейку.
 Параметры: - ячейка: D35; - данные: «H2=».
Параметры: - ячейка: D35; - данные: «H2=».
Результат выполнения частично представлен на рисунке 16. Рис. 16.
 16. Занесение формул в ячейку.
16. Занесение формул в ячейку.
Параметры: - ячейка: E35; - данные: «=СУММ(E2:E34)». Результат выполнения представлен на рисунке 17. Рис. 17.
 17. Активизация диапазона ячеек.
17. Активизация диапазона ячеек.
Параметры: - диапазон: A1÷D34. Результат выполнения частично представлен на рисунке 18. Рис. 18.
18. Копирование в буфер обмена.
 Параметры: - ячейка-источник: «A1÷D34»; - ячейка-цель: «Лист2! A 2». Результат выполнения частично представлен на рисунке 19. Рис. 19.
Параметры: - ячейка-источник: «A1÷D34»; - ячейка-цель: «Лист2! A 2». Результат выполнения частично представлен на рисунке 19. Рис. 19.
 19. Активизация диапазона ячеек.
19. Активизация диапазона ячеек.
Параметры: - диапазон: «B1÷D1». Результат выполнения частично представлен на рисунке 20. Рис. 20.
 20. Копирование в буфер обмена.
20. Копирование в буфер обмена.
Параметры: - ячейка-источник: «B1÷D1»; - ячейка-цель: «Лист2! B 1». Результат выполнения представлен на рисунке 21. Рис. 21.
 21. Выбор активного листа.
21. Выбор активного листа.
Параметры: - лист: «Лист2». Результат выполнения представлен на рисунке 22. Рис. 22.
 22. Занесение заголовка в ячейку.
22. Занесение заголовка в ячейку.
Параметры: - ячейка: A1; - данные: «№ буквы».
Результат выполнения частично представлен на рисунке 23. Рис. 23.
 23. Активизация диапазона ячеек.
23. Активизация диапазона ячеек.
Параметры: - диапазон: «A1÷D34». Результат выполнения частично представлен на рисунке 24. Рис. 24.
24. Копирование в буфер обмена.
Параметры: - ячейка-источник: «A1÷D34»; - ячейка-цель: «E1». Результат выполнения представлен на рисунке 25.

Рис. 25.
 25. Сортировка данных.
25. Сортировка данных.
Параметры: - диапазон: «E1÷H34»; - тип: «по возрастанию»; - сортировка: «Pi». Результат выполнения частично представлен на рисунке 26.
Рис. 26.
 26. Активизация диапазона ячеек.
26. Активизация диапазона ячеек.
Параметры: - диапазон: «E1÷H1». Результат выполнения частично представлен на рисунке 27. Рис. 27.
 27. Копирование в буфер обмена.
27. Копирование в буфер обмена.
Параметры: - ячейка-источник: «E1÷H1»; - ячейка-цель: «I1». Результат выполнения представлен на рисунке 28. Рис. 28.
 28. Активизация диапазона ячеек.
28. Активизация диапазона ячеек.
Параметры: - диапазон: «E2÷E34». Результат выполнения частично представлен на рисунке 29. Рис. 29.
 29. Копирование в буфер обмена.
29. Копирование в буфер обмена.
Параметры: - ячейка-источник: «E2÷E34»; - ячейка-цель: «I2». Результат выполнения представлен на рисунке 30. Рис. 30.
 30. Активизация диапазона ячеек.
30. Активизация диапазона ячеек.
Параметры: - диапазон: «F2÷H2». Результат выполнения частично представлен на рисунке 31. Рис. 31.
 31. Копирование в буфер обмена.
31. Копирование в буфер обмена.
Параметры: - ячейка-источник: «F2÷H2»; - ячейка-цель: «J34». Результат выполнения представлен на рисунке 32. Рис. 32.
 32. Активизация диапазона ячеек.
32. Активизация диапазона ячеек.
Параметры: - диапазон: «F3÷H3». Результат выполнения частично представлен на рисунке 33. Рис. 33.
33. Копирование в буфер обмена.
 Параметры: - ячейка-источник: «F3÷H3»; - ячейка-цель: «J2». Результат выполнения представлен на рисунке 34. Рис. 34.
Параметры: - ячейка-источник: «F3÷H3»; - ячейка-цель: «J2». Результат выполнения представлен на рисунке 34. Рис. 34.
Аналогично повторим шаги 30-33 для оставшихся диапазонов с F4÷H4 до F34÷H34. Вставку скопированных диапазонов следует производить в ячейки cJ4 до J34 соответственно. Результат выполнения частично представлен на рисунке 35.

Рис. 35.
34. Построение диаграммы .
Параметры: - диапазон данных: «L2÷L34»; - диапазон подписей: «J2÷J34»; - тип: «гистограмма»; - вид: «обычная гистограмма»; - название оси Х: «буква»; - название оси Y : «Pi»; - размещение: «в отдельном листе». Результат выполнения представлен на рисунке 36.
Рис. 36. Гистограмма нормального распределения частот.
Гистограмма нормального распределения частот иллюстрирует процесс группирования частот относительно максимальной частоты. Характер такой группировки может также характеризовать индивидуальность текста.
Действительно, гистограмма на рис. 36 представляет распределение частот букв русского алфавита для текста «Видения на холме». Однако из сочетания букв образуются такие составляющие слова, как слоги и корни. Поэтому представляется реальным создание определенного алгоритма, по которому из частотного распределения букв можно определить частоты появления определенных слогов и корней.
В таблице 2 представлены рассчитанные по вышеуказанной технологии величины Н2 для различных текстов Н. Рубцова. Диапазон изменения чисел Н2 оказался меньшим по сравнению с диапазоном Н1. Однако оказались такие тексты, для которых числовые значения Н1 и Н2 близки. Например, текст «Видения на холме». Возможно, этот факт служит еще одним доказательством того, что число четыре на числовой шкале соответствует высоко художественным текстам.
Для каждого из текстов из таблицы 2 были построены гистограммы распределения частот букв в порядке возрастания частоты. Эти гистограммы строились так же как и гистограммы на рис. 16. Из указанных гистограмм оказалось возможным получить для каждой из букв предельные значения частот, которые имеют место в текстах из таблицы 2.
Таблица 4 иллюстрирует значения предельных частот для каждой из букв русского алфавита.
Оказалось, что существуют такие поэтические тексты Н. Рубцова, в которых отсутствуют некоторые буквы алфавита. Это тексты, для которых Pmin=0. В данном случае к указанным буквам относятся следующие: ё, ф, х, ц, ш, щ, ъ, э, ю (см. таблицу 4). Кроме того, можно выделить буквы, для которых имеет место закон устойчивости частот.
Таблица 4
Буква
Экстремальные
Буква
Экстремальные
Частоты
Частоты
Pmax
Pmin
Pmax
Pmin
а
0,1015
0,0374
п
0,0528
0,0081
б
0,0406
0,0027
р
0,0651
0,0222
в
0,0683
0,0028
с
0,1022
0,0232
г
0,1922
0,0019
т
0,3036
0,0051
д
0,0612
0,0134
у
0,0665
0,0044
е
0,1187
0,0055
ф
0,0193
0
ё
0,2026
0
х
0,0355
0
ж
0,0364
0,0014
ц
0,0137
0
з
0,0347
0,0022
ч
0,0324
0,0029
и
0,1005
0,0246
ш
0,0167
0
й
0,0445
0,0051
щ
0,0156
0
к
0,0583
0,0156
ь
0,0459
0,0019
л
0,2265
0,0189
ы
0,242
0,0022
м
0,0765
0,0134
ъ
0,0036
0
н
0,1228
0,0338
э
0,0075
0
о
0,1833
0,0363
ю
0,0324
0
я
0,0351
0,0056
К таким буквам следует отнести только те, у которых предельные частоты различаются в одном и том же числовом знаке после запятой. Данные таблицы 6 позволяют к указанным буквам отнести следующие: д, к, м, р.
Для этих согласных характер изменения частот в зависимости от номера N текста иллюстрирует таблица 5. Заметим, что нумерация текстов Н. Рубцова в таблице 5 совпадает с их нумерацией в таблице 2. Построим гистограммы распределения частот для букв д, к, м, р.
Таблица 5
| N номер текста |
Частота появления букв | N номер текста |
Частота появления букв | ||||||
|
| д | к | м | р | 23 | 0,0176 | 0,0463 | 0,0441 | 0,0529 |
| 1 | 0,036 | 0,036 | 0,0249 | 0,0305 | 24 | 0,0334 | 0,039 | 0,0251 | 0,0418 |
| 2 | 0,0305 | 0,0446 | 0,054 | 0,0563 | 25 | 0,0173 | 0,0259 | 0,0331 | 0,0317 |
| 3 | 0,0286 | 0,0161 | 0,0321 | 0,0411 | 26 | 0,0612 | 0,0252 | 0,0432 | 0,036 |
| 4 | 0,0221 | 0,0363 | 0,0315 | 0,0599 | 27 | 0,0383 | 0,0355 | 0,0164 | 0,0464 |
| 5 | 0,0409 | 0,0498 | 0,0396 | 0,0434 | 28 | 0,0311 | 0,0342 | 0,0404 | 0,0559 |
| 6 | 0,0341 | 0,0409 | 0,0221 | 0,0443 | 29 | 0,0237 | 0,0379 | 0,0355 | 0,0355 |
| 7 | 0,0327 | 0,0245 | 0,0436 | 0,0381 | 30 | 0,0287 | 0,0161 | 0,0323 | 0,0412 |
| 8 | 0,037 | 0,0398 | 0,0299 | 0,0441 | 31 | 0,0513 | 0,0493 | 0,0287 | 0,037 |
| 9 | 0,035 | 0,0337 | 0,0391 | 0,0445 | 32 | 0,0562 | 0,0545 | 0,0221 | 0,0511 |
| 10 | 0,031 | 0,0487 | 0,0398 | 0,0413 | 33 | 0,0254 | 0,0226 | 0,0565 | 0,0367 |
| 11 | 0,024 | 0,0377 | 0,0171 | 0,0651 | 34 | 0,0289 | 0,0578 | 0,0193 | 0,0385 |
| 12 | 0,0278 | 0,0298 | 0,0575 | 0,0496 | 35 | 0,0338 | 0,0451 | 0,0489 | 0,0602 |
| 13 | 0,0202 | 0,0567 | 0,0324 | 0,0445 | 36 | 0,0282 | 0,0465 | 0,0183 | 0,0548 |
| 14 | 0,0357 | 0,0204 | 0,0765 | 0,051 | 37 | 0,0134 | 0,0403 | 0,0134 | 0,0345 |
| 15 | 0,0377 | 0,0493 | 0,0464 | 0,0493 | 38 | 0,0447 | 0,0404 | 0,0383 | 0,0404 |
| 16 | 0,0363 | 0,0391 | 0,0503 | 0,0475 | 39 | 0,0192 | 0,0282 | 0,0282 | 0,0435 |
| 17 | 0,0144 | 0,0542 | 0,0361 | 0,0469 | 40 | 0,0453 | 0,0283 | 0,034 | 0,0482 |
| 18 | 0,0316 | 0,0281 | 0,0175 | 0,0632 | 41 | 0,0417 | 0,0583 | 0,0222 | 0,0222 |
| 19 | 0,0338 | 0,0286 | 0,0338 | 0,0571 | 42 | 0,0263 | 0,0286 | 0,031 | 0,0597 |
| 20 | 0,0297 | 0,027 | 0,0514 | 0,0432 | 43 | 0,0399 | 0,0156 | 0,0676 | 0,0433 |
| 21 | 0,0266 | 0,0241 | 0,0254 | 0,0609 | 44 | 0,0502 | 0,027 | 0,027 | 0,0425 |
| 22 | 0,0349 | 0,0349 | 0,0407 | 0,064 | 45 | 0,0354 | 0,0314 | 0,0511 | 0,0413 |
 35. Выбор активного листа.
35. Выбор активного листа.
Параметры: - лист: «Лист3». Результат выполнения представлен на рисунке 37. Рис. 37.
36. Занесение заголовка в ячейку.
 Параметры: - ячейка: A1; - данные: «Номер текста».
Параметры: - ячейка: A1; - данные: «Номер текста».
Результат выполнения частично представлен на рисунке 38. Рис. 38.
37. Объединение ячеек.
 Параметры: : - диапазон: «B1÷E1». - данные: «Частота появления букв». Результат выполнения частично представлен на рисунке 39. Рис. 39.
Параметры: : - диапазон: «B1÷E1». - данные: «Частота появления букв». Результат выполнения частично представлен на рисунке 39. Рис. 39.
38. Занесение заголовка в ячейку.
 Параметры: - ячейка: B1; - данные: «Частота появления букв». Результат выполнения частично представлен на рисунке 40. Рис. 40.
Параметры: - ячейка: B1; - данные: «Частота появления букв». Результат выполнения частично представлен на рисунке 40. Рис. 40.
 39. Автозаполнение - нумерация.
39. Автозаполнение - нумерация.
Параметры:- ячейка 1: «A3»;
- ячейка 2: «A4»; - конечная ячейка: «A47»; - данные 1: «1»; - данные 2: «2»; Результат выполнения частично представлен на рисунке 41. Рис. 41.
 40. Занесение заголовка в ячейку.
40. Занесение заголовка в ячейку.
Параметры: - ячейка: B2; - данные: «д». Результат выполнения частично представлен на рисунке 42. Рис. 42.
 41. Занесение заголовка в ячейку.
41. Занесение заголовка в ячейку.
Параметры: - ячейка: C2; - данные: «к». Результат выполнения частично представлен на рисунке 43. Рис. 43.
 42. Занесение заголовка в ячейку.
42. Занесение заголовка в ячейку.
Параметры: - ячейка: D2; - данные: «м». Результат выполнения частично представлен на рисунке 44. Рис. 44.
 43. Занесение заголовка в ячейку.
43. Занесение заголовка в ячейку.
Параметры: - ячейка: E2; - данные: «р». Результат выполнения частично представлен на рисунке 45. Рис. 45.
44. Занесение десятичных дробей в диапазон ячеек.
Параметры: - диапазон ячеек: B3¸B47; - данные: «Таблица 7.Столбец “д”».
45. Занесение десятичных дробей в диапазон ячеек.
Параметры: - диапазон ячеек: C3¸C47; - данные: «Таблица 7.Столбец “к”».
46. Занесение десятичных дробей в диапазон ячеек.
Параметры: - диапазон ячеек: D3¸D47; - данные: «Таблица 7.Столбец “м”».
47. Занесение десятичных дробей в диапазон ячеек.
Параметры: - диапазон ячеек: E3¸E47; - данные: «Таблица 7.Столбец “р”».
Результат выполнения пунктов 44-47 частично представлен на рисунке 46.

Рис. 46.
 48. Активизация диапазона ячеек.
48. Активизация диапазона ячеек.
Параметры: - диапазон: «A2÷B47». Результат выполнения частично представлен на рисунке 47. Рис. 47.
 49. Копирование в буфер обмена.
49. Копирование в буфер обмена.
Параметры: - ячейка-источник: «A2÷B47»; - ячейка-цель: «F1». Результат выполнения представлен на рисунке 48. Рис. 48.
50. Сортировка данных.
 Параметры: - диапазон: «G1÷G46»; - тип: «по возрастанию»; - сортировка: «д». Результат выполнения частично представлен на рисунке 49.
Параметры: - диапазон: «G1÷G46»; - тип: «по возрастанию»; - сортировка: «д». Результат выполнения частично представлен на рисунке 49.
Рис. 49.
51. Построение диаграммы .
Параметры: - диапазон данных: «G2÷G46»; - диапазон подписей: «F2÷F46»; - тип: «гистограмма»; - вид: «обычная гистограмма»; - название оси Х: «x»; - название оси Y : «P5»; - размещение: «в отдельном листе». Результат выполнения представлен на рисунке 50.
Рис. 50. Закон распределения буквы «д» в порядке возрастания частоты.
 52. Активизация ячейки.
52. Активизация ячейки.
 Параметры: - ячейка: «G2 Результат выполнения частично представлен на рисунке 51. Рис. 51.
Параметры: - ячейка: «G2 Результат выполнения частично представлен на рисунке 51. Рис. 51.
53. Копирование в буфер обмена.
Параметры: - ячейка-источник: «G2»; - ячейка-цель: «H2». Результат выполнения представлен на рисунке 52. Рис. 52.
 54. Активизация ячейки.
54. Активизация ячейки.
Параметры: - ячейка: «G46» Результат выполнения частично представлен на рисунке 53. Рис. 53.
 55. Копирование в буфер обмена.
55. Копирование в буфер обмена.
Параметры: - ячейка-источник: «G46»; - ячейка-цель: «H3». Результат выполнения представлен на рисунке 54. Рис. 54.
Аналогичным образом необходимо последовательно скопировать наименьшие и наибольшие значения частот появления буквы «д». Вставлять скопированные значения следует в ячейки с H4 по H47. Результат выполнения частично представлен на рисунке 55.

Рис. 55
56. Построение диаграммы .
Параметры: - диапазон данных: «H2÷H46»; - диапазон подписей: «F2÷F46»; - тип: «гистограмма»; - вид: «обычная гистограмма»; - название оси Х: «x»; - название оси Y : «P5»; - размещение: «в отдельном листе». Результат выполнения представлен на рисунке 56.
Рис. 56. Закон устойчивости частот для буквы «д» (Р5).
Аналогичным образом, указанным в пунктах 48-56, следует построить диаграммы, иллюстрирующие закон устойчивости частот для букв «к», «м» и «р». Результаты выполнения представлены на рисунках 57-62.
Рис. 57. Закон распределения буквы «к» в порядке возрастания частоты.
Рис. 58. Закон устойчивости частот для буквы «к» (Р12).
Рис. 59. Закон распределения буквы «м» в порядке возрастания частоты.
Рис. 60. Закон устойчивости частот для буквы «м» (Р14).
Рис. 61. Закон распределения буквы «р» в порядке возрастания частоты.
Рис. 62. Закон устойчивости частот для буквы «р» (Р18).
На гистограммах, представленных на рисунках 50, 56, 57 - 62 по оси абсцисс отложен номер  текста, который может и не совпадать с номером того же текста в таблице 2; а по оси ординат дается значение частоты появления данной буквы в стихотворении, рассматриваемого номера. При построении указанных гистограмм тексты перенумерованы так, что поведение частот носит колебательный характер, а с ростом номера частоты появления букв стремятся к средним частотам равным
текста, который может и не совпадать с номером того же текста в таблице 2; а по оси ординат дается значение частоты появления данной буквы в стихотворении, рассматриваемого номера. При построении указанных гистограмм тексты перенумерованы так, что поведение частот носит колебательный характер, а с ростом номера частоты появления букв стремятся к средним частотам равным
 (5).
(5).
Значения средних частот, рассчитанных по (5) предоставляются таблицей 6.
Таблица 6
| Буква | Pmax | Pmin | ∆ |
| д | 0,061 | 0,013 | 0,048 |
| к | 0,058 | 0,016 | 0,043 |
| м | 0,077 | 0,013 | 0,063 |
| р | 0,065 | 0,022 | 0,043 |
Представленные таким образом колебательные поведения частот являются графической формой представления закона устойчивости частот.
| Таблица 7 | ||
| Буква | Число текстов n | Частота |
| ъ ф э | 40 36 20 | 0,8899 0,8000 0,4444 |
| щ ц ю | 20 15 8 | 0,4444 0,3333 0,1778 |
| ё х | 4 1 | 0,0889 0,0222 |
Вполне очевидно, что закон устойчивости частот для букв, указанных в таблицах 5 и 6, определяет индивидуальность поэтических произведений Н. Рубцова. Он как бы определяет набор словесного материала, который инвариантен для всех произведений рассматриваемого поэта.
Уже отмечалось, что среди рассматриваемых текстов (табл. 2) были и такие, в которых некоторые буквы не встречаются вообще. В таблице 7 приводятся эти буквы и число n текстов, в которых они не встречаются. Так как всего рассмотрено сорок пять текстов Н. Рубцова, то по формуле
 (6)
(6)
можно вычислить частоту появления текстов, в которых данные буквы отсутствуют. Результаты расчетов по (6) приведены в таблице 7.
Оказалось, что одной из редко встречающихся букв оказалась буква «ф» (см. табл. 7). За разъяснением этого обстоятельства обратимся к исследованиям выдающегося советского филолога Льва Васильевича Успенского (1900 – 1990). В его научно-занимательной книге [3] отмечается, что в поэтических произведениях Пушкина, Лермонтова, Крылова и других русских классиков буква «ф» почти не встречается. Обнаруживается и другое – каждое слово русского языка, в котором в начале, на конце или в середине пишется буква «ф», на поверку оказывается словом не исконно русским, а пришедшим к нам из других языков. По мнению Успенского, редкость буквы «ф» в русской литературе не случайность. Она – свидетельство глубокой народности, высокой чистоты русского языка у наших великих писателей.
Следовательно, указанная традиция великих русских классиков сохранена и в творчестве Н. Рубцова.
В настоящее время наметилась тенденция изучения поэтических текстов методами паралингвистики [3]. В этих исследованиях паралингвистические интонации, обнаруженные на основе частотного анализа буквосочетаний, обобщаются в модели эмоционально выразительных интонаций поэта.
Несомненно, что применение информационных технологий может активизировать исследования в паралингвистике.
Добавление слайдов
4. Щелкните на Вкладки слайды. Чтобы вставить новый слайд, нажмите клавишу Enter. Новый слайд появляется на вкладке Слайды под титульным слайдом. Кроме того, в правой части окна появляется новая область задач – Макеты слайдов. Если эту область задач не отключить, она появляется при каждой вставке нового слайда. Пока выключите ее: в нижней части области задач снимите флажок Показывать при вставке слайдов. Затем нажмите клавиши CTRL+F1, чтобы закрыть область задач. В добавленном слайде Заполнители расположены иначе, нежели на Титульном слайде. Вместо выровненных по центру заголовка и подзаголовка заполнитель заголовка этого слайда расположен вверху, а остальное место на слайде занято заполнителем основного текста с маркерами.
Это пример того, как могут различаться макеты слайдов. В первом слайде презентации использован макет титульного слайда, а в последующих – введенный заголовок и макет основного текста. Область задач Макеты слайдов, которую вы только что закрыли, обеспечивает работу с макетами.
Эскиз добавленного слайда на вкладке Слайды все еще выделен.
5. Щелкните правой кнопкой мыши выделенный эскиз и в контекстном меню выберите команду Создать слайд.
Появится третий эскиз слайда.
Еще один способ вставки – с помощью панели инструментов Форматирование, расположенной в верхней части окна PowerPoint. На этой панели имеются кнопки Полужирный  , Курсив
, Курсив  и другие кнопки форматирования. Кроме того, на ней расположена кнопка Создать слайд
и другие кнопки форматирования. Кроме того, на ней расположена кнопка Создать слайд  Если кнопка Создать слайд отсутствует, щелкните стрелку на правом краю панели. Кнопка Создать слайд появится в группе кнопок в верхней части меню. Нажмите ее.
Если кнопка Создать слайд отсутствует, щелкните стрелку на правом краю панели. Кнопка Создать слайд появится в группе кнопок в верхней части меню. Нажмите ее.

| Область задач |
| Эскиз слайда |
Выбор шаблона оформления
1. Для выбора шаблона оформления в контекстном меню выберите команду Конструктор. В области задач Дизайн слайда выберите Шаблоны оформления.


На вкладке Слайды выберите эскиз любого слайда, щелкните его правой кнопкой мыши и выберите нужный шаблон оформления. В качестве примера, выберите:
2. Чтобы применить другой шаблон оформления, прокрутите область задач так, чтобы появился раздел Доступно для использования. В нем находятся шаблоны, автоматически установленные вместе с программой PowerPoint. Обнаружив нужный шаблон, щелкните его (а не стрелку, которая появляется на нем). В этом случае шаблон будет применен ко всем слайдам.
Все эскизы слайдов на вкладке Слайды изменятся в соответствии с 
этим шаблоном. Тогда Титульный слайд будет иметь вид:
3. . Если требуется применить другой шаблон (для все слайдов), достаточно щелкнуть другой эскиз шаблона в Шаблонах оформления.
 4. Если требуется применить шаблон оформления только к нескольким (но не всем) слайдам, выделите их на вкладке Слайды (выбирайте слайды, удерживая клавишу CTRL), а затем щелкните нужный шаблон оформления. В каждом шаблоне оформления имеется меню, его стрелка появляется, когда на шаблон наведен указатель. Щелкните стрелку, раскроется меню, команды которого определяют, как будет применен шаблон. Для примера ко второму слайду примените
4. Если требуется применить шаблон оформления только к нескольким (но не всем) слайдам, выделите их на вкладке Слайды (выбирайте слайды, удерживая клавишу CTRL), а затем щелкните нужный шаблон оформления. В каждом шаблоне оформления имеется меню, его стрелка появляется, когда на шаблон наведен указатель. Щелкните стрелку, раскроется меню, команды которого определяют, как будет применен шаблон. Для примера ко второму слайду примените
Создание фона
В области задач Дизайн слайда выберите Цветовая схема
Оформление с помощью команды Цветовая схема слайда:


Формат _ Оформление слайда _Дизайн слайдов _ Цветовые схемы – панель справа будет иметь такой вид:
Заполните второй слайд по образцу:


Выберите нужную цветовую схему и примените ее к слайду (см. пункт 4 из Выбора шаблона оформления). Тогда, слайд будет выглядеть
Вставка рисунков
1. Вставьте на слайд 4 объект из Коллекции картинок.
Эскиз слайда 4 на вкладке Слайды должен быть выбран.
На слайде щелкните маленький значок Вставка картинки (с экранной подсказкой Вставка картинки).

Откроется диалоговое окно Выбор рисунка.
2. В поле Искать текст введите Горы и нажмите кнопку Начать.
Появятся эскизы рисунков, отвечающих выбранной теме.
3. В диалоговом окне отображаются эскизы гор. Их бывает трудно подобрать по цвету к шаблону оформления, однако можно отыскать изображение гор, которое будет соответствовать общему оформлению слайда. Нажмите ОК.
Выбранный рисунок будет вставлен в заполнитель для объектов, находящийся в левой части слайда, и в окне появится панель инструментов Рисунок. Рисунок на слайде останется выбранным.
4. Чтобы изменить положение рисунка с горизонтального на вертикальное, нажмите кнопку Повернуть на 90 градусов влево  на панели инструментов Рисунок.
на панели инструментов Рисунок.
5. Чтобы расширить или сузить рисунок, перетащите его маркеры выбора.
Предварительный просмотр презентации на компьютере
1. Просмотрите слайды, как если бы они демонстрировались проектором. Для этого перейдите в режим демонстрации слайдов.
В обычном режиме кнопка перехода в режим демонстрации слайдов расположена в нижней левой части окна. Это кнопка Показ слайдов  . При переходе в этот режим обычное окно PowerPoint исчезает, и чтобы вернуться к обычному режиму, необходимо либо просмотреть все слайды, либо нажать клавишу ESC.
. При переходе в этот режим обычное окно PowerPoint исчезает, и чтобы вернуться к обычному режиму, необходимо либо просмотреть все слайды, либо нажать клавишу ESC.
2. Прежде чем перейти в режим демонстрации слайдов, посмотрите, какой слайд выбран на вкладке Слайды. Если нажать кнопку Показ слайдов, когда выбран эскиз слайда 3, демонстрация начнется со слайда 3. Чтобы начать демонстрацию с первого слайда, выберите слайд 1 и нажмите кнопку Показ слайдов. Кроме того, при нажатии на клавиатуре клавиши F5 демонстрация всегда начинается со слайда 1.
Нажмите клавишу F5 и перейдите в режим демонстрации слайдов.
3. После нажатия клавиши F5, переводящего программу в режим демонстрации слайдов, переместите мышь и найдите панель инструментов Показ слайдов, которая должна появиться в нижнем левом углу окна. Она выглядит так:

4. Щелкните стрелку "Далее", чтобы перейти к следующему слайду. Переместив мышь, снова отобразите панель на экране и щелкните значки на панели, чтобы ознакомиться с соответствующими меню.
5. Чтобы просмотреть остальные слайды презентации, щелкните стрелку "Далее", щелкните мышью, нажмите клавишу PAGE DOWN или клавишу СТРЕЛКА ВНИЗ. Когда появится черный экран, щелкните его, чтобы вернуться в обычный режим. Теперь снова появляется доступ к интерактивным инструкциям.
Примечание. Если панель Показ слайдов не появляется, выполните следующие действия. В меню Сервис выберите команду Параметры, а затем щелкните вкладку Вид. Установите флажок Показывать кнопку контекстного меню.
6. Вернитесь в обычный режим. В предварительном просмотре вы имитировали просмотр слайдов и перемещение между ними. Однако имеются и другие способы настройки презентации.
7. Чтобы познакомиться с ними, в меню Показ слайдов в обычном режиме выберите команду Настройка презентации. Найдите параметры группы Показ слайдов в верхнем левом углу. Здесь выбран параметр Управляемый докладчиком (полный экран).
8. Другой вариант – Управляемый пользователем (окно). При этом презентация открывается в окне обозревателя. Для перемещения при этой настройке щелкните не сам слайд, а стрелку Следующий слайд в нижней части правой полосы прокрутки или нажмите клавишу PAGE DOWN либо клавишу со стрелкой.
9. Нажмите кнопку Отмена, чтобы закрыть диалоговое окно.
Лабораторная работа № 7
Задание 1. Знакомство с программой PhotoShop .

| Главное меню |
| Панель свойств инструмента |
| Панель инструментов |
| Палитра Naviator |
| Строка статуса |
| Палитра Swatches |
| Палитра Layer |
| Рабочее поле документа |
| Рис. 1 |
ЗАДАЧА 1 . Выбрать инструмент.
• Навести курсор мыши на пиктограмму какого-либо инструмента на панели инструментов (Рис.1), не нажимая мышь.
Рядом с пиктограммой появится название инструмента. Буква в скобках — «закреплённая» за инструментом клавиша.
• Нажать ЛКМ (левую клавишу мыши) или нажать на клавиатуре «закреплённую» клавишу.
Теперь выбранный инструмент изображён на светлом фоне.
ЗАДАЧА 2. Выбрать дополнительный инструмент.
В нижнем правом углу пиктограмм некоторых инструментов стоит маленький треугольник. Это значит, что за этим инструментом «спрятаны» дополнительные инструменты.
• Установить курсор на пиктограмму инструмента, где есть треугольник.
• Нажать ЛКМ и дождаться появления дополнительных инструментов (Можно нажать ПКМ, инструменты появятся сразу).
• Переместить курсор на пиктограмму дополнительного инструмента, не отпуская кнопки мыши.
• Отпустить кнопку мыши.
Дополнительный инструмент выбран. Кроме того, на панели инструментов появилась его пиктограмма.
Кроме панели инструментов на экране могут располагаться другие панели — вспомогательные окна, предназначенные для выполнения различных операций над изображениями. По умолчанию эти панели разделены на три группы и располагаются, как правило, вертикально вдоль правого края окна (рис. 1).
Средства группы Color /Swatches /Brushes (Синтез/Каталог/Кисти) дают возможность выбирать, создавать и редактировать цвета, а также выбирать размер и форму кончика кисти для рисования.
Группа Navigator /Info /Options (Навигатор/Инфо/Параметры) используется для изменения масштаба демонстрации изображения, а также содержит информацию о цвете пикселей и параметрах выбранного инструмента.
Группа Layers /Channels /Paths /History /Actions (Слои /Каналы /Контуры / История/Действия /) обеспечивает работу с каналами, слоями и контурами. А также содержит последовательность команд (историю) работы с изображением, средства для запоминания набора часто повторяющихся операций, которые можно многократно вызывать по имени.
В каждой группе видна только одна из панелей. Корешок активной панели помечен белым цветом (рис. 1)
. ЗАДАЧА 3 . Спрятать группу панелей, к примеру, Color /Swatches /Brushes (Синтез/Каталог/Кисти).
• Навести курсор мыши на кнопку закрытия окна. Нажать ЛКМ.
ЗАДАЧА 4 . Вывести спрятанную группу панелей на экран.
• Выполнить команду Window /Show Swatches (Окно/Показать каталог).
Аналогично с помощью команд меню Window (Окно) можно вывести на экран любую спрятанную группу панелей.
Кроме того, одним нажатием клавиши можно спрятать и показать все панели сразу.
ЗАДАЧА 5 . Спрятать все панели, а затем снова вывести их на экран.
• Нажать клавишу Tab.Панели исчезли с экрана.
• Нажать клавишу Tab снова. Панели вновь появились на экране.
У каждой панели есть своё раскрывающееся меню с дополнительными командами.
ЗАДАЧА 6 . Открыть меню панели.
• Выбрать панель, например, Swatches (Каталог).
• Навести курсор мыши на чёрный треугольник в верхнем правом углу панели. Нажать на ЛКМ.
Откроется меню с командами.
Чтобы закрыть меню команд, нужно нажать клавишу Esc.
Панели занимают довольно много места, поэтому на экране нужно размещать только самые необходимые из них. Если панель не понадобится в ближайшее время, её лучше выделить из группы и закрыть.
ЗАДАЧА 7. Выделить панель из группы панелей.
• Выбрать панель, например, Swatches (Каталог).
• Установить курсор на корешок панели.
• Нажать ЛКМ.
• Перетащить панель при нажатой кнопке на новое место. Таким образом, панель отделилась от группы панелей и её можно закрыть.
Панели можно объединять в произвольные группы.
ЗАДАЧА 8. Выделить панели из групп по умолчанию и составить свою собственную группу панелей.
Объединим в одну группу панели Brushes (Кисти) и Info (Инфо).
• Выделить панель Brushes (Кисти) из группы панелей.
• Установить курсор на корешок панели Info (Инфо).
• Нажать ЛКМ.
• Перетащить панель Info (Инфо) при нажатой кнопке на панель Brushes (Кисти).
Теперь панели Brushes (Кисти) и Info (Инфо) образуют отдельную группу.
PhotoShop позволяет вернуть все группы панелей в исходное состояние.
ЗАДАЧА 9 . Вернуть все группы панелей в исходное состояние (принятое по умолчанию).
• Выполнить команду Windows /Reset Palette Locations (Окно/Вернуть рас положение палитр).
Все панели вернулись в исходное состояние.
В PhotoShop изображения можно просматривать в разном масштабе: от 0,2% до 1600%. Для выполнения последующих заданий необходимо открыть или нарисовать самим какое-нибудь изображение.
ЗАДАЧА 10 . Увеличить изображение.
Вариант 1
• Выполнить команду View / Zoom In (Просмотр/Увеличить).
В строке заголовка документа, а также в строке состояния главного окна (слева) выводится масштаб изображения в процентах.
Вариант 2
• Выбрать инструмент Zoom (Масштаб).
• Переместить курсор на изображение.
На изображении появится лупа со знаком +.
• Нажать ЛКМ.
Вариант 3
• Выбрать панель Navigator (Навигатор).
Панель Navigator (Навигатор) состоит из окна просмотра (вверху) и строки управления масштабом (в нижней части). В окне просмотра видно всё изображение целиком. Цветная рамка отмечает часть изображения, видимую в окне документа.
• Ввести новое значение масштаба в поле ввода в левом нижнем углу палитры
или
• Переместить регулятор (в форме треугольника) по шкале вправо или
• Навести курсор мыши на кнопку увеличения масштаба (с большими треугольниками). Нажать ЛКМ.
Каждое следующее нажатие ЛКМ на этой кнопке увеличивает масштаб изображения на фиксированное значение.
ЗАДАЧА 11 . Увеличить фрагмент изображения.
Вариант 1
• Выбрать инструмент Zoom (Масштаб).
• Обвести вокруг фрагмента изображения прямоугольную рамку.
• Вариант 2
• Выбрать панель Navigator (Навигатор).
• Нажать клавишу <Ctrl>.
• Переместить курсор на изображение в окне просмотра панели. Каждый следующий щелчок на этой кнопке уменьшает масштаб изображения на фиксированное значение.
Инструмент Zoom (Масштаб) позволяет в любой момент вернуться к 100-процентному размеру изображения независимо от текущего масштаба.
ЗАДАЧА 12 . Восстановить 100-процентный размер изображения.
• Навести курсор на инструмент Zoom (Масштаб). Дважды нажать ЛКМ.
Замечание. Следует иметь в виду, что команды просмотра и инструмент Zoom (Масштаб) изменяют только экранное представление изображения, а не его фактический размер.
Для вывода на экран той части изображения, которая не умещается в окне, используется инструмент Hand (Рука).
ЗАДАЧА 13 . Переместить изображение в пределах окна.
Вариант 1
• Уменьшить размер окна так, чтобы оно стало меньше изображения.
• Выбрать инструмент Hand (Рука).
• Переместить курсор на изображение.
• Нажать кнопку мыши.
• Перемещать мышь при нажатой кнопке до тех пор, пока на экране не появится часть изображения, оказавшаяся за пределами окна.
Замечание. Когда изображение помещается в окне полностью, протягивание «рукой» не даёт никакого эффекта.
Вариант 2
• Выбрать панель Navigator (Навигатор).
• Поместить курсор во внутреннюю область рамки просмотра. Курсор примет форму руки.
• Нажать кнопку мыши.
Перемещать рамку при нажатой кнопке.
Задание 2. Работа с текстом в программе Photoshop 6
ЗАДАЧА 1. Изобразить текст, расположенный по горизонтали.
• 




| Рис. 1 |
| Горизонтальное/ вертикальное направление |
| Размер |
| Толщина |
| Цвет |
| Искривление |
• Выбрать инструмент Туре (Текст). Курсор мыши примет вид, напоминающий букву I.
• На панели свойств инструмента (Рис.1) выбрать гарнитуру шрифта MS Sans Serif (кириллические шрифты расположены внизу списка гарнитур под чертой), его размер 60 pt, цвет бордовый.
•
• Навести курсор мыши на ту части документа, где должна располагаться первая буква текста, и набрать слово русскими буквами. Окно программы должно выглядеть так, как на рис.2.

| Рис. 3 |

| Рис. 2 |
Замечание. Для ввода текста, расположенного по вертикали, необходимо воспользоваться дополнительным инструментом на панели свойств (Рис.1) Vertical Туре (Вертикальный текст).
ЗАДАЧА 2. Выполнить редактирование текста.
• Щёлкнуть на строке текстового слоя в палитре слоев. Выбрать инструмент Text (Текст)
Последние версии PhotoShop поддерживают посимвольное форматирование. Это означает, что можно изменять параметры отдельных символов текста.
•Выделить символы, для которых необходимо изменить параметры:
• 
| Рис. 4 |
• нажать ЛКМ
• переместить курсор за последний выделяемый символ, не отпуская ЛКМ.
• Изменить шрифт, размер шрифта, цвет. (Рис.4)
ЗАДАЧА 3 . Создать тень для надписи.
• Выделить текстовый слой.
• Выполнить команду Layer / Layer style / Drop Shadow (Слой / Стиль слоя /Падающая тень).
Откроется окно Layer style(Рис.).
• Установить значение параметров тени:
Mode (Режим наложения) =» Normal (Нормальный); Opacity (Непрозрачность) = 75%. Angle (Угол) = 130о;Distance (Расстояние) = 12; Spread (Четкость) = 10; Size (Размер ) = 11;. Результат — на рис. 6.

| Рис. 5 |
ЗАДАЧА 4 . Изменить параметры эффекта.

| Рис. 6 |
Снова откроется диалоговое окно Layer style (Стили слоя).
• Изменить параметры эффекта в этом окне.
• Щёлкнуть на ОК.
ЗАДАЧА 5 . Применить к слою эффект объёма.
• Выделить слой с текстом.
• Выполнить команду Layer / Layer style / Bevel and Emboss (Слой/Эф фекты / кос и рельеф).
• 
| Рис. 7 |
Поэкспериментируйте с другими значениями параметров эффекта объёма в окне Layer style (Стили слоя).
Хотя PhotoShop не является универсальным средством обработки текстов, его возможности позволяют создавать достаточно интересные текстовые эффекты.
ЗАДАЧА 6. Преобразовать текстовый слой в растровый.
Выделить текстовый слой.
• Выполнить команду Layer / Rasterize / Type (Слой / Растеризация / Тип ).
Текстовый слой преобразован в обычный. В его строке на панели Layers (Слои) исчезла буква Т.

| Рис. 8 |
• Выделить текст. Для этого навести курсор мыши на пиктограмму слоя с текстом в палитре слоев. Нажать ЛКМ при нажатой клавише <Ctrl>. Буквы текста выделятся обводкой из «бегущих муравьев».
• Выбрать инструмент Gradient (Градиент) на панели инструментов.
• Выбрать ярко-оранжевый в качестве основного цвета.
• Выбрать жёлтый в качестве фонового цвета.
• Установить курсор мыши в левом верхнем углу выделения.
• Нажать ЛКМ.
• Протянуть курсор до нижней левой границы выделения при нажатой ЛКМ.
Текст закрашен градиентом.
• Отменить выделение текста.
| Рис. 9 |
 Воспользуемся некоторыми специальными эффектами для создания тени и имитации объёма.
Воспользуемся некоторыми специальными эффектами для создания тени и имитации объёма.
ЗАДАЧА 8 . Создать перспективную тень для текста (рис. 8).
Для выполнения этого задания создадим новый документ.
• Выполнить команду File / New (Файл / Новый). Откроется окно New (Новый).
•Установить параметры документа, например,Width (Ширина) = 15 cm (см);
Height (Высота) = 10 cm (см);
Resolution (Разрешение) = 72 pixels/inch (пиксель/дюйм);
Mode (Режим) = RGB Color (Модель RGB);
Contents (Фон) = White (Белый);
• Нажать ЛКМ на ОК.
Откроется окно нового документа с именем Untitled-1.
• Ввести текст, например, слово «ТЕНЬ» со следующими параметрами:
Font (Шрифт)=МS Sans Serif;
Size (Размер) = 60 pixels;
Color (Цвет) = тёмно-синий.
• • Преобразовать текстовый слой в обычный (Выполнить команду Layer / Rasterize / Type (Слой / Растеризация / Тип )).
.Выполнить команду Layer / Duplicate Layer (Слой / Копия слоя). Откроется окно Duplicate Layer (Копия слоя).
• Сохранить установки по умолчанию для копии слоя.
В палитре слоев появился новый слой с именем &&&& copy. Этот слой является активным.
• Сдвинуть копию ниже основного текста.
• Выполнить команду Edit / Transform / Flip Vertical (Правка / Преобразование / Перевернуть до вертикали).
Теперь создадим градиентную заливку для тени.
• Выделить буквы тени.
• Выбрать инструмент Gradient (Градиент) на панели инструментов.
• Выбрать тёмно-синий в качестве основного цвета.
• Выбрать белый в качестве фонового цвета.
Дважды нажать ЛКМ на пиктограмме инструмента Gradient (Гра диент).
• Откроется панель Gradient Options (Параметры градиента).
• Выбрать на панели вариант Foreground to Background (От основного к фоновому).
• Установить курсор мыши в верхней части любой буквы тени.
• Нажать ЛКМ.
• НЕ отпуская ЛКМ, протянуть курсор до основания текста.
• Снять выделение с текста.
Добавим эффект размытия.
• Выполнить команду Filter / Blur / Gaussian Blur (Фильтр / Размы тие / Размытие по Гауссу).
Откроется окно Gaussian Blur (Размытие по Гауссу).
• Установить значение в поле Radius (Радиус) равным 1,2.Преобразуем форму тени.
• Выполнить команду Edit / Transform / Perspective (Правка / Пре образование / Перспектива).
Вокруг изображения появится рамка с ограничителями.
• Установить курсор мыши на нижний правый (или нижний левый) ограничитель.
• Нажать кнопку мыши.
• Перемещать мышь вправо (влево) при нажатой кнопке.
• Отпустить кнопку мыши, когда изображение тени примет желаемый вид.
• Дважды щёлкнуть мышью внутри рамки для завершения операции.
• Отрегулировать размер тени.
ЗАДАЧА 9 . Разместить рельефный текст по траектории (рис. 10).
• Создать новый документ.
• Ввести текст синего цвета, например, Happy new year!
Вариант 1. Выбрать инструмент Text (Текст).
| Рис. 10 |
 • Выбрать на панели свойств свойство « Create warped text » «Искривление». В раскрывшемся списке выбрать вид искривления (Рис.1).
• Выбрать на панели свойств свойство « Create warped text » «Искривление». В раскрывшемся списке выбрать вид искривления (Рис.1).
• • Выбрать тип тени и рельеф в меню Layer / Layer style / Bevel and Emboss (Слой / Стиль слоя / Скос и рельеф) в окне Layer style.
Результат виден на рис.11.
| Рис. 11 |
 Вариант 2. • Преобразовать текстовый слой в обычный.
Вариант 2. • Преобразовать текстовый слой в обычный.
Для последующего применения фильтра Distort (Деформация) текст необходимо повернуть на 90 градусов.
•
| Рис. 12 |
 Выполнить команду Edit / Transform /Rotate 90 CW (Правка / Преобразование / Поворот на 90 градусов по часовой стрелке).
Выполнить команду Edit / Transform /Rotate 90 CW (Правка / Преобразование / Поворот на 90 градусов по часовой стрелке).
• Выполнить команду Filter / Distort / Sheare (Фильтр / Деформа ция / Искривление).
Откроется окно Sheare (Искривление), в левом нижнем углу которого находится траектория, вдоль которой располагается текст.
• Изменить форму траектории. Снова перевернём текст.
• Выполнить команду Edit / Transform / Rotate 90 CCW (Прав ка / Преобразование / Поворот на 90 градусов против часовой стрелке). Результат изображен на рис 12.
•
| Рис. 13 |
 Выполнить команду Layer / Layer style / Bevel and Emboss (Слой / Стиль слоя / Скос и рельеф) (рис.13).
Выполнить команду Layer / Layer style / Bevel and Emboss (Слой / Стиль слоя / Скос и рельеф) (рис.13).
Применим к слою Background фильтр Облака, который использует основной и фоновый цвета, установленные на палитре инструментов.
§ Активизировать слой Background.
· Установить в качестве основного голубой цвет.
· Установить в качестве фонового белый цвет.
· Выполнить команду Filter / Render / Clouds (Фильтр / Освещение / Облака).
Воспользуемся фильтром Океанская рябь, поскольку он может подчеркнуть в изображении «ощущение» льда.
| Рис. 14 |
 • Выполнить команду Filter / Distort / Ocean Ripple (Фильтр / Иска жение / Океанская рябь).
• Выполнить команду Filter / Distort / Ocean Ripple (Фильтр / Иска жение / Океанская рябь).
Откроется диалоговое окно Ocean Ripple (Океанская рябь).
• Подобрать значения параметров для этого фильтра.
Московский Городской Педагогический Университет
[1] Факультет
Кафедра [2]
[3] работа
На тему
«[4]».
Выполнил[5]:
студент[6] [7] курса группы [8] [9] отделения [10]
Научный руководитель: [11]
Москва 20[17]г.
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ДИЗАЙНА И ТЕХНОЛОГИЙ
ПРОЕКТ
Введение
Перед тем, как нам перейти к методике разработки экспертной (информационной) системы, необходимо сказать несколько слов о компьютерном контент-анализе текстовой информации (ККАТИ).
Компьютерный к онтент-анализ – количественный анализа текстов и текстовых массивов с целью последующей содержательной интерпретации выявленных числовых закономерностей. Основная идея контент-анализа проста и интуитивно наглядна.
При восприятии текста и особенно больших текстовых потоков мы достаточно хорошо ощущаем, что разные формальные и содержательные компоненты представлены в них в разной степени, причем эта степень по крайней мере отчасти поддается измерению: ее мерой служит то место, которое они занимают в общем объеме, и/или частота их встречаемости.
Замысел компьютерного контент-анализа заключается в том, чтобы систематизировать интуитивные ощущения, а также сделать их наглядными и проверяемыми и разработать методику целенаправленного сбора тех текстовых свидетельств, на которых эти ощущения основываются. При этом предполагается, что вооруженный такой методикой исследователь сможет не просто упорядочить свои ощущения и сделать свои выводы более обоснованными, но даже узнать из текста больше, чем хотел сказать его автор. Скажем, настойчивое повторение в тексте каких-то тем или употребление каких-то характерных формальных элементов или конструкций может не осознаваться автором, но обнаруживает и определенным образом интерпретируется исследователем - отсюда принадлежащее социологу А.Г. Здравомыслову его полушутливое определение контент-анализа как «научно обоснованного метода чтения между строк».
Реально главной отличительной чертой контент-анализа является не его декларируемая во многих определениях «систематичность» и «объективность» (эти черты присущи и другим методам анализа текстов), а его квантитативный (количественный) характер. Компьютерныйк онтент-анализ (ККАТИ) – это прежде всего количественный метод, предполагающий числовую оценку каких-то компонентов текста, дополняющийся также различными качественными классификациями и выявлением тех или иных структурных закономерностей.
Поэтому наиболее удачным определением для такого контент-анализа можно считать то, которое зафиксировано в относительно недавней книге Мангейма и Рича: контент-анализ – это систематическая числовая обработка, оценка и интерпретация формы и содержания информационного источника.
В качестве примера приведем стихотворение Ф.И. Тютчева «Рим ночью» (Текст 1):
В ночи лазурной почивает Рим.
Взошла луна и овладела им,
И спящий град, безлюдно-величавый,
Наполнила своей безмолвной славой...
Как сладко дремлет Рим в ее лучах!
Как с ней сроднился Рима вечный прах!..
Как будто лунный мир и град почивший —
Всё тот же мир, волшебный, но отживший!..
<1850>
Нашей задачей является построение экспертной (Информационной) системы для оценки поэтических текстов Ф.И. Тютчева.
| № |
Название
Автор
1
«Рим ночью»
Ф.И. Тютчев
2
«Русской женщине»
Ф.И. Тютчев
3
«Успокоение»
Ф.И. Тютчев
Для этих текстов вычислены следующие показатели: Н1, Н2, ∆ , S и λ1, λ2, λ3.
|
Выводы по проекту Учебно-методический комплекс Дисциплины (УМКД) |
|||||||||
Последнее изменение этой страницы: 2019-04-19; Просмотров: 364; Нарушение авторского права страницы