
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Який вигляд має максвеллівський розподіл швидкостей молекул і що він показує ?
Одним з положень молекулярно-кінетичної теорії є припущення, що молекули, з яких складається газ, рухаються хаотично і місцезнаходження будь-якої молекули має випадковий характер. Окрім цього молекули нічим не відрізняються одна від одної і їх дуже багато (наприклад в 1см Для визначення і розрахунку середніх величин, що характеризують великий ансамбль одиниць, для яких наведені положення задовольнюються, використовуються методи статистичних досліджень, тобто науки статистики. Статистика оперує такими величинами, як імовірність, флуктуація, функція статистичного розподілу, середні значення, то саме такими величинами і можна буде характеризувати газ. Будемо вважати, що всі напрями в газі рівноймовірні і тому молекули можуть мати швидкість v, що не залежить від напряму. Взаємодіють молекули тільки в результаті пружних зіткнень, а тому матимуть найрізніші швидкості як за напрямом, так і за величиною. Наше завдання полягає в тому, щоб знайти закон, за яким будуть розподілятися швидкості молекул газа. Позначимо в декартовій системі координат число молекул, швидкості яких в напрямі осі x лежать в межах від Якщо введемо результуючу швидкість як Єдиним рішенням цього рівняння буде функція Стала величина а є додатною, оскільки імовірність не може бути від’ємною. Тоді можна записати Будемо вважати, що при відповідних умовах в газі є загальна кількість молекул N. Тоді частина молекул від N, які мають швидкості в межах від
і в просторі швидкостей в декартових координатах це можна показати, як на рис. 2.2 , де певна частина молекул буде знаходитися у середині вказаного куба.
 Оскільки всі напрями швидкостей рівноймовірні, то будуть ще молекули з таким ж швидкостями за величиною, але направлені за всіма напрямами. Щоб визначити загальне число молекул з такими швидкостями, необхідно підрахувати скільки молекул буде в кульовому шарі радіусом Оскільки всі напрями швидкостей рівноймовірні, то будуть ще молекули з таким ж швидкостями за величиною, але направлені за всіма напрямами. Щоб визначити загальне число молекул з такими швидкостями, необхідно підрахувати скільки молекул буде в кульовому шарі радіусом  і товщиною і товщиною 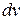 . Відомо, що об’єм такого шару дорівнює . Відомо, що об’єм такого шару дорівнює 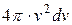 , тоді можна записати, що частина молекул , тоді можна записати, що частина молекул 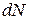 зі швидкостями від зі швидкостями від  до до  + + 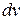 дорівнюватиме дорівнюватиме а загальне число всіх молекул N з допущенням, що вони мають швидкості від Загальне число молекул газа можна визначити незалежно від цього, тоді з рівняння (2.12) знайдемо сталі а і b. Дійсно, інтеграл в (2.12) буде скінченним тільки за умови, що значення сталої b є від’ємним. Таким чином b<0. Окрім цього, показник експоненти повинен бути безрозмірним, а тому розмірність b має бути оберненою до Після проведення інтегрування в (2.12) при врахуванні, що а також, що після диференціювання інтеграла в (2.13) за параметром отримаємо 1= і визначимо сталу , тобто Підставляючи визначені сталі в (2.11), отримаємо Це рівняння називають максвелловським розподілом швидкостей газу у відповідному стані за визначеними значеннями u і N. |
Последнее изменение этой страницы: 2019-04-19; Просмотров: 166; Нарушение авторского права страницы