
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Линейные операции над векторами.Стр 1 из 3Следующая ⇒
Транспонирование матриц Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка. Свойства транспонированной матрицы: 1. (AT)T=A 2. Линейность: (A+B)T = AT+BT 3. Умножение на число: (xA)T = x*(AT) 4. (A*B)T = BT*AT Умножение матриц
Свойства умножения 1. АB != BA 2. 0A = A0 = 0 3. ABC = A(BC) 4. (A+B)C = AC + BC Пример 1. Рассмотрим для начала простейший пример, когда необходимо найти произведение двух матриц А и В размером 2x2, если
Решение:
Элементы матрицы С находятся по следующему алгоритму: Элемент матрицы С, стоящий на первой строке, в первом столбце находится как сумма произведений первой строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на первой строке, во втором столбце находится как сумма произведений первой строки матрицы А на второй столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, в первом столбце находится как сумма произведений второй строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, во втором столбце находится как сумма произведений второй строки матрицы А на второй столбец матрицы В.
Таким образом, мы получили
То есть мы получили, что
№8. Определители n-го порядка. Их свойства и методы вычисления. Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца. Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей : если оно четное «+», нечетное «-». Инверсия - когда большее число стоит перед меньшим. Св-ва определителей: 1. В определителе строки и столбцы равнозначны. 2. Если все Эл-ты в строке или столбце = 0, то определитель =0. 3. Общий множитель строки или столбца можно выносить. 4. Если в определителе переставить местами 2 строки, то знак определителя изменится на противоположный. 5. Если в определителе 2 одинаковых строки/столбца, то определитель =0. 6. Если в определителе 2 строки пропорциональны, то определитель =0. 7. Определитель можно разложить на сумму. 8. Если в определителе некоторая строка/столбец является линейной комбинацией другой строки-столбца, то определитель =0. 9. Если к Эл-ам некоторой строки добавить соотв. Эл-ты другой строки умноженные на число не равное 0, то определитель не изменится. Минор- определитель полученный из определителя n-го порядка вычеркиванием К каких-то строк и К столбцов. Теорема Лапласа. Определитель n-го порядка равен сумме произведений Эл-ов некоторой строки/столбца на их алгебраические дополнения. Алгебраическое дополнение – Aij=(-1)i+jMij Определитель треугольного вида равен произведению Эл-ов главной диагонали. №9. Обратная матрица. Ее свойства и методы вычисления. Определение: А-1 называется обратной матрице А, если выполняются условия A·A-1= A-1·A=E Теорема: если для матрицы А существует обратная, то она единственная. Теорема: для того, чтобы для квадратной матрицы А существовала A-1 необходимо и достаточно, чтобы определитель Первый способ нахождения ОМ: 1) Находим алгебраические дополнения (АД) для матрицы (aij - Aij). АД: например, А21 – минор, получаемый вычеркиванием 2й строки и 1го столбца 2) Составляем матрицу С = (Aij)T. 3) Второй способ: 1) Записываем матрицу (А | E). 2) Приводим левую половину к виду единичной матрицы (Е). Матрица, получившаяся справа будет обратной Для приведения матрицы к виду единичной используются следующие элементарные преобразования: 1. Перемена местами двух любых уравнений; 2. Умножение обеих частей любого из уравнений на произвольное число, отличное от нуля; 3. Прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число. Свойства ОМ: 1) (A-1) -1 = А 2) (А·B) -1 = B-1·A-1 №10. Ранг матрицы. Методы его вычисления. Ответ: Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Ранг невырожденной квадратной матрицы порядка равен, так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля. Рассмотрим прямоугольную матрицу. Выделим в этой матрице k произвольных строк и k произвольных столбцов (k≤n, k≤m). Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка. Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю. Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы. Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой равны нулю; - умножения строки на число, отличное от нуля; - прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число. Сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится. №11. Метод Гаусса для преобразования матрицы. Его применение для решения задач линейной алгебры. Метод Гаусса применим для систем т линейных уравнений с п неизвестными:
, где x1 , x2, …, xn – неизвестные. ai j - коэффициенты при неизвестных. bi - свободные члены (или правые части) Решения СЛАУ по методу Гаусса состоит из двух этапов. – Первый этап (прямой ход метода) – система приводится к треугольному виду. – Второй этап (обратный ход) – неизвестные определяются последовательно, начиная с последнего неизвестного (в последнем уравнении) и кончая первым (в первом уравнении). Для приведения матрицы к треугольному виду используются следующие элементарные преобразования: 1. перемена местами двух любых уравнений; 2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля; 3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число. После данных преобразований должна получиться треугольная матрица вида:
Для первой системы просто последовательно находят значения неизвестных, начиная с нижнего уравнения. Вторая система будет иметь бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными х k+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находят х1, … , xk, которые будут выражаться через свободные неизвестные. №12. Предел функции в точке и на бесконечности. Геометрическая интерпретация. Определенности и неопределенности, возникающие при нахождении приделов. Понятие непрерывности функции непосредственно связано с понятием предела функции. Число A называется пределом функции f в точке a, предельной для множества E, если для любой окрестности V(A) точки A, существует такая проколотая окрестность Предел функции f в точке a, предельной для множества E, обозначается так: Поскольку каждой окрестности может быть сопоставлена своя правильная (симметричная) окрестность, то определение предела можно сформулировать на языке
Предел функции в точке f в точке a, предельной для множества E, непосредственно связан с пределом последовательности. Будем рассматривать всевозможные последовательности Верно и обратное: если все последовательности Другими словами:
Пределы на бесконечности Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине). Определения, аналогичные «ε−δ» Пусть задана числовая функция с неограниченной сверху областью определения, то есть
Пишут:
Аналогично пусть
Пишут:
Если пределы в Число
Неопределенность Неопределенности такого вида возникают при вычислении пределов типа: При этом возможны частные случаи: 1)Числитель Для вычисления предела необходимо разложить числитель и знаменатель на множители и сократить дробь на множитель, порождающий нуль. 2) Числитель или знаменатель дроби, или оба содержат иррациональность. Для решения примера необходимо освободиться от иррациональности, умножив числитель и знаменатель дроби на сопряженное выражение, сократить дробь на множитель, порождающий нуль. 3) Выражение содержит тригонометрические функции. Для решения примера необходимо путем тригонометрических и алгебраических преобразований свести его к первому замечательному пределу. Неопределенность вида 1) Числитель и знаменатель дроби при Для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень с наивысшим показателем, а затем перейти к пределу. Неопределенность вида Для раскрытия этой неопределенности необходимо путем преобразования исходного выражения получить неопределенность вида Неопределенность вида Этот случай нахождения предела функции можно привести к случаю
Неопределенность вида Неопределенности такого вида появляются при решении примеров вида:
Преобразуя выражения, сводим их ко второму замечательному пределу. №13. Методы нахождения предела функции в точке и на бесконечности. Замечательные пределы. 1. Подстановка: при х®х0 и х0Îобласти определения ф-ции f(x), предел ф-ции f(x)= его частному значению при х=х0 limf(x)=f(x0) x®x0 2. Сокращение: при х®¥ и х®х0 f(x)/g(x)=0/0, то сокращают числитель и знаменатель на множитель, стремящийся к 0. 3. уничтожение иррациональности (* числитель и знаменатель на 1 число). 4.деление на наивысшую степень х: при х®¥ и х®х0 f(x)/g(x)=0/0, то делим числитель и знаменатель на наивысшую степень. 5. Приведение к замечательным пределам: Сравнение функций
Локально эквивалентные функции:
Некоторые эквивалентности (при
Производная функции в точке Пусть дана
Если этот предел существует, то он называется производной функции f в точке
Производная функции – предел отн6ошений приращения функции к приращению аргумента, при приращении аргумента Операция вычисления или нахождения производной в точке называется дифференцированием. Метод Гаусса Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Формулы Крамера Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А Δ = det (aij) и n вспомогательных определителей Δi (i = Формулы Крамера имеют вид: Δ · xi = Δi (i = Из (1) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: xi = Δi / Δ. Если главный определитель системы Δ и все вспомогательные определители Δi = 0 (i = Матричный метод Если матрица А системы линейных уравнений невырожденная, т.е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X = C, C = A-1B называют матричным способом решения системы, или решением по методу обратной матрицы. №27. Представление чисел в памяти ЭВМ. Приближенные числа. Погрешность решения вычислительных задач, ее источники. Существуют два способа представления чисел в памяти ЭВМ. Они называются так: форма с фиксированной точкой и форма с плавающей точкой. Форма с фиксированной точкой применяется к целым числам, форма с плавающей точкой — к вещественным числам (целым и дробным). Под точкой здесь подразумевается знак-разделитель целой и дробной части числа. Приближенным числом а называется число, незначительно отличающееся от точного числа А и заменяющее его в вычислениях. Абсолютной погрешностью или, короче, погрешностью приближенного числа называется разность между этим числом и его точным значением Δx = |x – x0|. Относительной погрешностью приближённого числа называется отношение абсолютной погрешности приближённого числа к самому этому числу e(x)= Δx/ x0 Погрешность решения задачи обуславливается следующими причинами (источниками): 1. Математическое описание задачи является неточным, в частности, неточно заданы исходные данные описания.2. Применяемый для решения метод часто не является точным: получение точного решения задачи требует неограниченного или неприемлемо большого числа арифметических операций, и поэтому вместо получения точного решения приходится прибегать к приближенному.3. При выполнении арифметических операций на ЭВМ или любым другим образом, как правило, производятся округления. (Это же относится к вводу чисел в память ЭВМ и выводу полученных результатов.) Погрешности, соответствующие этим причинам, называются: неустранимая погрешность, погрешность метода, вычислительная погрешность. №28. Прямые вычислительные методы решения систем линейных алгебраических уравнений. Метод оптимального исключения. ыва №29. Итерационные вычислительные методы решения систем линейных алгебраических уравнений. Метод простой итерации. Рассмотрим систему:
Для неё итерационное вычисление буде т выглядеть так:
Сходимость методу будет осуществлять
Алгоритм: 1. Условие 2. Задаётся начальное приближение и точность 3. Вычисляется очередная итерация - Если - Иначе №30. Итерационные вычислительные методы решения не линейных уравнений. Метод бисекции. Метод простой итерации. Методы решения нелинейных уравнений (метод простой итерации, метод Ньютона, модифицированный метод Ньютона, метод секущих). Метод бисекции или метод деления отрезка пополам — простейший численный метод для решения нелинейных уравнений вида f(x)=0. Предполагается только непрерывность функции f(x). Теорема (Больцано — Коши).Пусть функция Следствие.Пусть функция
Таким образом, если мы ищем ноль, то на концах отрезка функция должна быть разных знаков. Разделим отрезок пополам и возьмём ту из половинок, для которой на концах функция по-прежнему принимает значения разных знаков. Если серединная точка оказалось искомым нулём, то процесс завершается.Если задана точность вычисления  , то процедуру следует продолжать до тех пор, пока длина отрезка не станет меньше , то процедуру следует продолжать до тех пор, пока длина отрезка не станет меньше  .Для поиска произвольного значения достаточно вычесть из значения функции искомое значение и искать ноль получившейся функции. Задача заключается в нахождении корней нелинейного уравнения .Для поиска произвольного значения достаточно вычесть из значения функции искомое значение и искать ноль получившейся функции. Задача заключается в нахождении корней нелинейного уравнения  Для начала итераций необходимо знать интервал [xL,xR] значений x, на концах которого функция принимает значения разных знаков: Для начала итераций необходимо знать интервал [xL,xR] значений x, на концах которого функция принимает значения разных знаков:  Из непрерывности функции f и условия (2) следует, что на интервале [xL,xR] существует хотя бы один корень уравнения (в случае наличия нескольких корней метод приводит к нахождению одного из них)Выберем точку внутри интервала Из непрерывности функции f и условия (2) следует, что на интервале [xL,xR] существует хотя бы один корень уравнения (в случае наличия нескольких корней метод приводит к нахождению одного из них)Выберем точку внутри интервала  Если f(xM) = 0, то корень найден. Если Если f(xM) = 0, то корень найден. Если 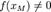 разобьём этот интервал на два [xL,xM] и [xM,xR]. Теперь найдём новый интервал, в котором функция меняет знак. Пусть разобьём этот интервал на два [xL,xM] и [xM,xR]. Теперь найдём новый интервал, в котором функция меняет знак. Пусть  и соответственно корень находится внутри интервала [xL,xM]. Тогда обозначим xR=xM и повторим описанную процедуру до достижения требуемой точности. За количество итераций N первоначальный отрезок делится в 2N раз. Метод простой итерации (метод последовательных повторений). Для применения метода простой итерации следует исходное уравнение и соответственно корень находится внутри интервала [xL,xM]. Тогда обозначим xR=xM и повторим описанную процедуру до достижения требуемой точности. За количество итераций N первоначальный отрезок делится в 2N раз. Метод простой итерации (метод последовательных повторений). Для применения метода простой итерации следует исходное уравнение  преобразовать к виду, удобному для итерации преобразовать к виду, удобному для итерации  . Это преобразование можно выполнить различными способами. Функция . Это преобразование можно выполнить различными способами. Функция 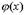 называется итерационной функцией. Расчетная формула метода простой итерации имеет вид: называется итерационной функцией. Расчетная формула метода простой итерации имеет вид:  . Теорема о сходимости метода простой итерации. Пусть в некоторой . Теорема о сходимости метода простой итерации. Пусть в некоторой  - окрестности корня - окрестности корня  функция функция 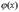 дифференцируема и удовлетворяет неравенству дифференцируема и удовлетворяет неравенству  , где , где  - постоянная . Тогда независимо от выбора начального приближения из указанной - постоянная . Тогда независимо от выбора начального приближения из указанной  - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится cо скоростью геометрической последовательности и справедлива оценка погрешности: - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится cо скоростью геометрической последовательности и справедлива оценка погрешности: 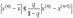 , ,  .Критерий окончания итерационного процесса. При заданной точности .Критерий окончания итерационного процесса. При заданной точности  >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство  . Если величина . Если величина  , то можно использовать более простой критерий окончания итераций: , то можно использовать более простой критерий окончания итераций:  .Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду .Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду  . Предположим дополнительно, что производная . Предположим дополнительно, что производная  знакопостояна и знакопостояна и  на отрезке [a,b]. Тогда при выборе итерационного параметра на отрезке [a,b]. Тогда при выборе итерационного параметра 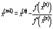 метод ходится и значение метод ходится и значение  . .
Линейные операции над векторами. В математике различают скалярные и векторные величины. Скалярные величины полностью определяются своим значением, например, температура тела, масса, объем и т.д. Но для силы, скорости, ускорения, кроме величины надо указать еще и направление в пространстве. Такие величины называют векторными. Отметим также, что с математической точки зрения вектором можно назвать любой объект, а не только направленный отрезок. Лишь бы были определены операции их сложения и умножения на число. Вектором называется направленный отрезок AB с начальной точкой A и конечной точкой B, обозначается AB. Будем считать, что два вектора AB и CD равны, если они одинаково направлены и длины отрезков AB и CD равны |CD|=|AB|. Cвободные векторы это такие векторы, которые можно перемещать параллельно самим себе. Нулевым называется вектор, начало, и конец которого совпадают. Длина нулевого вектора равна нулю, и ему можно принимать любое направление. Длиной или нормой вектора AB называется длина отрезка AB и обозначается |AB|. Вектор a, длина которого равна 1, называется единичным или ортом. Векторы, параллельные одной прямой, называются коллинеарными. Векторы, параллельные одной плоскости, называются компланарными. Суммой двух векторов a и b называется вектор b+a. Суммой конечного числа n векторов a1,a2,…,an называется замыкающий вектор O A n. Вектор (-b) называется противоположным вектору b, если (−b)||b,||- b||=||b|| и его направление противоположно вектору b. Разностью двух векторов a и b называется вектор a−b, являющийся суммой векторов a и (-b ). Произведением вектора a на действительное число α называется вектор b=aα, длина которого |b|=|aα|=|a||α|, а направление совпадает с a, если 0<λ и противоположно a, если 0>α. Введенные операции сложения векторов и умножения на число называются линейными и обладают свойствами коммутативности, ассоциативности и дистрибутивности: №2. Линейная зависимость и линейная независимость векторов. Базис. Представление векторов в базисе Линейной комбинацией называется множество векторов вида:
Теорема: векторное множество будет линейно-независимым, если линейная комбинация этих векторов обращается 0, когда действительные множители равны 0 (ни один из векторов не выражается через другие).
Любые 4 вектора в пространстве линейно независимы. Базисом на прямой называется любой ненулевой вектор на этой прямой. Базисом на плоскости называются любые 2 линейно независимых вектора, взятые в определенном порядке. Базисом в пространстве называются любые 3 линейно независимых вектора, взятые в определенном порядке. Выражение Основное значение базиса заключается в том, что вместо выполнения линейных операций над векторами можно выполнять операции над их координатами. №3. Скалярное произведение двух векторов, его свойства. Вычисление в декартовой системе координат. Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Свойства: 1. Переместительное: ab=ba 2. Ассоциативность: 3. Дистрибутивность: 4. 5. Вычисление: a*b = x1x2 + y1y2 + z1z2 №4. Векторное произведение двух векторов, его свойства, Вычисление в декартовой системе координат. Геометрический смысл. Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям: длина вектора c равна произведению длин векторов a и b на синус угла φ; между ними Геометрически векторное произведение Свойства векторного произведения:1)При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е №5. Смешанное произведение трех векторов, его свойства. Вычисление в декартовой системе координат. Геометрический смысл. Смешанным произведенем трех векторов a, b, c называется число, равное векторному произведению (a*b), множенному скалярно на вектор c, то есть (a*b)c. Свойства: 1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с х а)•b . 2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb )•с=а*(bx с). 3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba . 4. Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны. Если abc =0 , то а, b и с— компланарны. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. №6. Матрица. Их виды. Линейные операции над матрицами. Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Квадратной называют матрицу, количество строк в которой равно количеству столбцов. Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Диагональная матрица — квадратная матрица, все недиагональные элементы которой равны нулю. Обра́тная ма́трица — такая матрица A-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E: №7. Умножение матриц. Транспонирование матриц. Транспонирование матриц Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка. Свойства транспонированной матрицы: 1. (AT)T=A 2. Линейность: (A+B)T = AT+BT 3. Умножение на число: (xA)T = x*(AT) 4. (A*B)T = BT*AT Умножение матриц
Свойства умножения 1. АB != BA 2. 0A = A0 = 0 3. ABC = A(BC) 4. (A+B)C = AC + BC Пример 1. Рассмотрим для начала простейший пример, когда необходимо найти произведение двух матриц А и В размером 2x2, если
Решение:
Элементы матрицы С находятся по следующему алгоритму: Элемент матрицы С, стоящий на первой строке, в первом столбце находится как сумма произведений первой строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на первой строке, во втором столбце находится как сумма произведений первой строки матрицы А на второй столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, в первом столбце находится как сумма произведений второй строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, во втором столбце находится как сумма произведений второй строки матрицы А на второй столбец матрицы В.
Таким образом, мы получили
То есть мы получили, что
№8. Определители n-го порядка. Их свойства и методы вычисления. Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца. Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей : если оно четное «+», нечетное «-». Инверсия - когда большее число стоит перед меньшим. Св-ва определителей: 1. В определителе строки и столбцы равнозначны. 2. Если все Эл-ты в строке или столбце = 0, то определитель =0. 3. Общий множитель строки или столбца можно выносить. 4. Если в определителе переставить местами 2 строки, то знак определителя изменится на противоположный. 5. Если в определителе 2 одинаковых строки/столбца, то определитель =0. 6. Если в определителе 2 строки пропорциональны, то определитель =0. 7. Определитель можно разложить на сумму. 8. Если в определителе некоторая строка/столбец является линейной комбинацией другой строки-столбца, то определитель =0. 9. Если к Эл-ам некоторой строки добавить соотв. Эл-ты другой строки умноженные на число не равное 0, то определитель не изменится. Минор- определитель полученный из определителя n-го порядка вычеркиванием К каких-то строк и К столбцов. Теорема Лапласа. Определитель n-го порядка равен сумме произведений Эл-ов некоторой строки/столбца на их алгебраические дополнения. Алгебраическое дополнение – Aij=(-1)i+jMij Определитель треугольного вида равен произведению Эл-ов главной диагонали. №9. Обратная матрица. Ее свойства и методы вычисления. Определение: А-1 называется обратной матрице А, если выполняются условия A·A-1= A-1·A=E Теорема: если для матрицы А существует обратная, то она единственная. Теорема: для того, чтобы для квадратной матрицы А существовала A-1 необходимо и достаточно, чтобы определитель Первый способ нахождения ОМ: 1) Находим алгебраические дополнения (АД) для матрицы (aij - Aij). АД: например, А21 – минор, получаемый вычеркиванием 2й строки и 1го столбца 2) Составляем матрицу С = (Aij)T. 3) Второй способ: 1) Записываем матрицу (А | E). 2) Приводим левую половину к виду единичной матрицы (Е). Матрица, получившаяся справа будет обратной Для приведения матрицы к виду единичной используются следующие элементарные преобразования: 1. Перемена местами двух любых уравнений; 2. Умножение обеих частей любого из уравнений на произвольное число, отличное от нуля; 3. Прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число. Свойства ОМ: 1) (A-1) -1 = А 2) (А·B) -1 = B-1·A-1 №10. Ранг матрицы. Методы его вычисления. Ответ: Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Ранг невырожденной квадратной матрицы порядка равен, так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля. Рассмотрим прямоугольную матрицу. Выделим в этой матрице k произвольных строк и k произвольных столбцов (k≤n, k≤m). Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка. Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю. Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы. Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой равны нулю; - умножения строки на число, отличное от нуля; - прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число. Сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится. №11. Метод Гаусса для преобразования матрицы. Его применение для решения задач линейной алгебры. Метод Гаусса применим для систем т линейных уравнений с п неизвестными:
, где x1 , x2, …, xn – неизвестные. ai j - коэффициенты при неизвестных. bi - свободные члены (или правые части) Решения СЛАУ по методу Гаусса состоит из двух этапов. – Первый этап (прямой ход метода) – система приводится к треугольному виду. – Второй этап (обратный ход) – неизвестные определяются последовательно, начиная с последнего неизвестного (в последнем уравнении) и кончая первым (в первом уравнении). Для приведения матрицы к треугольному виду используются следующие элементарные преобразования: 1. перемена местами двух любых уравнений; 2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля; 3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число. После данных преобразований должна получиться треугольная матрица вида:
Для первой системы просто последовательно находят значения неизвестных, начиная с нижнего уравнения. Вторая система будет иметь бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными х k+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находят х1, … , xk, которые будут выражаться через свободные неизвестные. №12. Предел функции в точке и на бесконечности. Геометрическая интерпретация. Определенности и неопределенности, возникающие при нахождении приделов. Понятие непрерывности функции непосредственно связано с понятием предела функции. Число A называется пределом функции f в точке a, предельной для множества E, если для любой окрестности V(A) точки A, существует такая проколотая окрестность Предел функции f в точке a, предельной для множества E, обозначается так: Поскольку каждой окрестности может быть сопоставлена своя правильная (симметричная) окрестность, то определение предела можно сформулировать на языке
Предел функции в точке f в точке a, предельной для множества E, непосредственно связан с пределом последовательности. Будем рассматривать всевозможные последовательности Верно и обратное: если все последовательности Другими словами:
Пределы на бесконечности Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине). Определения, аналогичные «ε−δ» Пусть задана числовая функция с неограниченной сверху областью определения, то есть
Пишут:
Аналогично пусть
Пишут:
Если пределы в Число
Неопределенность Неопределенности такого вида возникают при вычислении пределов типа: При этом возможны частные случаи: 1)Числитель Для вычисления предела необходимо разложить числитель и знаменатель на множители и сократить дробь на множитель, порождающий нуль. 2) Числитель или знаменатель дроби, или оба содержат иррациональность. Для решения примера необходимо освободиться от иррациональности, умножив числитель и знаменатель дроби на сопряженное выражение, сократить дробь на множитель, порождающий нуль. 3) Выражение содержит тригонометрические функции. Для решения примера необходимо путем тригонометрических и алгебраических преобразований свести его к первому замечательному пределу. Неопределенность вида 1) Числитель и знаменатель дроби при Для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень с наивысшим показателем, а затем перейти к пределу. Неопределенность вида Для раскрытия этой неопределенности необходимо путем преобразования исходного выражения получить неопределенность вида Неопределенность вида Этот случай нахождения предела функции можно привести к случаю
Неопределенность вида Неопределенности такого вида появляются при решении примеров вида:
Преобразуя выражения, сводим их ко второму замечательному пределу. №13. Методы нахождения предела функции в точке и на бесконечности. Замечательные пределы. 1. Подстановка: при х®х0 и х0Îобласти определения ф-ции f(x), предел ф-ции f(x)= его частному значению при х=х0 limf(x)=f(x0) x®x0 2. Сокращение: при х®¥ и х®х0 f(x)/g(x)=0/0, то сокращают числитель и знаменатель на множитель, стремящийся к 0. 3. уничтожение иррациональности (* числитель и знаменатель на 1 число). 4.деление на наивысшую степень х: при х®¥ и х®х0 f(x)/g(x)=0/0, то делим числитель и знаменатель на наивысшую степень. 5. Приведение к замечательным пределам: |
Последнее изменение этой страницы: 2019-04-19; Просмотров: 219; Нарушение авторского права страницы