Механический смысл производной.

Пусть материальная точка движется прямолинейно вдоль прямой, тогда Найдем среднюю скорость

№18. Основные методы нахождения производной функции.

Производной функции f ( x ) в точке х=х₀ называется отношение приращения функции в этой точке к приращению аргумента, при стремлении последнего к нулю.Нахождение производной называется дифференцированием. Вычисление производной функции производится по общему правилу дифференцирования: Обозначим f ( x ) = u , g ( x ) = v- функции, дифференцируемые в точке х. Основные правила дифференцирования 1) (производная суммы равна сумме производных) 2) 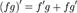(отсюда, в частности, следует, что производная произведения функции и константы равна произведению производной этой функции на константу) 3) Производная частного: , если g  0 4) Производная сложной функции: 5) Если функция задана параметрически: , то Отношение называется логарифмической производной функции f(x). Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле 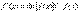Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким. Дифференцирование функций заданных параметрически До сих пор функция записывалась в явном виде y= f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в па раметрической форме в виде двух уравнений где t- вспомогательная переменная, называемая параметром. Заметим, что функция может быть представлена в параметрической форме различными способами. Например, функция, записанная в неявном виде x² + y² = 1 может быть представлена в явном виде: и в параметрической форм Заметим, что x² + y² = 1 есть уравнение окружности единичного радиуса с центром в начале координат. Если функция задана в явном виде y=f(x), то всегда можно записать её в неявном виде y-f(x)=0, а также в параметрической форме Параметрические уравнения и уравнение F(x, y)=0 представляют одну и ту же функцию, если F(x(t), y(t))=0.Продифференцируем y как сложную функцию от x, т.е. 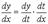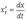по формуле и применим формулу, связывающую производные обратных функций: Введя обозначения , получим