Решение иррациональных уравнений и неравенств Стр 1 из 3Следующая ⇒ Решение иррациональных уравнений и неравенств методические рекомендации для учащихся Составитель Преподаватель математики Мочалова Е.В. Составители: Мочалова Е.В. – преподаватель математики     От авторов-составителей: Одной из нелегких и трудно усваиваемых тем на уроках математики являются иррациональные уравнения и неравенства. В работе рассмотрены основные понятия и формулы, которые нужно знать для успешного решения иррациональных уравнений и неравенств. Приведены подробные примеры решения некоторых уравнений и неравенств. Подобраны задания для самостоятельного решения и тест для проверки усвоения теоретических основ. Методические рекомендации призваны помочь при самостоятельном изучении и повторении данной темы. Причина появления посторонних корней. Решение иррациональных уравнений основано на следующем утверждении: Теорема. Если n>0 - нечетное число (n=2k+1), то уравнения fn ( x )= gn ( x ) и f ( x )= g ( x ) равносильны. Если n>0 - четное число (n=2k), то любой корень уравнения fn ( x )= gn ( x ) удовлетворяет хотя бы одному из уравнений: f ( x )= g ( x ) и f ( x )=- g ( x ). Из теоремы следует, что если в ходе решения иррационального уравнения приходилось возводить обе части в степень с четным показателем, то могут появиться "посторонние" корни уравнения. Итак, что же происходит, каковы причины посторонних корней: а) за счет возможного расширения ОДЗ исходного уравнения (т.е. ОДЗ полученного уравнения шире ОДЗ исходного уравнения). б) за счет возведения в четную степень его левой и правой частей, которые равны по абсолютной величине, но одна из них положительна, а другая отрицательна.   Решение иррациональных уравнений путем замены уравнения его следствием. Решение иррациональных уравнений путем замены уравнения его следствием (с последующей проверкой корней) можно производить следующим образом: 1. Найти ОДЗ исходного уравнения. 2. Перейти от уравнения к его следствию. 3. Найти корни полученного уравнения. 4. Проверить, являются ли найденные корни корнями исходного уравнения.   Проверка корней. Проверка корней подстановкой найденного значения в исходное уравнение сама по себе может оказать сложной задачей. Однако, чтобы отделить посторонние корни, не всегда необходимо подставлять найденные корни в данное уравнение. Иногда возможна проверка корней по ОДЗ уравнения. При решении иррациональных уравнений удобно и полезно следующие утверждения:   Уравнение вида Равносильно	Системе / совокупности систем уравнений
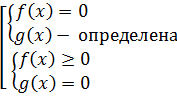
	Одной из равносильных систем:   или Выбирается та система, в которой проще неравенство.

 

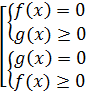
Пример 3.

<=>

 

   Ответ: 3.

b) 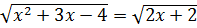 <=>  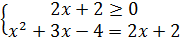<=>  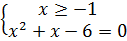<=>  <=> x=2. Ответ: 2

Пример 5.

a )  

Пусть тогда исходное уравнение примет вид:  корни которого y=6 и . Решая уравнение , получаем x=3 и x=-4,5.

Ответ:

В следующих примерах используется более сложная замена переменной.

b )  

Перенесем в левую часть все члены уравнения и произведем дополнительные преобразования: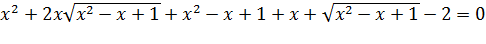  

  

Замена приводит уравнение к виду  корнями которого являются y=1 и y=-2

Осталось решить совокупность двух уравнений:

<=> <=>  <=> x=0

Ответ: {0}

Пример 6 .

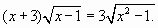
При уравнение принимает вид: которое равносильно совокупности двух уравнений:

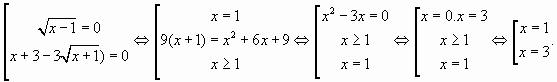
Ответ:

Выделить общий множитель часто бывает очень трудно. Иногда это удается сделать после дополнительных преобразований. В приведенном ниже примере для этого рассматриваются попарные разности подкоренных выражений.

Пример 7 .

Если внимательно посмотреть на уравнение, то можно увидеть, что разности подкоренных выражений первого и третьего , а также второго и четвертого членов этого уравнения равны одной и той же величине

В таком случае далее следует воспользоваться тождеством:

Уравнение примет вид:

или

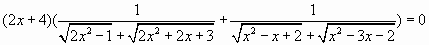
Корень уравнения 2x+4=0 т.е. число x=-2 при подстановке в исходное уравнение дает верное равенство.

Уравнение 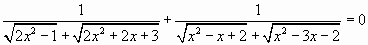не имеет решений, так как его левая часть положительна в своей области определения.

Ответ: {-2}.

Пример 8 .

Преобразуем уравнение следующим образом:

или

Обозначим 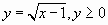и решим полученное уравнение методом интервалов.

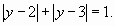
Разбирая отдельно случаи , находим, что решениями последнего уравнения являются  .

Возвращаясь к переменной , получаем неравенства

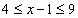
Ответ:

 

Пример 9.

a) Решить неравенство:

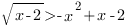
Это неравенство второго типа, оно равносильно совокупности двух систем:

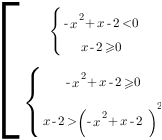
Решим каждое неравенство:

1.  <=>

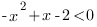
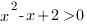
D=1-8=-7, старший коэффициент больше нуля, следовательно это неравенство верно при любом значении х. Решением первой системы будет решение ее второго неравенства: x≥2.

2. 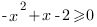Очевидно, что это неравенство не имеет решений. Следовательно, и вся вторая система не имеет решений.

Ответ: x≥2.

b ) Решить неравенство:

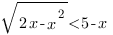
Это иррациональное неравенство первого типа, и оно равносильно системе трех неравенств:

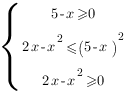
Решим каждое неравенство:

1. <=>

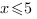
2. <=> <=>

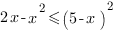
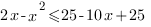
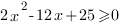
D=144-200<0, следовательно, это неравенство верно при любом значении х.

3.

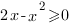
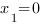
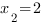
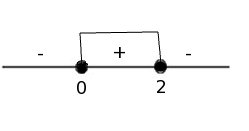
Совместим решения первого и третьего неравенств системы на одной координатной прямой:

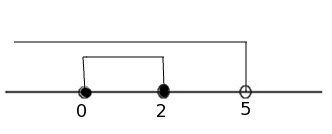
Ответ: 0≤ x ≤ 2.

 

c )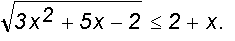

Решение.

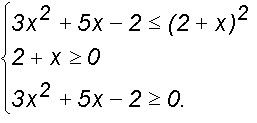
Таким образом необходимо рассмотреть два квадратных и одно линейное неравенство. Их решение не представляет никаких сложностей.

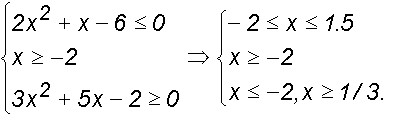
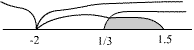
Объединением этих неравенств будет {-2} 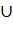 [1/3, 1.5].

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Укажите решение уравнения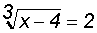

а) 9

б) 12

в) 8

г) 3

2. Иррациональным называется уравнение, где переменная находится:

а) В знаменателе дроби

б) В степени числа

в) Под знаком модуля

г) Под знаком корня

3. Укажите решение уравнения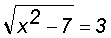

а) 4

б) -4

в) -4; 4

г) 9

4. Корни какой степени не существуют, если выражение, стоящее под знаком корня положительно?

а) Четной

б) Нечетной

в) Четной и нечетной

г) Все существуют

5. Корни какой степени не существуют, если выражение, стоящее под знаком корня отрицательно?

а) Четной

б) Нечетной

в) Четной и нечетной

г) Все существуют

6. Укажите решение неравенства .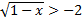

а) x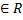

б) x<-3

в) x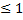

г) x>-3

7. Укажите решение неравенства .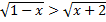

а) x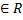

б) 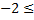x<-1/2

в) x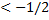

г) -2<x<-1/2

Задачи для самостоятельного решения.

1. Укажите, какому промежутку принадлежит сумма корней уравнения (или корень, если он один):

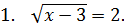
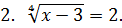
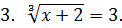
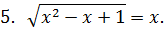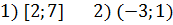
2.  Укажите количество корней уравнения.

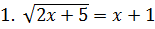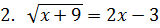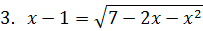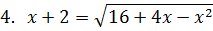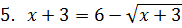
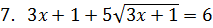
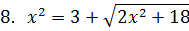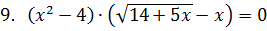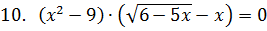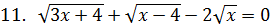
3. Решите неравенства:

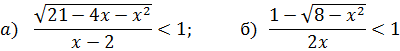
Литература

1. Алгебра и начала математического анализа: учеб. для 10-11кл. общеобразоват. учреждений / [А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.]: под ред. А.Н.Колмогорова.- М.: Просвещение, 2008

2. Алгебра и начала математического анализа. 11 класс. В 2ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А.Г.Мордкович, П.В.Семенов. - М.: Мнемозина, 2009

3. Алгебра и начала математического анализа. 11 класс. В 2ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) / А.Г.Мордкович, П.В.Семенов. - М.: Мнемозина, 2009

4. Алгебра и начала анализа: сборник задач для подготовки и проведения итоговой аттестации за курс средней школы / И.Р.Высоцкий, Л.И.Звавич, Б.П.Пигарев и др.;под ред. С.А. Шестакова. - М.: Внешсигма-М, 2007

5. ЕГЭ. Математика. Показательные и логарифмические выражения, функции, уравнения и неравенства / Е.А.Семенко, М.В.Фоменко; под ред. Е.А.Семенко. - М.: Издательство "Экзамен", 2012

6. Математика. Подготовка к ЕГЭ-2011: учебно-методическое пособие / под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова. - Ростов-наДону: Легион, 2010.

Ключ к тесту

1	2	3	4	5	6	7
б	г	в	г	а	в	б

 

Решение иррациональных уравнений и неравенств

методические рекомендации для учащихся

Составитель

Преподаватель математики

Мочалова Е.В.

Составители: Мочалова Е.В. – преподаватель математики

 

 

От авторов-составителей: Одной из нелегких и трудно усваиваемых тем на уроках математики являются иррациональные уравнения и неравенства. В работе рассмотрены основные понятия и формулы, которые нужно знать для успешного решения иррациональных уравнений и неравенств. Приведены подробные примеры решения некоторых уравнений и неравенств. Подобраны задания для самостоятельного решения и тест для проверки усвоения теоретических основ. Методические рекомендации призваны помочь при самостоятельном изучении и повторении данной темы.

123Следующая ⇒

Поделиться: