
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Понятие об информационно-измерительных системах (ИИС)
2.1 Структура, состав и особенности ИИС ИИС – комплекс средств получения, передачи, обработки и представления информации (позволяет в значительной мере автоматизировать эти процессы с помощью средств вычислительной техники). ИИС – единство аппаратурной части и программного (математического) обеспечения. ИИС используют следующие структурные схемы: Цепочечная (последовательно включенные элементы образуют цепь) Радиальная
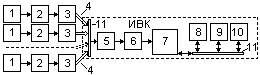
Магистральная Условные обозначения на приведённых выше схемах: 1 – Первичные преобразователи информации (геофизические датчики). 2 – Устройства предварительной обработки данных. 3 – Устройства передачи данных по каналу связи. 4 – Канал связи. 5 – Устройства приёма данных. 6 – Измерительные комплексы. 7 – Вычислительное устройство (ЭВМ). 8 – Устройства накопления и отображения информации. 9 – Устройство управления. 10 – Устройства передачи информации по каналам связи. 11 – Шины. Шины являются важным составной частью ИИС, соединяющей её элементы. В зависимости от передаваемой по шинам информации различают: ~ шины данных, ~ шины команд управления, ~ шины адреса. Конструктивно шина представляет собой группу линий связи в сочетании с блоками управления подключением элементов. На базе шин реализуются схемы интерфейса – основное средство сопряжения элементов ИИС на информационном и программном уровнях. Интерфейс – аппаратурно-программный комплекс, обеспечивающий транспортировку информации и взаимодействие элементов ИИС. Различают: Машинный интерфейс – составная часть ЭВМ, допускающая подключение ограниченного числа устройств, соответствующих Протоколу (шины ISA (устарели), PCI в РС). Приборный интерфейс – подключение к ИИС «внешних» устройств, с учетом рекомендаций международных координирующих организаций (например, МЭК – международная электротехническая комиссия – по использованию стандарта НР: «бит-параллельная, байт-последовательная транспортировка»). По способам управления ИИС делятся на: ~ централизованные – команды управления всеми устройствами вырабатываются одним УУ (простые ИИС, напр. БЭСМ 4). ~ децентрализованные – управление каждым элементом осуществляется собственным УУ (контроллером). Центральное УУ приоритетное координирование (ожидание - активизация) – т.н. адаптивная схема управления. Основные функции ИИС: ~ Подготовка ИИС к работе в конкретной программе измерений (реализуется в режиме диалога с ЭВМ, на которой хранятся пакеты необходимых программ). ~ Проверка и диагностика системы «в целом» (например, проверка нуль- и стандарт-сигналов, собственных шумов, динамического диапазона и т.п.). ~ Измерения и обработка результатов. 2.2 Измерительно-вычислительный комплекс Измерительно-вычислительный комплекс (ИВК) является центральной частью ИИС и представляет собой автоматизированное средство измерения и обработки информации, предназначенное для изучения сложных объектов, представляющее собой совокупность программно-управляемых средств (измерительных, вычислительных, вспомогательных), имеющих определенную внутреннюю организацию; и образующих блочную структуру. Условием формирования ИВК является совместимость её элементов. Различают пять уровней совместимости: ~ Информационная – унификация параметров сигналов, кодов, временных и логических соотношений. ~ Программная – совместимость базового программного обеспечения и всех прикладных программ; согласование правил обмена информацией между программами. ~ Метрологическая – согласование метрологических характеристик всех измерительных устройств и средств обработки информации. ~ Конструктивная – унификация конструктивных решений, разъёмов, механических сопряжений. ~ Энергетическая – унификация параметров питания аппаратуры. Геофизические ИИС часто бывают разорванными на полевую и стационарные части. Передача информации между ними осуществляется либо на промежуточных носителях (магнитные, оптические и др.), либо по общим линиям связи. 2.3 Элементная база ИИС В качестве элементной базы в ИИС используются: ~ интегральные схемы (ИС); ~ большие интегральные схемы (БИС), примером БИС может служить материнская плата персональных компьютеров; ~ микропроцессоры (МкП); ~ в глубинных измерительных устройствах ГИС могут использоваться нувисторы – электронные. Лампы, работающие при высокой температуре). Структура и состав ИС и БИС – индивидуальны. Они определяются выполняемыми функциями и конкретными устройствами, в которых они применяются. Особого внимания заслуживают МкП – универсальный элемент, совершивший революцию в ИИС. На их базе создаются многофункциональные элементы (реализуемые функции определяются выполняемой программой).
Сложность МкП можно оценить на примере процессоров персональных компьютеров Intel Corporation:
В качестве базовых ЭВМ ИВК использовались: 60-е годы – ЭВМ 2-го поколения (БЭСМ-4, М 222, Минск 32 и т.п.) 70-е годы – ЕС ЭВМ (ЕС 1030 – 1061), АСВТ (СМ 4, СМ 2, ПС 2000) в настоящее время – супермикроЭВМ (Work Station: Sun Spark Station, RISK 6000, Silicon Graphics), суперЭВМ. РС используются редко (главным образом в отечественных разработках). 2.4. Принципы транспорта информации в ИИС При организации информационных потоков в ИИС решаются проблемы: ~ выбор рационального метода модуляции, защита от помех; ~ определение необходимой пропускной способности каналов; ~ сжатие, буферирование и хранение данных; ~ вывод информации на устройства отображения и регистрации. Принципиальными являются первые три, рассмотрим их. 2.4.1. Кодирование Наиболее распространённым видом кодирования является различного рода модуляции несущего сигнала: амплитудная (АМ), частотная (ЧМ), широтно-импульсная (ШИМ) и т.п. В геофизических ИИС они используются при передаче сигналов от глубинных датчиков в ГИС и при передаче информации по каналам связи общего назначения. Поэтому на этом виде кодирования в данном пособии останавливаться не имеет смысла. Кодоимпульсная модуляция (частный случай - двоичное кодирование) Суть: преобразование непрерывной во времени-пространстве информации в числовую последовательность (последовательность отсчетов кодируемого параметра геофизического поля). В математике эта задача называется табулированием функций. При преобразовании возникают две проблемы · Выбор точек времени- пространства в которых должны оцифровываться значения измеряемого параметра поля (дискретизация по непрерывному аргументу). · Определение численного значения измеряемого параметра поля в выбранных точках (квантование параметра поля по уровням). Дискретизация по непрерывному аргументу. (для определенности – по времени t) Различают два вида дискретизация: равномерную (эквидистантную), если шаг между точками dt = const (t); неравномерную (неэквидистантную), если dt = vari (t). Выбор шага эквидистантной дискретизации dt определяется теоремой Котельникова (теоремой отсчетов): Функция u (t), допускающая преобразование Фурье и имеющая непрерывный спектр, ограниченный полосой частот 0 ¸ Fc = wc / 2p, полностью определяется дискретным рядом своих значений, взятых через интервал (Доказательство её рассмотривается в курсе «Теоретические основы обработки геофизических данных ») Результатом доказательства теоремы Котельникова является выражение, выражающее непрерывную функцию через её дискретные отсчеты (ряд Котельникова):
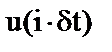 – есть отсчет функции, а сомножитель – есть отсчет функции, а сомножитель 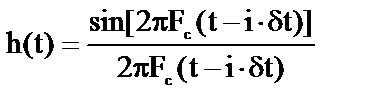 – функция отсчетов (вида f (x) = sin x / x) – функция отсчетов (вида f (x) = sin x / x)
Ряд Котельникова описывает способ восстановления непрерывной функции по её дискретным значениям – низкочастотная фильтрация последовательности прямоугольных импульсов с амплитудами , равными значениям отсчетов, – поскольку правая часть выражения (2) есть дискретная свертка отсчетов функции с функцией отсчетов h(t), которая с физической точки зрения описывает оператор идеального ФНЧ с граничной частотой Fc
(h(t)ÛH(f))
Теорема Котельникова предполагает ограниченность спектра дискретизируемой функции. Однако, согласно одной из теорем о спектрах (теорема масштабов: если f ( t ) Û S ( w ), то S ( w / a ) Û f ( at )) ограниченному спектру соответствует неограниченная по длительности функция. Реальные сигналы в сейсморазведке ограничены по длительности (полуфинитные по природе они являются практически финитными из-за затухания сигналов), т.е. имеют неограниченный спектр.
высокочастотная гармоника Для исключения влияния зеркальных помех шаг дискретизации выбирают равным dt = 1 / 4Fc (т.е при dt =1 мс частотный диапазон составит 0 < f < 250 Гц, при dt =2 м c – 0< f < <125 Гц, при dt =4 мс – 0< f <62,5 Гц), а перед дискретизацией сигнал подвергают НЧ фильтрации с граничной частотой FN = 1 / 2dt (WN = p / dt). Частоту FN (или WN) называют частотой Найквиста, а предварительную НЧ-фильтрацию с частотой FN – антиэлайсинг-фильтрацией. Квантование по уровням Непрерывный сигнал определен на континуальном множестве (т.е он. принимает свои значения из множества действительных чисел), но численные значения его могут быть представлены числами с ограниченной длиной разрядной сетки. Суть квантования по уровням – в отображении непрерывного множества значений сигнала на конечное подмножество того же множества. Алгоритм отображения: ~ X(t) – непрерывный сигнал, значения которого изменяются в интервале x1 £ X(t) £ xm (x 1 ¸ xm – динамический диапазон сигнала) ~ Разобьем интервал x1 ¸ xm на m+1 классов: ~ Поставим в соответствие каждому классу его представителя: yi Î (xi-1, xi). ~ Если амплитуда сигнала в момент оцифровки (tk) попадает в класс Сi (т.е. X(tk) Î Ci), то истинное значение сигнала (X(tk)) заменяется значением представителя класса (yi) При замене возникает ошибка x = yi - X(tk) , величина которой по модулю не превышает размера класса D. Квантованный сигнал можно представить как Y(t)=X(t)+x(t) Вывод: - чем меньше шаг квантования D, тем меньше W (тем ближе квантованный сигнал к исходному); Примечание: число разрядов преобразователей непрерывного (аналогового) сигнала в в дискретную числовую последовательность (преобразователь аналог-код, ПАК) ограничено техническими возможностями (до недавнего времени оно равнялось 14, сейчас используются преобразователи с разрядностью 24). 2.4.2 Пропускная способность каналов связи Надежность передачи информации по каналам связи в значительной мере определяется: ~ шириной частотного диапазона канала (Fk); Согласно теореме Шеннона о кодировании в канале с помехами, наличие помехи не влияет на точность передачи, а лишь снижает её скорость. Скорость передачи (измеряется в бодах = 1 имп. в сек.): Вс=1/dt (4), = Максимальная скорость передачи в канале может быть определена как:
(здесь t с..и. – время спада импульса). Минимальная длительность импульса t имп. min » 2 tн.и., т.е. (1/ tн.и.) »2Fk
Для случайной помехи типа «белый шум» Шенноном было определено значение Вс. max как 2.4.3. Уплотнение каналов связи. Сжатие данных. Буферирование. Проблема уплотнения каналов возникает там, где по ограниченному числу жил соединительного кабеля (шины) необходимо передать информацию от многих источников в один и тот же интервал времени. = Различают два вида уплотнения: ~ Временной: n = dtc / k×Dt k (8), Способ эффективен, если ×Dt k << dtc (Dt k определяется конструктивными особенностями канала связи, dtc - верхней границей спектра сигнала). Широко использовался в мультиплексных системах регистрации. Сжатие данных применяется для экономичного хранения и передачи информации, если спектральные характеристики сейсмозаписи меняются вдоль оси времен. Пусть интервал времени регистрации сейсмотрассы разбит на участки Т1, Т2, Т3, Т4, где верхняя граница спектра F1, F2, F3, F4 соответственно, причем F1,> F2,> F3,> F4.
где Fmax = sup { F1, F2, F3, F4 }. Тогда число отсчетов на трассе N = Nmax = Другой вид сжатия – экстремальное кодирование: оцифровываются только экстремальные значения сигнала, т.е. dtj = 1 / 2 F*j, где j – индекс сигнала упругой волны, а F*j – видимая частота j-того сигнала. Так как F*j значительно ниже верхней границы спектра, то N<<Nmax, и, кроме того, шаг дискретизации изменяется в соответствии с изменением частотных характеристик сигнала. Третий вид уплотнения – оцифровка только сигналов регулярных волн (наиболее эффективный и наиболее сложный вид уплотнения, т.к. необходимо формальное описание регулярного сигнала). В полной мере он реализован только в комплексе обрабатывающих программ SWAP. Буферирование данных Согласно основной теореме Шеннона о кодировании в канале без помех, если скорость поступления информации (Си) больше скорости её переработки в ИИС (Ск), то необходимо накопление информации в буферной памяти. Построение каналов с Ск > Си не всегда рационально (а иногда и нереально), т.к. накопление в буфере может быть более оптимальным с технической и экономической точек зрения (Пример : ограниченная пропускная способность регистратора в сейсмостанции Прогресс-96 потребовала НЦС). РЕЗЮМЕ: Для определения характеристик ИИС необходимо знать параметры регистрируемых сигналов (tимп, S(w), D и т.п.).
2.5. Сейсморазведочные ИИС как линейные системы Как известно, прямая задача геофизических методов разведки (в т.ч. и сейсморазведки) описывается выражением Целью геофизической разведки является решение обратной задачи – нахождение модели среды по наблюденному полю ( Существующие методы решения обратных задач предполагают линейность оператора прямой задачи. Т.Е.: сейсмическая разведка и сейсморазведочные ИИС рассматриваются как линейные системы. (Предположение о линейности свойств среды лежит и в основе теории сейсмических волновых полей). Сейсморазведочные ИИС в своей регистрирующей части осуществляют линейные преобразования: uвых = L{uвх} (11), Свойства линейных преобразований (по Ю.В. Напалкову) 1. Аддитивность: Если L{xi} = yi, то L{x1+x2}=L{x1}+L{x2} или в общем виде: 2. Однородность: L{nx} = nL{x} (13) Операции над линейными преобразованиями. ~ Сумма линейных преобразований L1 и L2 есть линейное преобразование L, сопоставляющее величины x и y в соответствии с равенством y = L1{x} + L2{x}, т.е. ~ Произведение линейных преобразований L1 и L2 есть линейное преобразование L, которое получается путем последовательного применения преобразований L1 и L2 {x}: ~ Сумма и произведение линейных преобразований – также линейное преобразование: L = L1 + L2 L{x1 + x2} = L1{x1 + x2} + L2{x1 + x2} = L1{x1} + = L{x1} + L{x2} (16) Следствие из (16): L = L2×L1 L{x1 + x2} = L2{L1{x1 + x2}} = L2{L1{x1} + Следствие из (18): L{n×x} = (L2L1){n×x} = L2{L1{n×x}} = Принцип суперпозиции вытекает из аддитивности линейного преобразования и предполагает независимость прохождения нескольких сигналов через линейную систему: – Если через линейную систему, осуществляющую преобразование L, проходит несколько сигналов (n), то каждый из них (i-тый) независимо от других создает на выходе системы сигнал yi = L{xi}, а результирующий сигнал на выходе системы (в соответствии с (12)) будет являться суперпозицией отдельных выходных сигналов: y = Опираясь на принцип суперпозиции можно оценить реакцию линейной системы на прохождения сложного сигнала как сумму реакций на составляющие сложного сигнала. Чаще всего в качестве составляющих рассматриваются либо единичные импульсы, либо гармонические функции (последние являются основой спектрального анализа). 2.6. Характеристики сейсморазведочных ИИС Известно, что линейные системы описываются дифференциальными уравнениями с постоянными коэффициентами, если их характеристики неизменны (стационарны) во времени. Во временной области линейные системы полностью определяются переходной функцией (импульсной реакцией): h(t) – реакция системы на единичный импульс (рассчитывается путем решения дифференциального уравнения при заданном входном сигнале). В частотной области линейные системы описываются комплексной частотной характеристикой H(w) = |H(w)|×e- jj(w) (21), Импульсная реакция h(t) и комплексная частотная характеристика H(w) связаны парой преобразований Фурье:
ü ý
Численно линейные системы описываются следующими характеристиками (параметрами): = Коэффициент передачи (коэффициент усиления) = Номинальный выходной сигнал ( U вых. ном) – наибольший сигнал на выходе системы при котором искажения сигнала не превышают заданной величины (как правило – 2%) = Номинальный входной сигнал ( U вх. ном) – сигнал на входе системы, при котором сигнал на выходе равен Uвых. ном. = Входное сопротивление (импеданс) – полное входное сопротивление системы для гармонического сигнала (импеданс частотнозависим!). = Нелинейные искажения возникают при прохождении через систему сигнала из-за нелинейности характеристик её элементов; проявляются в появлении на выходе системы высших гармоник, если на вход подан гармонический сигнал. Их величина измеряется коэффициентом нелинейных искажений (КНИ): = Динамический диапазон = Частотная характеристика системы (АЧХ системы)
Различают нижнюю = Ширина полосы пропускания: Dw = = Средняя (резонансная) частота: частота w рез , при которой U вых = U max . = Крутизна частотной характеристики в области её склонов характеризует быстроту перехода от ПП к ПГ. Определяется в логарифмических величинах (дб / окт): Конкретный вид характеристик ИИС и конкретные значения параметров определяются прежде всего исходной информацией (в нашем случае – сейсмическим сигналом) Контрольные вопросы 1. Что понимается по ИИС? 2. Какие структурные схемы ИИС вам известны? 3. Какие основные элементы входят в состав ИИС? 4. Каково назначение шин и какие виды шин вам известны? 5. Назначение интерфейса в ИИС? 6. Какие типы интерфейса в ИИС вам известны 7. Каковы основные функции реализуют ИИС? 8. Что понимается под ИВК? 9. Каковы уровни совместимости элементов ИВК? 10. Что используется в качестве элементной базы ИИС? 11. В чём отличия ИС и БИС? 12. Какова структурная схема микропроцессора? 13. Какие виды ЭВМ используются в ИИС в качестве базовых в настоящее время? 14. Какие проблемы решаются при организации информационных потоков в ИИС? 15. В чём суть кодоимпульсной модуляции? 16. В чём суть дискретизации непрерывного сигнала по непрерывному аргументу? 17. В чём суть квантования сигналов по уровням? 18. Формулировка теоремы Котельникова? 19. Напишите выражение для ряда Котельникова. 20. Напишите выражение для функции отсчётов. 21. Каков физический смысл функции отсчётов? 22. Что понимается под «зеркальной помехой», в чём проявляется её искажающее влияние? 23. Какими мерами ослабляется влияние зеркальных помех? 24. В чём суть квантования по уровням? 25. Что понимается под «уровнем квантования»? 26. Из каких соображений выбирается шаг квантования? 27. Чем определяется максимальная скорость передачи информации в канале связи? 28. Чем обусловлена потребность в уплотнении канала связи? 29. Какие виды уплотнения каналов вам известны? 30. С какой целью используется сжатие данных в канале связи? 31. Какие виды сжатия данных вам известны? 32. С какой целью используется буферирование данных в канале связи? 33. На что влияет присутствие помехи при передаче данных и чем это доказано? 34. Какие системы называются линейными? 35. Чем обусловлено рассмотрение сейсморазведочных ИИС как систем линейных? 36. Свойства линейных преобразований. 37. Какие операции выполняются над линейными преобразованиями? 38. В чём суть принципа суперпозиции? 39. Какими функциональными характеристиками описывается действие ИИС? 40. Запишите выражение, связывающее импульсную и комплексную частотную характеристики ИИС. 41. Что понимается под коэффициентом передачи системы? 42. Что понимается под номинальным выходным сигналом? 43. Что понимается под номинальным входным сигналом? 44. Что понимается под импедансом системы? 45. Что понимается под коэффициентом нелинейных искажений? 46. Что понимается под динамическим диапазоном системы? 47. Что характеризует уровень шумов, приведённый ко входу системы? 48. Что понимается под граничными частотами частотной характеристики системы? 49. Что называется полосой пропускания частотной характеристики системы? 50. Что понимается под резонансной частотой системы? 51. Что характеризует крутизна частотной характеристики? 52. В чём измеряется крутизна частотной характеристики?
|
Последнее изменение этой страницы: 2019-04-19; Просмотров: 437; Нарушение авторского права страницы