Эквивалентность определений предела по Коши и по Гейне.
Теорема. Определения по Коши и по Гейне эквивалентны.
Пример. Доказать по определению 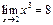 .
.
Запишем определение:  . Когда значения нашей функции принадлежат
. Когда значения нашей функции принадлежат 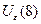 , аргумент
, аргумент 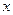 принадлежит интервалу
принадлежит интервалу 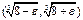 . Нам необходимо найти максимальный размер окрестности
. Нам необходимо найти максимальный размер окрестности 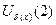 принадлежащий указанному интервалу. Окрестность
принадлежащий указанному интервалу. Окрестность 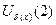 - интервал симметричный относительно числа 2. Используя график функции и изображения окрестностей, находим, что
- интервал симметричный относительно числа 2. Используя график функции и изображения окрестностей, находим, что 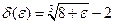 .
.
Критерий Коши существования предела функции.
Теорема. (Критерий Коши). Для того, чтобы существовал конечный предел 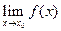 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 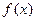 была определена в некоторой окрестности точки
была определена в некоторой окрестности точки 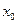 , быть может кроме самой этой точки, и
, быть может кроме самой этой точки, и 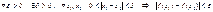
Теорема об ограниченности функции, имеющей конечный предел.
Теорема. Если 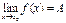 , где
, где 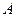 - конечное число, то на некоторой окрестности
- конечное число, то на некоторой окрестности 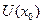
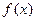 -ограничена, то есть
-ограничена, то есть 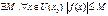 .
.
Доказательство. Пусть 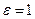 , тогда
, тогда 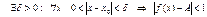 . Преобразуем последнее неравенство:
. Преобразуем последнее неравенство: 
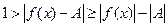 . Отсюда имеем, что для любого
. Отсюда имеем, что для любого 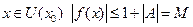 , т.е. функция ограничена числом
, т.е. функция ограничена числом 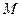 . Теорема доказана.
. Теорема доказана.
Теорема о сохранении знака функции, имеющей конечный предел
Теорема. (О сохранении знака). Если 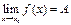 , где
, где 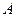 - конечное число, то на некоторой окрестности
- конечное число, то на некоторой окрестности 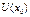
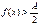 , если
, если 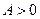 , и
, и 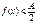 , если
, если 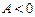 .
.
Доказательство.Пусть 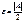 , тогда
, тогда 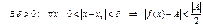 . Последнее неравенство запишем в виде:
. Последнее неравенство запишем в виде: 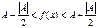 . Если
. Если 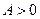 , то из левого неравенства имеем
, то из левого неравенства имеем 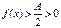 . Если
. Если  , то из правого неравенства имеем
, то из правого неравенства имеем  . Теорема доказана.
. Теорема доказана.
Теорема о зажатой функции.
Теорема. (О зажатой функции). Если 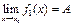
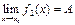 и на некоторой окрестности
и на некоторой окрестности 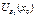
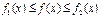 ,тогда
,тогда 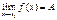 .
.
Непрерывность функции. Непрерывность сложной функции
Определение. Функция 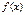 непрерывна в точке
непрерывна в точке 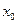 , если она определена в некоторой окрестности этой точки, в том числе и в самой тоске
, если она определена в некоторой окрестности этой точки, в том числе и в самой тоске 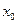 , и если
, и если 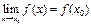 , т.е.
, т.е. 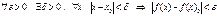 .
.
Из определения следует, что для непрерывной функции справедливо равенство:
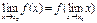 , то есть предел можно вносить в аргумент непрерывной функции.
, то есть предел можно вносить в аргумент непрерывной функции.
Определение*. Функция 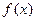 непрерывна в точке
непрерывна в точке 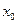 , если она определена в некоторой окрестности этой точки, в том числе и в самой тоске
, если она определена в некоторой окрестности этой точки, в том числе и в самой тоске 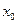 , и если ее приращение в этой точке, соответствующее приращению аргумента
, и если ее приращение в этой точке, соответствующее приращению аргумента 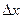 , стремится к нулю при
, стремится к нулю при 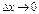 , т.е.
, т.е. 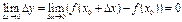 .
.
Теорема. Если 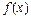 и
и 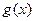 непрерывны в точке
непрерывны в точке 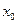 , то непрерывны их сумма, разность, произведение и частное.
, то непрерывны их сумма, разность, произведение и частное.
Теорема. (О непрерывности сложной функции). Пусть задана функция 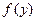 , непрерывная в точке
, непрерывная в точке 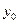 , и функция
, и функция 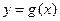 , непрерывная в точке
, непрерывная в точке 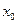 , и пусть
, и пусть 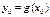 . Тогда сложная функция
. Тогда сложная функция 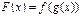 непрерывна в точке
непрерывна в точке 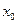 .
.
Классификация точек разрыва. Примеры
Разрывы бывают устранимые и неустранимые. Отличают неустранимые разрывы первого и второго рода.
Функция 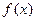 в точке
в точке 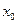 имеет устранимый разрыв, если предел слева равен пределу справа и не равен значению функции в точке
имеет устранимый разрыв, если предел слева равен пределу справа и не равен значению функции в точке 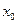 . Такой разрыв можно устранить, изменив значение функции в одной точке. Пример:
. Такой разрыв можно устранить, изменив значение функции в одной точке. Пример: 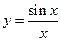 .
.
Функция 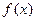 в точке
в точке 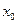 имеет неустранимый разрыв первого рода, если конечный предел слева не равен конечному пределу справа. Пример:
имеет неустранимый разрыв первого рода, если конечный предел слева не равен конечному пределу справа. Пример: 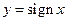 .
.
Функция 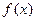 в точке
в точке 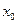 имеет неустранимый разрыв второго рода, если хотя бы один из пределов не существует или равен
имеет неустранимый разрыв второго рода, если хотя бы один из пределов не существует или равен 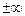 . Примеры:
. Примеры: 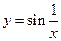 ;
; 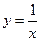 .
.
Замечательные пределы.
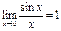 - первый замечательный предел.
- первый замечательный предел.
Используя тригонометрический круг, определение синуса и тангенса, а также неравенство 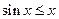 , можно при
, можно при 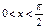 записать выражение
записать выражение 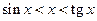 . Разделим его на
. Разделим его на 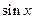 и получим
и получим 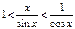 . По теореме о зажатой функции имеем
. По теореме о зажатой функции имеем 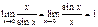 .
.
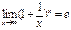 -второй замечательный предел.
-второй замечательный предел.
Следует из определения числа 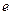 . Можно показать, что переменной может быть не только натуральное число, но и действительное число, стремящееся к
. Можно показать, что переменной может быть не только натуральное число, но и действительное число, стремящееся к 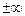 .
.
19.Сравнение бесконечно малых.
Определение. Если 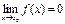 , то говорят, что
, то говорят, что 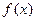 бесконечно малая при
бесконечно малая при 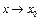 .
.
Определение. Если 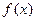 и
и 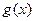 - бесконечно малая при
- бесконечно малая при 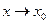 и
и 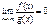 , то говорят, что
, то говорят, что 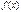 - о- малое от
- о- малое от 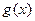 при
при 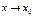 , т.е.
, т.е. 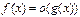 при
при 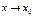 .
.
Определение. Если 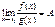 , где
, где 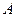 - конечное число, то говорят, что
- конечное число, то говорят, что 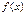 и
и 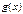 величины одного порядка малости при
величины одного порядка малости при 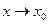 .
.
Определение. Если 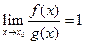 ,
, 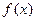 эквивалентна
эквивалентна 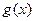 при
при 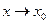 , т.е.
, т.е. 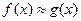 при
при 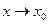 .
.
Примеры эквивалентных бесконечно малых при 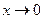 :
: 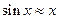 ;
; 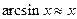 ;
; 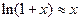 ;
; 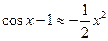 ;
; 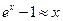 ;
; 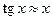 .
.
Определение. Если 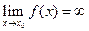 , то говорят, что
, то говорят, что 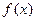 бесконечно большая величина при
бесконечно большая величина при 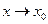 .
.

