
| | Жан Бернард Леон Фуко (1819–1868)
| Тот факт, что Земля вращается вокруг своей оси, сегодня известен каждому школьнику. Однако не всегда люди были убеждены в этом: обнаружить вращение Земли, находясь на ее поверхности, достаточно трудно. Конечно, можно догадываться, что суточное движение небесных тел по небесной сфере – это и есть проявление вращения Земли. Но видится нам это явление именно как движение Солнца и звезд по небу.
В середине XIX века Жан Бернард Леон Фуко смог провести опыт, который демонстрирует вращение Земли достаточно наглядно. Опыт этот был проведен неоднократно, а публично сам экспериментатор представил его в 1851 году в здании Пантеона в Париже.

| | Рис. 1. Маятник Фуко в парижском Пантеоне
| Здание Парижского Пантеона в центре венчает громадный купол, к которому была прикреплена стальная проволока длиной 67 м. К этой проволоке подвесили массивный металлический шар. По разным источникам, масса шара составляла от 25 до 28 кг. Проволока крепилась к куполу таким образом, чтобы получившийся маятник мог качаться в любой плоскости.
Маятник совершал колебания над круглым постаментом диаметром 6 м, по краю которого был насыпан валик из песка. При каждом качании маятника острый стержень, укрепленный на шаре снизу, оставлял на валике отметку, сметая с ограждения песок.

| | Рис. 2. Плоскость качаний маятника Фуко постепенно поворачивается относительно земного наблюдателя
| Для того, чтобы исключить влияние подвеса на маятник Фуко, применяют специальные подвесы (рис. 4). А для того, чтобы избежать бокового толчка (то есть, чтобы маятник качался строго в плоскости), шар отводят в сторону, привязывают к стене, а затем пережигают веревку.
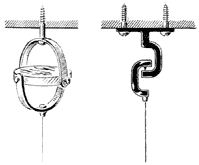
| | Рис. 3. Подвес маятника Фуко и начало его движения
| Период колебаний маятника, как известно, может быть рассчитан по формуле:
Подставляя в эту формулу длину маятника l = 67 м и значение ускорения свободного падения g = 9,8 м/с2, получаем, что период колебаний маятника в опыте Фуко составлял T ≈ 16,4 с.
По прошествии каждого периода новая отметка, производимая острием стержня на песке, оказывалась примерно в 3 мм от предыдущей. За первый час наблюдений плоскость качаний маятника повернулась на угол около 11° по часовой стрелке. Полный же оборот плоскость маятника совершила примерно за 32 часа.
Опыт Фуко производил огромное впечатление на наблюдавших его людей, которые будто бы непосредственно ощущали движение земного шара. Среди зрителей, наблюдавших опыт, был и Л. Бонапарт, через год провозглашенный императором Франции Наполеоном III. За проведение опыта с маятником Фуко был удостоен Ордена Почетного легиона – высшей награды Франции.
В России маятник Фуко длиной 98 м был установлен в Исакиевском соборе в Ленинграде. Обычно показывался такой удивительный эксперимент – устанавливался на полу спичечный коробок чуть поодаль от плоскости вращения маятника. Пока гид рассказывал о маятнике, плоскость его вращения поворачивалась и стержень, укрепленный на шаре, сбивал коробок.
В основу опыта был положен уже известный в то время экспериментальный факт: плоскость качания маятника на нити сохраняется независимо от вращения основания, к которому подвешен маятник. Маятник стремится сохранить параметры движения в инерциальной системе отсчета, плоскость которой неподвижна относительно звезд. Если поместить маятник Фуко на полюсе, то при вращении Земли плоскость маятника будет оставаться неизменной, и наблюдатели, вращающиеся вместе с планетой, должны видеть, как плоскость качаний маятника поворачивается без воздействия на него каких-либо сил. Таким образом, период вращения маятника на полюсе равен периоду обращения Земли вокруг своей оси – 24 часам. На других широтах период будет несколько больше, т. к. на маятник действуют силы инерции, возникающие во вращающихся системах – силы Кориолиса. На экваторе плоскость маятника вращаться не будет – период равен бесконечности.
26. Гидростатика — это частный случай гидроаэромеханики, где изучается равновесие жидкостей и газов, т. е. их скорость равна нулю.
Виды жидкостей
Несжимаемая жидкость — это жидкость или газ, где зависимость плотности от давления не имеет никакого значения.
Сжимаемая жидкость — это газ, где зависимость плотности от давления имеет большое значение.
Идеальная жидкость — это жидкость, где нет внутреннего трения.
Вязкая жидкость — это жидкость, где присутствует внутреннее трение.
Баротропная жидкость — это жидкость, где плотность имеет зависимость только от давления.
Давление — это физическая величина, которая характеризует силу, перпендикулярную поверхности, и ее действие на каждую единицу этой поверхности: 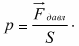
В Международной системе СИ единица давления — это паскаль (Па).
Гидростатическое давление — это давление, которое создается жидкостью, которая при воздействии силы тяжести, остается в равновесии.
Гидростатическое давление определяется следующей формулой:
 , где h — высота жидкости, p — плотность жидкости. , где h — высота жидкости, p — плотность жидкости.
Давление жидкости на высоте h определяется формулой:

Закон Архимеда: выталкивающая сила, которая действует на тело, погруженное жидкость или газ, равна весу жидкости в объеме погруженного тела, эта сила направлена вверх и приложена к центру тяжести вытесненного объема жидкости или газа.

Агрегатные состояния вещества
Фазовый переход, или превращение — это переход вещества из одного агрегатного состояния в другое. При этом фазовый переход первого рода имеет скачкообразное изменение внутренней энергии и плотности, это связано с выделением или поглощением теплоты фазового перехода, а фазовый переход второго рода не обнаруживает скачкообразное изменение внутренней энергии и плотности, теплота фазового перехода равна нулю, при этом переходе скачкообразно меняются теплоемкость и термодинамические коэффициенты, которые являются характеристиками относительного изменения объема системы.
Жидкость — это тела, которые имеют определенный объем, но не имеют упругости формы.
Поверхностное натяжение — это свойство, обусловленное сила- ми притяжения между молекулами.
Сила поверхностного натяжения — это сила, действующая вдоль поверхности жидкости перпендикулярно линии, которая ограничивает эту поверхность.
Коэффициент поверхностного натяжения — это физическая величина, определяемая отношением модуля силы поверхностного натяжения, которая оказывает воздействие на границу поверхностного слоя длиной, к этой длине:
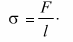
Смачивание — это процесс, появляющийся на границе соприкосновения жидкостей с твердыми телами, другими жидкостями и газами, которое определено взаимодействием молекул на границе контактирующих сред. Капиллярные явления — это процессы, определенные поверхностным натяжением и совершающиеся в тонких узких трубках, т. е. (капиллярах).
Высота подъема или опускания жидкости в капилляре обратно пропорциональна радиусу капилляра и плотности жидкости, определяется:
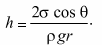
Парообразование — это переход вещества из жидкого состоя- ния в газообразное.
Существуют два типа парообразования:
Испарение — это явление перехода вещества из жидкого состояния в газообразное, совершающееся со свободной поверхности жидкости при любой температуре.
Пар (газ) — это совокупность молекул, которые вылетают из жидкости.
Факторы, от которых зависит испарение:
- если температура повышается, то скорость испарения увеличивается;
- если создавшийся пар сдувается потоком воздуха или откачивается, то скорость испарения возрастает;
- если площадь свободной поверхности жидкости больше данного объема, то испарение происходит быстрее.
Теплота испарения или парообразования — это количество теплоты, которую нужно сообщить жидкости при данной температуре и давлении, чтобы перевести ее в пар той же температуры и при том же давлении.
Кипение — это интенсивное испарение жидкости, совершающееся не только с ее свободной поверхности, но и во всем объеме жидкости внутри образующихся при этом пузырьков пара.
Кипение жидкости начинается при такой температуре, когда выполняется условие:

Теплота испарения (теплота парообразования) — это количество теплоты, которое нужно сообщить веществу, с тем чтобы перевести его из жидкого состояния в газообразное.
Удельная теплота парообразования — это количество теплоты, которое необходимо для превращения вещества единичной массы из жидкого состояния в пар при температуре кипения.
Конденсация — это переход вещества вследствие его охлаждения или сжатия из газообразного состояния в жидкое или твердое.
Разбавленный раствор — это смесь нескольких веществ, в которой одно из веществ является преобладающим, а остальные являются малыми примесями.
Явление осмоса — это проникновение растворителя в раствор через пористую перегородку, плотную для растворенного вещества и отделяющую раствор от чистой жидкости.
Сверхтекучесть — это процесс практически полного отсутствия вязкости, обнаруженного у жидкого гелия.
Твердые тела бывают двух типов:
- кристаллические;
- аморфные.
Кристаллы — это твердые тела, обладающие правильным периодическим расположением собирающих их частиц.
Типы кристаллов:
- металлы, в которых валентные электроны оставляют атомы, делаются коллективизированными, образуя электронный газ в металлах;
- ионные кристаллы, которые характеризуются ионной связью между правильно чередующимися в узлах кристаллической решетки положительными и отрицательными ионами;
- валентные кристаллы, характеризуются гомеополярной связью;
- молекулярные кристаллы в узлах кристаллической решетки которых находятся молекулы;
- кристаллы с водородными связями — это формирование связи, которое происходит так, что атом водорода передает свой электрон одному из атомов молекулы, водородная связь создастся в основном за счет ионного взаимодействия с образующимся ионом водорода.
Тепловое расширение — это изменение линейных размеров и объемов тел, которые возникают за счет нагревания.
Теплопроводность — это вид теплообмена, который в результате приводит к выравниванию температур различных частей тела, в процессе которого происходит передача энергии от более нагретых частей к менее нагретым.
Коэффициент электронной теплопроводности для металлов, когда происходит классическое приближение идеального электронного газа:


теплового движения электронов.
Теплота плавления — это количество теплоты, необходимое для вещества, чтобы перевести его из твердого кристаллического состояния в жидкое.
Кристаллизация — это явление перехода вещества из жидкого состояния в твердое кристаллическое.
Кристаллизация — процесс, обратный плавлению, который происходит при постоянной температуре, равной температуре плавления.
Адсорбция — это концентрирование одного из веществ, совершающееся в смежном слое у поверхности раздела двух фаз. Десорбция — это явление, обратное адсорбции, абсорбция характе- ризуется как объемное поглощение вещества.
Жидкие кристаллы — это состояние отдельных органических веществ, которые находятся в процессе перехода из жидкого состояния в твердое кристаллическое не сразу, а через промежуточные состояния, которым свойственны свойства как жидкостей, так и кристаллов.
Аморфные вещества — это вещества, не имеющие в конденси- рованном состоянии кристаллическое строение, но обладающие упругостью формы.
Структурное стеклование — это перевод аморфного вещества из жидкого состояния в твердое, если осуществляется изменение температуры или давления.
Размягчение — это обратный стеклованию процесс.
Полимеры — это вещества, молекулы которых построены из большого числа повторяющихся групп Равновесие тела в покоящейся жидкости
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела. Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
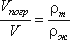 где: V - объем плавающего тела; ρm - плотность тела. где: V - объем плавающего тела; ρm - плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называетсяостойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения. При нормальном положении судна центр тяжестиС и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.
 Рис. 2.5. Поперечный профиль судна Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) еслиh<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, темЗакон Паскаля. Давление, приложенное к жидкости (или газу), находящейся в ограниченном объёме, передаётся во все точки внутри объёма без изменения. Например, если несжимаемая жидкость плотностью r помещена в атмосферу, то давление на глубине h согласно закону Паскаля будет равно P P gh = +r A , где PA – атмосферное давление. На законе Паскаля основано действие гидравлического подъёмника (рис. 4). Подъёмник состоит из двух сообщающихся сосудов, залитых несжимаемой жидкостью (обычно маслом). Площади сечения сосудов соответственно равны S1 и S2 ( S S 1 2 << ). Поднимаемый груз кладут на широкий поршень, а силу прикладывают к узкому. Посчитаем силу, необходимую для того, чтобы удерживать груз массы M неподвижно. Если поршни находятся на одном уровне, то давления под ними должны быть A B h Вакуум Рис.3. Принципиальная схема жидкостного барометра. Mg F M S1 S2 Рис. 4. Принцип работы гидравлического подъёмника. одинаковы: P P 1 2 = . Но P F S 1 1 = , а P Mg S 2 2 = . Отсюда получаем, что F Mg S S = 1 2 . Т.к. S S 1 2 << , то и F << Mg . Заметим, однако, что так как объем жидкости при подъёме груза не меняется, то для того, чтобы поднять груз на небольшую высоту, приходится поршень S1 опускать на значительную глубину. Важное замечание. Закон Паскаля не утверждает, что давление жидкости одинаково в каких-либо областях. Он утверждает, что если давление приложено к какой-то одной части жидкости, то оно возрастает на эту величину во всех местах в жидкости, т.е. передаётся жидкостью.. Закон Архимеда
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:
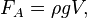
где 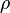 — плотностьжидкости (газа), — плотностьжидкости (газа), 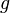 — ускорение свободного падения, а — ускорение свободного падения, а 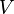 — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена кцентру тяжестиэтого объёма. — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена кцентру тяжестиэтого объёма.
 Тело плавает, если сила Архимеда уравновешивает силу тяжести тела. Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
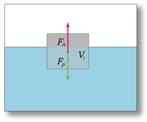
Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.
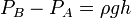 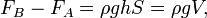
где PA, PB — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.
Плавание тел
По закону Архимеда на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх,

 где W— объем погруженной части тела. где W— объем погруженной части тела.
Вес воды, вытесняемой телом, полностью или частично погруженным в воду, называется водоизмещением.
Центр тяжести 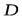 вытесненного объема жидкости называетсяцентром водоизмещения илицентром давления. При наклоне (крене) плавающего тела центр водоизмещения изменяет свое положение. вытесненного объема жидкости называетсяцентром водоизмещения илицентром давления. При наклоне (крене) плавающего тела центр водоизмещения изменяет свое положение.
Линия, проходящая через центр тяжести тела  и центр водоизмещения и центр водоизмещения 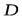 в положении равновесия перпендикулярно свободной поверхности воды (плоскости плавания), являетсяосью плавания. В положении равновесия ось плавания вертикальна, при крене она наклонена к вертикали под углом крена. в положении равновесия перпендикулярно свободной поверхности воды (плоскости плавания), являетсяосью плавания. В положении равновесия ось плавания вертикальна, при крене она наклонена к вертикали под углом крена.
Точку пересечения подъемной силы Р при наклонном положении тела с осью плавания принято называтьметацентром.Расстояние между центром тяжести тела  и метацентромMобозначается черезhм(метацентрическая высота). Чем выше расположен метацентр над центром тяжести тела, т. е. чем больше метацентрическая высота и метацентромMобозначается черезhм(метацентрическая высота). Чем выше расположен метацентр над центром тяжести тела, т. е. чем больше метацентрическая высота 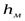 , тем больше остойчивость тела (способность из крена переходить в положение равновесия), так как момент пары сил , тем больше остойчивость тела (способность из крена переходить в положение равновесия), так как момент пары сил 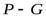 , стремящийся восстановить равновесие тела, прямо пропорционален метацентрической высоте. Величина метацентрической высоты может быть определена по формуле , стремящийся восстановить равновесие тела, прямо пропорционален метацентрической высоте. Величина метацентрической высоты может быть определена по формуле

где 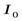 — момент инерции площади плоскости плавания относительно продольной оси — момент инерции площади плоскости плавания относительно продольной оси 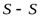 ; ;
W— водоизмещение тела;
е — расстояние между центром тяжести и центром водоизмещения.
Если метацентр лежит ниже центра тяжести тела, т. е. метацентрическая высота отрицательна, то тело неостойчиво.
27. Гидродинамика – раздел гидравлики, изучающий законы движения жидкости и ее взаимодействия с неподвижными и подвижными поверхностями.
Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.
В целях упрощения расчета вводится понятие струйчатой модели движения. Согласно этой модели поток состоит из отдельных элементарных струек, изучение которых в отдельности дает возможность понять закономерности потока в целом.
Основными уравнениями гидродинамики являются уравнение неразрывности (сплошности) и уравнение Бернулли.
Уравнение неразрывности есть уравнение постоянства расхода.
1. Для элементарной струйки

или
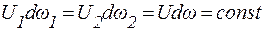 , ,
где U1, U2, U – скорости движения частиц жидкости в отдельных живых сечениях струйки; dw1, dw2, dw - площади живых сечений струйки.
2. Для потока
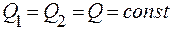
или
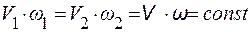 , ,
где V1, V2, V – средние скорости в живых сечениях; w1, w2, w - площади живых сечений потока.
Уравнение Бернулли является фундаментальным уравнением гидродинамики. Оно устанавливает связь между давлением, скоростью и положением жидкости в пространстве. С помощью этого уравнения решается большой круг инженерных задач.
Для упрощения изучения общих закономерностей, присущих особенно движущейся жидкости, ее часто представляют в виде несжимаемой среды, не обладающей внутренним трением. Такую жидкость называют идеальной.
Уравнение Бернулли для элементарной
струйки идеальной жидкости
Расчетная форма этого уравнения имеет вид
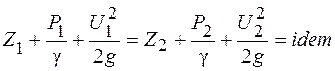 , ,
где Z – геометрический напор, или удельная потенциальная энергия положения; 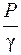 – пьезометрический напор, или удельная потенциальная энергия давления; – пьезометрический напор, или удельная потенциальная энергия давления; 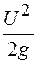 – скоростной напор, или удельная кинетическая энергия. – скоростной напор, или удельная кинетическая энергия.
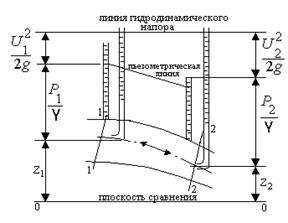 Представим это уравнение графически для элементарной струйки переменного сечения (см рис.1) Представим это уравнение графически для элементарной струйки переменного сечения (см рис.1)
Рис.1.
Это уравнение является уравнением закона сохранения энергии для движущейся жидкости. В этом заключается его физический смысл.
Уравнение Бернулли для элементарной
струйки реальной жидкости
При движении реальной жидкости, обладающей вязкостью, часть ее энергии затрачивается на преодоление сил трения. Эта энергия в виде тепла рассеивается в окружающую среду. Процесс этот необратим и в физике называется диссипацией. Диссипируемую энергию в гидравлике называют гидравлическими потерями.
Расчетную форму уравнения Бернулли для элементарной струйки реальной жидкости можно представить в виде
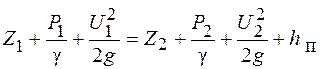 , ,
где hп – гидравлические потери.
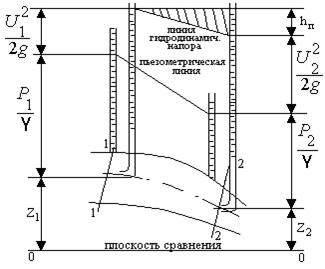 График этого уравнения показан на рисунке 2. График этого уравнения показан на рисунке 2.
Виды движения (течения) жидкости
Течение жидкости вообще может быть неустановившимся (нестационарным) или установившимся (стационарным).
Н  еустановившееся движение– такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения т.е.: еустановившееся движение– такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения т.е.:
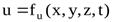 и и 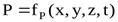 . .
Примером неустановившегося движения может являться вытекание жидкости из опорожняющегося сосуда, при котором уровень жидкости в сосуде постепенно меняется (уменьшается) по мере вытекания жидкости.
У  становившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени не изменяются, т.е. u и P зависят только от координат точки в потоке, но не зависят от момента времени, в который определяются характеристики движения: становившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени не изменяются, т.е. u и P зависят только от координат точки в потоке, но не зависят от момента времени, в который определяются характеристики движения:
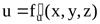 и и 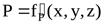 , ,
и, следовательно, 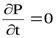 , , 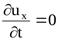 , ,  , , 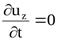 . .
Пример установившегося движения - вытекание жидкости из сосуда с постоянным уровнем, который не меняется (остаётся постоянным) по мере вытекания жидкости.
В случае установившегося течения в процессе движения любая частица, попадая в заданное, относительно твёрдых стенок, место потока, всегда имеет одинаковые параметры движения. Следовательно, каждая частица движется по определённой траектории.
Траекторией называется путь, проходимый данной частицей жидкости в пространстве за определенный промежуток времени.
При установившемся движении форма траекторий не изменяется во время движения. В случае неустановившегося движения величины направления и скорости движения любой частицы жидкости непрерывно изменяются, следовательно, и траектории движения частиц в этом случае также постоянно изменяются во времени.
Поэтому для рассмотрения картины движения, образующейся в каждый момент времени, применяется понятие линии тока.
Линия тока - это кривая, проведенная в движущейся жидкости в данный момент времени так, что в каждой точке векторы скорости ui совпадают с касательными к этой кривой.
Н  ужно различать траекторию и линию тока. Траектория характеризует путь, проходимый одной определенной частицей, а линия тока направление движения в данный момент времени каждой частицы жидкости, лежащей на ней. ужно различать траекторию и линию тока. Траектория характеризует путь, проходимый одной определенной частицей, а линия тока направление движения в данный момент времени каждой частицы жидкости, лежащей на ней.
П  ри установившемся движении линии тока совпадают с траекториями частиц жидкости. При неустановившемся движении они не совпадают, и каждая частица жидкости лишь один момент времени находится на линии тока, которая сама существует лишь в это мгновение. В следующий момент возникают другие линии тока, на которых будут располагаться другие частицы. Еще через мгновение картина опять меняется. ри установившемся движении линии тока совпадают с траекториями частиц жидкости. При неустановившемся движении они не совпадают, и каждая частица жидкости лишь один момент времени находится на линии тока, которая сама существует лишь в это мгновение. В следующий момент возникают другие линии тока, на которых будут располагаться другие частицы. Еще через мгновение картина опять меняется.
Если выделить в движущейся жидкости элементарный замкнутый контур площадью dω и через все точки этого контура провести линии тока, то получится трубчатая поверхность, которую называют трубкой тока. Часть потока, ограниченная поверхностью трубки тока, называется элементарной струйкой жидкости. Таким образом, элементарная струйка жидкости заполняет трубку тока и ограничена линиями тока, проходящими через точки выделенного контура с площадью dω. Если dω устремить к 0, то элементарная струйка превратится в линию тока.
Из приведённых выше определений вытекает, что в любом месте поверхности каждой элементарной струйки (трубки тока) в любой момент времени вектора скоростей направлены по касательной (и, следовательно, нормальные составляющие отсутствуют). Это означает, что ни одна частица жидкости не может проникнуть внутрь струйки или выйти наружу.
При установившемся движении элементарные струйки жидкости обладают рядом свойств:
- площадь поперечного сечения струйки и ее форма с течением времени не изменяются, так как не изменяются линии тока;
- проникновение частиц жидкости через боковую поверхность элементарной струйки не происходит;
- во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малой площади поперечного сечения;
- форма, площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться.
Трубка тока является как бы непроницаемой для частиц жидкости, а элементарная струйка представляет собой элементарный поток жидкости.
При неустановившемся движении форма и местоположение элементарных струек непрерывно изменяются.
Кроме того, установившееся движение подразделяется на равномерное и неравномерное.
Равномерное движение характеризуется тем, что скорости, форма и площадь сечения потока не изменяются по длине потока.
Неравномерное движение отличается изменением скоростей, глубин, площадей сечений потока по длине потока.
Среди неравномерно движущихся потоков следует отметить плавно изменяющиеся движения, характеризующееся тем, что:
- линии тока искривляются мало;
- линии тока почти параллельны, и живое сечение можно считать плоским;
- давления в живом сечении потока зависят от глубины.
28. язкость (внутренние трение) жидкости – свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой.
Основной закон вязкой жидкости был установлен И. Ньютоном (1687 г.) – формула Ньютона
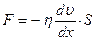
 – сила внутреннего трения; – сила внутреннего трения;
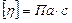 – динамический коэффициент вязкости; – динамический коэффициент вязкости;
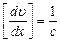 – градиент скорости, показывающий на сколько изменилась скорость при изменении на единицу расстояния в направления ОХ при переходе от слоя к слою (скорость сдвига); – градиент скорости, показывающий на сколько изменилась скорость при изменении на единицу расстояния в направления ОХ при переходе от слоя к слою (скорость сдвига);
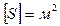 – площадь соприкасающихся слоев. – площадь соприкасающихся слоев.
 крови в норме = 0,004 – 0,005 Па . с. крови в норме = 0,004 – 0,005 Па . с.
Наряду с динамическим коэффициентом вязкости рассматривают кинематический коэффициент вязкости  ( (  – плотность жидкости). – плотность жидкости).
Жидкости делятся по вязким свойствам на два вида: ньютоновские и неньютоновские.
Ньютоновской называется жидкость, коэффициент вязкости которой зависит только от природы и температуры. Для ньютоновских жидкостей 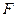 ~ ~ 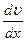 . Для них справедлива формула Ньютона, в которой коэффициент вязкости является постоянным параметром, не зависящим от условий течения жидкости. . Для них справедлива формула Ньютона, в которой коэффициент вязкости является постоянным параметром, не зависящим от условий течения жидкости.
Неньютоновской называется жидкость, коэффициент вязкости которой зависит не только от природы вещества и температуры, но и от условий течения жидкости, в частности, от градиента скорости. Коэффициент вязкости в этом случае не является константой. При этом вязкость жидкости характеризуется условным коэффициентом вязкости, который зависит от определенных условий течения жидкости (например, давления, скорости). Зависимость силы вязкости от градиента скорости становится нелинейной.
Кровь – неньютоновская жидкость. В наибольшей степени это связано с тем, что она обладает внутренней структурой, представляя собой суспензию форменных элементов в растворе – плазме. Плазма – практически ньютоновская жидкость. Поскольку 93% форменных элементов составляют эритроциты, то при упрощенном рассмотрении – кровь – это суспензия эритроцитов в физиологическом растворе. Таким образом, внутренняя структура крови, а следовательно её вязкость, оказывается неодинаковой вдоль кровеносного русла в зависимости от условий течения.
Режимы течения крови разделяют на ламинарное и турбулентное
Ламинарное – это упорядоченное течение жидкости, при котором она перемещается слоями, параллельными направлению течения. При ламинарном течении скорость в сечении трубы изменяется по параболическому закону:
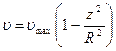 , ,
где  – радиус трубы, – радиус трубы, 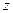 – расстояние от оси, – расстояние от оси, 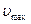 – максимальная скорость. – максимальная скорость.
 С увеличением скорости движения ламинарное течение переходит в турбулентное, при котором происходит интенсивное перемешивание между слоями жидкости, в потоке возникают хаотические движения по сложным траекториям. Для турбулентного течения характерно нерегулярное, беспорядочное изменение скорости со временем в каждой точке потока. С увеличением скорости движения ламинарное течение переходит в турбулентное, при котором происходит интенсивное перемешивание между слоями жидкости, в потоке возникают хаотические движения по сложным траекториям. Для турбулентного течения характерно нерегулярное, беспорядочное изменение скорости со временем в каждой точке потока.
|

