
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
| При решении динамических задач необходимо знать какие силы действуют на тело, закон, позволяющий рассчитать конкретную силу. Цель: получить решение задачи механики исходя из начальных условий, не зная конкретного вида взаимодействия. | ||
| Законы Ньютона в полученной ранее форме не позволяют решать задачи на движение тела с переменной массой и при скоростях, сравнимых со скоростью света. Цель: получить записи законов Ньютона в форме, справедливой для этих условий. | ||
| Импульс силы Векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени. Вектор импульса силы сонаправлен с вектором силы. |  [ I ]= Н.с
[ I ]= Н.с
| |
| Импульс тела. (Количество движения) Векторная физическая величина, являющаяся мерой механического движения и равная произведению массы тела на его скорость. Вектор импульса тела сонаправлен с вектором скорости тела. |  [ p ]= кг м/с
[ p ]= кг м/с
| |
| Импульс силы равен изменению импульса тела. Вектора импульса силы и изменения импульса тела сонаправлены. | 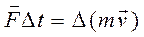
| |
|
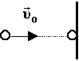
Неупругий удар (шарик "прилипает" к стенке):
| 
| |
| Абсолютно упругий удар (шарик отскакивает с прежней по величине скоростью):
| 
| |
|
Закон сохранения импульса.
| 
| |
|
| 
| |
|
| ||
|
| 
| |
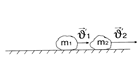
| Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной. | ||
| Замкнутой называется система тел, взаимодействующих только друг с другом и не взаимодействующих с другими телами. Можно пользоваться и для незамкнутых систем, если сумма внешних сил, действующих на тела системы, равна нулю, или процесс происходит очень быстро, когда внешними воздействиями можно пренебречь (взрыв, атомные процессы). | ||
| В общем виде: т.к. система замкнутая, то | 
| |
| Примеры применения закона сохранения импульса: 1. Любые столкновения тел (биллиардных шаров, автомобилей, элементарных частиц и т.д.); 2. Движение воздушного шарика при выходе из него воздуха; 3. Разрывы тел, выстрелы и т.д. | ||
|
Реактивное движение. Под реактивным понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела. При этом возникает т.н. реактивная сила, сообщающая телу ускорение. | ||
|
Билет 7 Механическая работа (А) | ||
|
Единицы работы. | ||
| В международной системе единиц (СИ): [А] = Дж = Н • м Механическая работа равна одному джоулю, если под действием силы в 1 Н оно перемещается на 1 м в направлении действия этой силы. | 1Дж = 1Н • 1м | |
|
Мощность | ||
| Мощность - физическая величина, характеризующая скорость совершения работы и численно равная отношению работы к интервалу времени, за который эта работа совершена. Мощность показывает, какая работа совершается за единицу времени. | 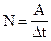
| |
|
| ||
|
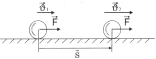
Единицы мощности В международной системе единиц (СИ): Кинетическая энергия. Кинетическая энергия - энергия движущегося тела.(От греческого слова kinema - движение). По определению кинетическая энергия покоящегося в данной системе отсчета тела обращается в ноль. | ||
|
| 
| |
|
| 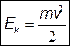
| |
|
| [Ek]=Дж. | |
| Кинетическая энергия - величина относительная, зависящая от выбора СО, т.к. скорость тела зависит от выбора СО. | ||
| Т.о. | 
| |
| Эта теорема справедлива для любого движения и для сил любой природы. Если тело разгоняется из состояния покоя, то Ek1=0. Тогда A = Ek2. Следовательно, кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости. | ||
| Вывод: Работа силы равна изменению кинетической энергии тела, т.е. A = D Ek. Причем, A>0, если Ek увеличивается, и А<0, если Ek<0. | A = D Ek | |
|
Потенциальная энергия. Потенциальная энергия - энергия взаимодействия тел или частей тела. Потенциальная энергия (от латинского potentia - возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними. | ||
|
Диссипативные силы Диссипативными (рассеивающими) наз. силы, работа которых зависит от траектории и по замкнутой траектории не равна нулю (такие силы зависят от скорости). Пример: сила трения. | ||
| § 1.38. Закон сохранения механической энергии. |
| |
| Сумма кинетической и потенциальной энергий системы тел называется полной механической энергией системы. | E = Ep + Ek. | |
| Учитывая, что при совершении работы A = DEk и, одновременно, A = - DEp, получим: DEk = - DEp или D(Ek + Ep)=0 - изменение суммы кинетической и потенциальной энергий (т.е. изменение полной механической энергии) системы равно нулю. | DEk = - DEp | |
| Значит, полная энергия системы остается постоянной: E = Ep + Ek = const. В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется. (Или: полная механическая энергия системы тел, взаимодействующих силами упругости и гравитации, остается неизменной при любых взаимодействиях внутри этой системы). | E = Ep + Ek = const. | |
Например, для тела, движущегося под действием силы тяжести (падение; тело, брошенное под углом к горизонту, вертикально вверх или движущееся по наклонной плоскости без трения):  . .
|
| |
| § 1.39 . Работа силы трения и механическая энергия. |
| |
| Если в системе действуют силы трения (сопротивления), которые не являются консервативными, то энергия не сохраняется. При этом E 1 - E 2 = A тр. Т.е. изменение полной механической энергии системы тел равно работе сил трения (сопротивления) в этой системе. Энергия изменяется, расходуется, поэтому такие силы наз. диссипативными (диссипация - рассеяние). | E1 - E2 = A тр. | |
| Т.о. механическая энергия может превращаться в другие виды энергии, напр., во внутреннюю (деформация взаимодействующих тел, нагревание). | ||
| · | ||
| · | ||
Импульс. Закон сохранения импульса.
При решении динамических задач необходимо знать какие силы действуют на тело, закон, позволяющий рассчитать конкретную силу. Цель: получить решение задачи механики исходя из начальных условий, не зная конкретного вида взаимодействия.
Законы Ньютона в полученной ранее форме не позволяют решать задачи на движение тела с переменной массой и при скоростях, сравнимых со скоростью света. Цель: получить записи законов Ньютона в форме, справедливой для этих условий.
Импульс силы Векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени.  - импульс силы
- импульс силы 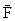 за малый промежуток времени t.
за малый промежуток времени t.
Вектор импульса силы сонаправлен с вектором силы.
 [ I ]= Н.с
[ I ]= Н.с
Импульс тела. (Количество движения) Векторная физическая величина, являющаяся мерой механического движения и равная произведению массы тела на его скорость.
Вектор импульса тела сонаправлен с вектором скорости тела.
 [ p ]= кг м/с
[ p ]= кг м/с
Импульс силы равен изменению импульса тела. Вектора импульса силы и изменения импульса тела сонаправлены.
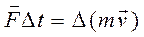
Неупругий удар (шарик "прилипает" к стенке):


Абсолютно упругий удар (шарик отскакивает с прежней по величине скоростью):

Последнее изменение этой страницы: 2019-04-21; Просмотров: 236; Нарушение авторского права страницы