Теория симплекс метода и его приложения

Общая задача линейного программирования состоит в том, чтобы найти неотрицательное значение n при переменных xi удовлетворяющих m линейным ограничениям вида

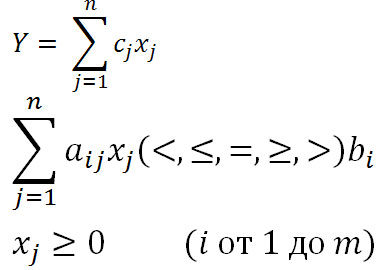
Ранг матрицы r(A) - это максимальное число линейно независимых строк или столбцов матрицы А.
Расширенная матрица системы А*х=b это A_b=(A, b). Система уравнений называют однородной, если вектор b = 0.
Решение x = 0 всегда является решением системы уравнений A*x=0, такое решение называется тривиальным.
Для того, чтобы существовали нетривиальные решения системы, необходимо и достаточно, чтобы r(A)b)=m. Из матрицы А выберем подматрицу порядка m и обозначим ее через В. Пусть X_r - это вектор, который содержит все остальные переменные.
X_b - это вектор, который содержит все переменные, входящие в матрицу В, т.е. соответствуют столбцам матрицы В. Через X_r - это все оставшиеся переменные, а через R обозначим матрицу состоящую из столбцов матрицы А соответствующих переменным X_r. Тогда для произвольного вектора X_r решение системы можно получить, если считать X_b=B^-1*b-B^-1*R*X_r, решения, когда X_r=0, а X_b=B^-1*b наз базисным решением. Базисное решение содержит не более m отличных от 0 переменных. Переменные, вошедшие в вектор X_bназываются базисными переменными, остальные называются небазисными. Базисное решение называется вырожденным, если одна или более базисных переменных =0. Максимальное кол-во базисных решений для системы A*x=b равно

что соответствует числу различных комбинаций из m столбцов матрицы А, которые могут быть выбраны для получения матрицы В. Для некоторых таких комбинаций базисное решение может не существовать, т.к. входящие в данную комбинацию векторы могут оказаться линейно независимыми. Предположим, что все ограничения перенумеруем, что первыми записаны ограничения со знаком ≤, вторые со ≤ и третьими со знаком =.
- Если ограничения имеют знак ≤, то вводим вспомогательную (дополнительную) переменную X_n+i, полагая, что

Для любых переменных X_j (j от 1 до n), удовлетворяющих исходному ограничению X_n+i≥ 0.
- Если i-ое ограничение имеет знак ≥ то необходимо ввести новую вспомогательную (избыточную) переменную X_n+i следующим образом.

Для любых X_j, удовлетворяющих ограничениям.
В результате проделанных операций от исходных ограничений мы переходим к системе из m линейных уравнений с N неизвестными вида A*x=b, при этом n ≤ N ≤ n+m.

Число вновь введенных переменных равно N-n, при этом столбцы А называются производственными векторами. Произвенный вектор соответствующий вспомогательной переменной равен, либо единичному вектору, либо единичному вектору, умноженному на (-1).
Между неотрицательными векторами, соответствующими исходным ограничениям и решениям системы A*x=b существует взаимнооднозначное соответствие. Таким образом добавлением вспомогательных переменных любую задачу линейного программирования можно свести к эквивалентной задаче вида: найти max или min целевой функции y=c*x, где c=(c1, …cn) при условиях A*x=b, x≥ 0. Любое число переменных в задаче линейного программирования принято обозначать через n. Любой вектор Х удовлетворяющий условиям A*x=b и x≥ 0 называют допустимым решением.
Пусть исходная задача приведена к стандартному виду. Тогда:
а) если задача имеет оптимальное решение, то существует по крайней мере 1 базовое оптимальное решение.
б) если имеется допустимое базовое решение, но не оптимальное решение, то через конечное число шагов от этого решения можно перейти к базовому оптимальному решению или установить, что целевая функция (ЦФ) неограничена на множестве всех допустимых решений. При этом на каждом шаге выполняется замена только 1 базисной переменной. Предположим, что ранг матрицы A равен рангу рассматриваемой матрицы и равен m.

Пусть В - это матрица, состоящая из m линейнонезависимых
столбцов матрицы А. Соответствующие и базисные, необязательно оптимальные решения могут быть записаны

все небазисные переменные равны 0. Значение целевой функкции:

Пусть Pj - некоторый произвольный вектор. Найдём вектор

y_j - это вектор, который содержит соответствующие коэффициенты матрицы ограничений после того как все базисные переменные выражены через небазисные.
y_j - меняется на каждой итерации.
c_j - коэффициенты целевой функции, соответствующие i-ой переменной или произвольному вектору P_j.

Теперь предположим, что мы имеем базисное допустимое решение X_b, имеем y_j, Y_j, вычисленных для всех произвольным вектором P_j.
Тогда существуют возможности:
а) разность Y_j - c_j ≥ 0, (j от 1до n). В этом случае базисное допустимое решение оптимально.
б) Y_j-c_j< 0, y_ij ≤ 0, (i от 1 до m). Целевая функция не ограничена, оптимального решения получить нельзя.
с) Y_j-c_j< 0, и для каждого такого j по крайней мере 1 значение y_ij> 0, (i от 1 до m) существует другое базисное допустимое решение, которой соответствует значение ЦФ не меньше, чем значение ЦФ для исходного решения. Если исхоноеое решение не вырожденное, то значение ЦФ можно увеличить заменив в матрице В один вектор.
Симплекс метод исходит из допустимого базисного решения и на каждой итерации производит замену одного вектора в базисе.
Правило замены векторов в базисе:
1) Определение вектора вводимого в базис, так называемое условие оптимальности. Для небазовых переменных вычисляем разность
Y_j-C_k=min_j(Y_j-c_j), Y_j - c_j< 0. Это означает выбор максимального коэффициента в строке y. Вектор P_к соответствующий этому минимуму на следующей итерации вводится в базис. Если вычисляемый минимум достигается при нескольких векторах, то в базис вводится вектор с наименьшим индексом j.
2) Определение вектора исключенного из базиса, так называемое условие допустимости. Вычислеям отношение:

Из базиса исключаетсяся r-й столбец матрицы В и заменяется вектором P_к. В случае неоднозначности выбирается вектор, для которого y_ik имеет наименьшее значение. Если и этим однозначность не исключается, то среди оставшихся векторов выбираем вектор с наименьшим индексом i. Новые значения обозозначим так:

Пусть X_B=y₀; Y_j - c_j=y_n+1; Y=y_{n+1, 0}. Тогда

Рассмотрим задачу нахождения исходногого базисного решения:
Если матица А содержит в качестве подматрицы единичную матрицу. Тогда базовое допустимое решение получается легко:

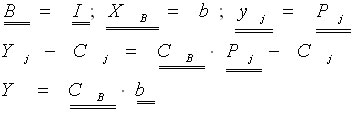
Если единичная матрица не содержится в матрице А, то присоединим к матрице А такую подматрицу (единичную).
Дополнительные векторы называют исскуственными векторами, а соответствующие переменные - исскуственными переменними. Обозначим эти пременные X_ai.
После этого решения можно осуществлять двумя путями:
а) образование искуственной целевой функции и решение задачи в 2 этапа.
б) использование метода введения штрафов (М-метода).
Для получения допустимого решения исходной задачи значение искуственных переменных нужно уменьшить до 0. Для этого коэффициенты ЦФ соответствующие искуственным переменным полагают = “-М”, где М-это большое по значению положительное число. При ручном счёте конкретное значение М не задаётся.
Если исходная задача имеет допустимое решение, то значение искуственных пременных могут быть сделаны равными 0. Если матрица А не содержит ни одного единичного вектора, то вводят искуственные переменные и решают следующую задачу линейного программирования.

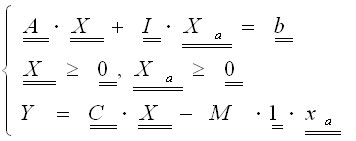
X_a - вектор столбец вида X_a=[X_a1…X_an], I - вектор строка = (1, 1…1).
Начальные базисные допустимые решения для задачи:

Если матрица А содержит единичный вектор e_k, то искуственный вектор e_k вводить не нужно.

Общий вид симплекс таблицы:

БП	СB	b	P1	…	Pn
XB1	СB1	XB1=y0	y11	…	y1n
…	...	…	…	…	…
XBm	СBm	XBm=ym0	ym1	…	ymn
		Y= ym+1, 0	Y1-C1= ym+1, 1		Yn-Cn= ym+1, n

Имеется ряд упрощенных вариантов реализации симплекс метода на ЭВМ. Наиболее распранен метод на правиле выбора переменной вводимой в базис. В общем случае из теории симплекс метода следует, что оптимальное решение задачи линейного программирования всегда соответствует некоторому допустимому базисному решению.
Однако в 2-х случаях это правило не выполняется:
1) если линия постоянных значений целевой функции при оптимальном решении оказывается параллельной линии одного из ограничений, то существует бесконечное множество альтернативных оптимальных решений. При реализации симплекс метода эта ситуация соотвует случаю, когда все разности Y_j - c_j для всех небазисных X_j удовлетворяет условию оптимальности, и по крайней мере 1 разность Y_j - c_j=0. Если вектор связанный с этой разностью можно включить в базис, то существует альтернативное базисное оптимальное решение.
2) Для этого случая характерна ситуация, при которой условие оптимальности показывает, что некоторый базис, будучи введенный в базис улучшит решение, однако, такой вектор сделать базисным нельзя, т. е. если

то P_j не может дать допустимое базисное решение. Такое решение называют, неограниченным. Поскольку переменная X_j ассоциирует с произвольным вектором P_jможно увеличивать неограниченно, не влияя на допустимость решения. Хотя теоретическая основа симплекс метода гарантирует сходимость к оптимальному решению за конечное число шагов, в этом методе не учитывается сложности вычислительного характера, связанные с ошибками округления. Во многом такие ошибки затрудняют применение М-метода (штрафы), поскольку использование «больших штрафов» связано с необходимостью сравнения очень больших и относительно малых чисел. Указанная опасность снижается при разбиении всего процесса задачи на 2 этапа.
Возможность ошибки в округлении не исчезает и при фазовом решении задачи, это связано с тем, что преобразование симплекс таблицы на каждой итерации, основанной на методе исключения переменных Гаусса-Жордана, что приводит к накоплению и распространению ошибок округления в такой степени, что они искажают исходные данные задачи.
Пример с определением условия допуст-ти:

Пусть (X_B )_i =0, а
(B^-1*P_j)_i =0 - это соотв-ий i-ый коэф-т огран-я, кот. ассоц. с вводимым вектором P_j. Предположим, что в результате ошибок окр-ия мы получим (X_B )_i =10_-9, а (B^-1*P_j)_i =10^-6, теперь вектор P_j в решении м. вводить и возникает неверное решение.
С целью уменьшения ошибок окр-ия был разработан модифицированный симплекс метод. Основные шаги этого метода такие же, что и для симплекс метода, отличие - при получении последовательных таблиц на каждой итерации не используется метод Гаусса-Жордана. Основные вычисления связаны с обращением базиса B^-1. Следовательно, в вычислительных процедурах стараются минимизировать ошибки округления, в основном для матрицы B^-1. Помимо контроля за ошибкой округления модифицированный симплекс метод позволяет так же уменьшить и время расчета, при этом время вычислени для модифицированного симплекс метода тем меньше, чем меньше плотность матрицы А (т.е. это отношение числа ненулевых элементов к общему числу элементов) и чем меньше отношение числа ограничений к числу переменных.

Алгоритм симплекс-метода

Теперь мы в состоянии сформулировать алгоритм симплекс-метода для решения задач линейного программирования, заданных в канонической форме. Обычно он реализуется в виде так называемой симплекс-таблицы, изображенной на следующей странице.

В первом столбце этой таблицы располагаются обозначения векторов, входящих в базис.

Второй столбец - коэффициенты 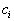целевой функции, соответствующие векторам, входящим в базис.

Третий столбец - компоненты опорного плана. В дополнительной строке в этом столбце пишется величина . Её легко вычислить перемножая числа из второго столбца и третьего столбца и складывая их.

Далее идут столбцы, соответствующие всем векторам , и в этих столбцах записываются координаты этих векторов в рассматриваемом базисе. Заметим, что для векторов, входящих в базис, эти координаты имеют вид (0, 0, ..., 0, 1, 0, ..., 0), где единица стоит в той строке, где находится сам этот базисный вектор.

В дополнительной строке сверху обычно выписывают коэффициенты 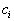, соответствующие этим векторам.

В дополнительной строке снизу пишутся величины 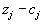, вычисляемые по формулам:

.

Заметим, что для векторов, входящих в базис, эти разности всегда равны нулю.

Далее идут следующие этапы, связанные с преобразованием этой таблицы. При ручном счете каждый раз эту таблицу лучше переписывать заново, при счете на ЭВМ (который, естественно, всегда используется при решении практических, а не учебных задач), эта таблица просто преобразуется в памяти ЭВМ.

Этап 1

Просматривается дополнительная строка снизу, где записаны разности.

Если все эти разности ,

то план является оптимальным

Этап 2

Если есть столбцы, где , то выбирается столбец с максимальным значением этой разности. Индекс j определит вектор, вводимый в базис.

Пусть , то есть в базис надо вводить вектор . Назовем столбец, соответствующий этому вектору, направляющим столбцом. В дальнейшем мы будем направляющий столбец помечать символом .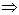

Этап 3

Просматривается столбец, соответствующий этому вектору. Если все , то значения целевой функции неограничены снизу. Если есть 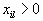, то находятся

где просматриваются лишь те дроби ,

для которых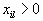

Пусть этот минимум достигается для вектора . Тогда именно вектор подлежит выводу из базиса. Строка, соответствующая этому вектору, называется направляющей строкой. В дальнейшем в примерах мы будем

помечать ее символом .

Этап 4

После того, как определены направляющие столбец и строка, начинает заполняться новая симплекс-таблица, в которой на месте направляющей

строки будет стоять вектор .

Обычно заполнение этой новой таблицы начинается именно с направляющей строки. В качестве компоненты опорного плана туда

пишется величина , то есть

.

Остальные элементы этой строки заполняются величинами

.

Обратите внимание на особую роль элемента , стоящего на пересечении направляющей строки и направляющего столбца. Именно на него делятся все бывшие элементы направляющей строки. На месте бывшего элемента автоматически появляется единица.

Написанные выше формулы для пересчета элементов направляющей строки можно записать следующим правилом:

.

Этап 5

Далее начинается пересчет всех остальных строк таблицы, включая и дополнительную нижнюю строку по формулам: для компонент плана

;

для координат разложения по базису

;

для дополнительной строки

.

Обратите внимание на то, что все эти формулы по сути дела строятся по одному правилу

.

Это правило применимо и к компонентам плана, и к величинам 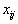, и к разностям 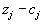. Его даже можно использовать для пересчета элементов самого направляющего столбца, хотя проще заполнить его нулями, оставив

1 на месте бывшего элемента .

Далее итерации продолжаются.

Пример

Решить задачу линейного программирования

В данном случае вектор равен (0, 1, -3, 0, 2, 0), а в векторной форме ограничения могут быть записаны в виде

.

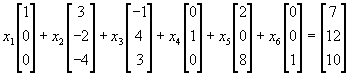Заполним исходную симплекс-таблицу, взяв в качестве исходного базиса

вектора ,

что удобно из-за их вида.

Исходная симплекс-таблица

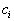
	Ба-		План	0	1	-3	0	2	0
	зис
		0	7	1	3	-1	0	2	0
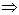
		0	12	0	-2	4	1	0	0
		0	10	0	-4	3	0	8	1
			0	0	-1	3	0	-2	0

Обратите внимание на то, что из-за специфического вида векторов 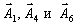в столбец " план" просто переписался вектор 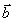, а в качестве координат векторов в нашем базисе стоят просто сами векторы.

Ну, а величины приходится считать:

Первая итерация

Просматривая дополнительную строку мы видим, что в ней всего один положительный элемент - в столбце, соответствующем вектору . Следовательно, этот вектор надо вводить в базис и этот столбец и будет направляющим столбцом.

В этом направляющем столбце есть два положительных числа - 4 и 3. Поэтому нужно рассмотреть два частных

и выбрать из них наименьшее. Так как

и он достигается на векторе , то этот вектор подлежит выводу из базиса и соответствующая ему строка и будет направляющей строкой.

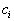
	Ба-		План	0	1	-3	0	2	0
	зис
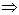
		0	10	1		0		2	0
		-3	3	0		1		0	0
		0	1	0		0		8	1
			-9	0		0		-2	0

Заполним теперь новую симплекс-таблицу, следуя сформулированным выше правилам.

Начинается заполнение, естественно, со второй строки (так как она была направляющей), а затем пересчитываются все остальные строки.

Вторая итерация

Просматривая дополнительную строку мы вновь видим в ней всего один положительный элемент это 1/2, стоящая в столбце вектора . Следовательно, этот вектор надо ввести в базис и этот столбец будет направляющим.

В столбце, соответствующем вектору , всего один положительный элемент это 5/2, которая стоит в первой строке. Поэтому первая строка будет

направляющей и вектор

должен быть выведен из базиса.

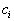
	Ба-		План	0	1	-3	0	2	0
	зис
		1	4		1	0			0
		-3	5		0	1			0
		0		1	0	0		10	1
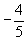
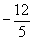
			-11		0	0			0

Запишем новую симплекс-таблицу, следуя сформулированным выше правилам.

В получившейся таблице в дополнительной строке стоят лишь отрицательные числа и нули. Поэтому получившийся план является оптимальным.

Итак, оптимальный план имеет вид

то есть , а все остальные Ему соответствует значение целевой функции, равное -11.

8. Симплексный метод (назначение метода, симплексные таблицы, правила построения симплекс- таблиц, понятие индексной строки, разрешающего элемента, правило прямоугольника).

Назначение метода

В общем виде, когда в задаче участвуют N -неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n -мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.

Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число " шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).

Симплексные таблицы

Приведя ЗЛП к предпочтительному виду, её заносят в симплексную таблицу.

max Z = 18x1 + 20x2 + 32x3

18x1 + 15x2 +12x3 + x4 = 720;

6x1 + 4x2 + 8x3 + x5 =384;

5x1 + 3x2 + 12x3 + x6 = 360;

Базисные переменные	Коэффициенты	A0	X1	X2	X3	X4	X5	X6
			18	20	32	0	0	0
X4	0	720	18	15	12	1	0	0
X5	0	384	6	4	8	0	1	0
X6	0	360	5	3	12	0	0	1
Zj - Cj		0	-18	-20	-32	0	0	0

 

∆ ₀ = 0*720 + 0* 384 + 0* 360 = 0; ∆ ₀ = Z(x₀)

∆ _I = ∑ коэфф. * a_ij - c­_j;

∆ ₁ = 0*18 + 0*6+ 0*5 – 18= -18

Правило прямоугольника

Чтобы найти элемент новой симплексной таблицы, нужно воспользоваться правилом прямоугольника. Для этого в исходной таблице выделяют прямоугольник, вершинами которого служат нужные для вычисления элементы. Диагональ, содержащую разрешающий и искомый элементы новой таблицы, называют главной, а другую – побочной. Чтобы получить элемент новой симплексной таблицы, нужно из произведения угловых элементов главной диагонали вычесть произведение угловых элементов побочной диагонали и полученное число разделить на разрешающий элемент, выделенный рамкой.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: