Циркуляция вектора по бесконечно малому контуру.

Проведем в векторном поле замкнутую кривую и примем для нее определенное направление обхода. Затем разобьем ее на малые дуги. Хорды, стягивающие эти элементы кривой, имеют направления, совпадающие с направлением обхода.Обозначим их . В произвольной точке i –того участка кривой возьмем вектор поля и составим сумму

(2.37)

После этого устремим к нулю. Если при этом предел суммы (2.37) существует и не зависит от способа разбиения кривой и выбора точек определения векторов , то мы приходим к криволинейному интегралу

(2.38)

Криволинейный интеграл (2.38) называется циркуляцией векторного поля по замкнутому контуруL.Если, например, - это силовое поле, то физический смысл циркуляции состоит в том, что она выражает работу поля по пути L. Будем стягивать контур, по которому вычисляется циркуляция, к точке. Это позволит определить новую локальную характеристику отличную от дивергенции. Отличие заключается в частности в том, что ее значение будет в общем случае зависеть не только от точки, к которой стягивается контур, но и от его ориен­тации в пространстве. Поэтому можно предположить, что инте­ресующеенас предельное значение циркуляции, которая сама по себе есть скаляр, выражается через скалярноепроизведение некоего вектора (его предстоим нам найти) и единичного вектора нормали к плоскости контура, стягиваемого к точке.Возьмем в поле замкнутый контур L, натянем на него произвольную поверхность S и определим на ней направление внешней нормали. Построим на ее малом участке, который в пределе можно считать плоским, прямоугольник. Его стороны обозначим и , причем . Площадь этого прямоугольника

(2.39)

, а вектор единичной нормали

(2.40)

Вычислим циркуляцию вектора вдоль контура прямоугольника. С учетом последующего перехода к пределу она равна

(2.41)

, где означает бесконечно малую более высокого порядка, чем .

Разделим правую и левую части (2.41) на и перейдем к пределу. Тогда с учетом того, что в левой части стоит выражение для циркуляции вдоль бесконечно малого контура, получим

(2.42)

Проекция 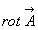на направление равна пределу отношения циркуляции вектора вдоль замкнутого контура, проведенного в плоскости, перпендикулярной , к площади, ограни­ченной этим контуром, при стягивании его к точке. Рассмотрим теперь всю совокупность элементарных площадок, на которые с помощью прямоугольников, подобных только что рассмотренному, можно разбить поверхность S. Применим к каждой из них соотношение (2.41), просуммируем и перейдем к пределам, как это было сделано при выводе (2.42). Сумма правых частей
приведет нас к потоку через поверхность S.
Сумма левых частей сведется к циркуляции векторного поля по контуру L, так как общие части границ соседних элементарных площадок проходятся в противоположном направлении и при суммировании циркуляции их вклады компенсируют друг друга. Из сказанного следует

ТЕОРЕМА. Поток вихря 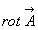через поверхность S ,.натянутую на замкнутый контур L , равен циркуляции векторного поля по этому контуру, если компоненты поля вместе с их частными произ­водными непрерывны на S и L .

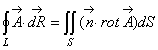(2.43)

⇐ Предыдущая33343536373839404142Следующая ⇒

Поделиться: