Решение обыкновенных дифференциальных уравнений. Задача Коши

Стр 1 из 3Следующая ⇒

Н.Г Бикбулатова

ИНФОРМАТИКА

Методические указания по выполнению курсовой работы на тему: «Визуализация численных методов.

Решение обыкновенных дифференциальных уравнений»

для студентов очной формы обучения

на базе среднего (полного) общего образования направления

11.03.01 «Радиотехника»

(профиль «Аудиовизуальная техника»)

программа академического бакалавриата

в соответствии с требованиями ФГОС ВО 3 +

Екатеринбург

2016

ББК 22.19

УДК 517.9

Рецензент: профессор кафедры ИСТ Л.И. Долинер

Бикбулатова Н.Г

Информатика: методические указания для курсовой работы / Бикбулатова Н.Г — Екатеринбург: УрТИСИ СибГУТИ, 2016. — 29 с.

Методические указания рекомендованы для выполнения курсовой работы по теме: «Визуализация численных методов. Решение обыкновенных дифференциальных уравнений» по дисциплине «Информатика» для студентов очной формы обучения на базе среднего (полного) общего образования направления 11.03.01 «Радиотехника» (профиль «Аудиовизуальная техника»)

в соответствии с требованиями ФГОС ВО 3 +.

Рекомендовано НМС УрТИСИ «СибГУТИ» в качестве методических указаний по выполнению курсовой работы для студентов очной формы обучения на базе среднего (полного) общего образования направления 11.03.01 «Радиотехника» (профиль «Аудиовизуальная техника») в соответствии с требованиями ФГОС ВО 3 +.

ББК 22.19

УДК 517.9

Кафедра информационных систем и технологий

Ó УрТИСИ «СибГУТИ», 2016

Содержание

Введение. 4

Методические рекомендации по выполнению курсовой работы.. 5

Построение графиков функций в среде Visual Basic. 16

Задание к курсовой работе. 24

Литература. 25

Приложение 1. 26

Приложение 2. 27

Введение

Данное пособие создавалось с целью оказать помощь студентам в подготовке и написании курсовой работы. Курсовая работа завершает изучение курса «Информатика» связанного с применением компьютеров в профессиональной деятельности, к которой готовятся студенты. В этой работе студенты должны показать свои умения применять основные численные методы для решения дифференциальных уравнений 1-го порядка, грамотного распределения информации и использования возможностей среды программирования Visual Basic.

В пособии рассматриваются следующие вопросы: цель курсовой работы и примерное календарное планирование по ее выполнению, структура работы и отчета по курсовой работе, основные этапы решения инженерных задач на ЭВМ, основы построения математических моделей, задания для выполнения в качестве курсовой работы для студентов направления 11.03.01 «Радиотехника» (профиль «Аудиовизуальная техника»).

Методические рекомендации будут полезны не только студентам, выполняющим курсовую работу, но и студентам, изучающим курсы «Вычислительная математика» и «Численные методы», а так же желающим освоить тему и построение графиков функций в среде Visual Basic.

Методические рекомендации по выполнению курсовой работы

Назначение курсовой работы

Курсовая работа является важнейшей составляющей курса и первой объёмной самостоятельной инженерно-расчётной работой студента. Курсовая работа завершает подготовку по дисциплине «Информатика» и становится базой для выполнения последующих курсовых проектов по специальным дисциплинам.

Темой курсового проекта является «Визуализация численных методов. Решение обыкновенных дифференциальных уравнений» путём:

1) составление и отладка программы на языке Visual Basic;

2) проверки решения с помощью приложения MathCad.

В ходе выполнения курсовой работы предполагается изучение теоретического материала по одной из предложенных тем и выполнение практического задания средствами VBA и MathCad для решения дифференциального уравнения предложенными численными методами.

2. Примерное содержание пояснительной записки

Пояснительная записка оформляется на листах формата А4.

Первая страница – титульный лист, оформленный по общим правилам. Описание работы должно включать два раздела:

1) Теоретический материал (Приложение 1);

2) Практическое решение задачи (Приложение 2):

· постановку задачи и математическую модель,

· описание используемых методов (применительно к конкретной задаче),

· блок-схемы основных процедур,

· виды формы проекта (исходный – для ввода данных, итоговый – с представленным решением и графиком),

· листинг программы на языке Visual Basic,

· решение задачи в MathCad,

· вывод по работе.

3. Календарный план выполнения работы

На выполнение курсовой работы отводится 7 недель (7 практических занятий). На занятии предполагается отчет по самостоятельной работе студента и обсуждение хода работы с преподавателем.

Неделя.	Содержание выполняемой работы	Кол-во часов
1	Построение математической модели задачи. Решение задачи в MathCad.	2
2	Описание численных методов решения задачи. Построение алгоритма решения задачи для заданных численных методов в виде блок-схемы.	2
3	Написание программы решения задачи на языке программирования VisualBasic.	2
4	Отладка программы на компьютере.	2
5	Пояснительная записка сдается на проверку.	2
6	Защита курсовой работы.	2
7	Защита курсовой работы.	2
ИТОГО		14

Постановка задачи

Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если эти дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши. Часто в задаче Коши в роли независимой переменной выступает время.

Задачу Коши можно сформулировать следующим образом.

Пусть дано дифференциальное уравнение и начальное условие y ( x ₀ ) = y ₀. Требуется найти функцию y ( x ), удовлетворяющую как указанному уравнению, так и начальному условию.

Численное решение задачи Коши сводится к табулированию искомой функции.

График решения дифференциального уравнения называется интегральной кривой.

Геометрический смысл задачи:

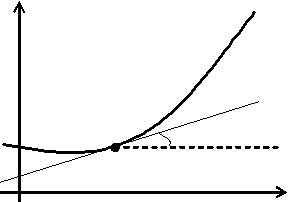
- тангенс угла наклона касательной к графику решения в точке ( x, y ) к оси ОХ, - угловой коэффициент (рис.1).

а tg(α ) = f(x, y)

Существование решения:

Если правая часть f ( x, y ) непрерывна в некоторой области R, определяемой неравенствами

|x – x ₀| < a; |y – y ₀| < b

то существует, по меньшей мере, одно решение y = y ( x ), определённое в окрестности |x – x ₀| < h, где h – положительное число.

Это решение единственно, если в R выполнено условие Липшица

где N – некоторая постоянная (константа Липшица), зависящая, в общем случае, от a и b. Если f ( x, y )имеет ограниченную производную в R, то можно положить

N = max| | при .

Метод Эйлера

Иногда этот метод называют методом Рунге-Кутта первого порядка точности. Данный метод одношаговый. Табулирование функции происходит поочередно в каждой точке. Для расчета значения функции в очередном узле необходимо использовать значение функции в одном предыдущем узле.

Пусть дано дифференциальное уравнение первого порядка

с начальным условием

y ( x ₀ ) = y ₀.

Выберем шаг h и введём обозначения:

x_i = x ₀ + i ^. h и y_i = y ( x_i ), ,

где i = 0, 1, 2, …

x_i – узлы сетки,

y_i- значение интегральной функции в узлах.

Иллюстрации к решению приведены на рисунке 2.

Проведем прямую АВ через точку (x_i, y_i) под углом α. При этом

tgα = f(x_i, y_i) (2) В соответствии с геометрическим смыслом задачи, прямая АВ является касательной к интегральной функции. Произведем замену точки интегральной функции точкой, лежащей на касательной AB.

Тогда y_i₊₁ = y_i+Δ y (3) Из прямоугольного треугольника АВС (4) Приравняем правые части (2) и (4). Получим .

Отсюда

Рисунок 2 - Метод Эйлера

Подставим в это выражение формулу (3), а затем преобразуем его. В результате получаем формулу расчета очередной точки интегральной функции:

(5) Из формулы (5) видно, что для расчета каждой следующей точки интегральной функции необходимо знать значение только одной предыдущей точки. Таким образом, зная начальные условия, можно построить интегральную кривую на заданном промежутке.

Блок-схема процедуры решения дифференциального уравнения методом Эйлера приведена на рисунке 3.

Рисунок 3 - Блок-схема процедуры решения дифференциального уравнения методом Эйлера

Метод Эйлера – один из простейших методов численного решения обыкновенных дифференциальных уравнений. Но существенным его недостатком является большая погрешность вычислений. На рисунке 2 погрешность вычислений для i-го шага обозначена ε. С каждым шагом погрешность вычислений увеличивается.

Задача.

Построить график функции y=sin(x) на отрезке [a, b]. Шаг табулирования принять равным h.

Решение.

Для построения графика функции в среде Visual Basic удобно воспользоваться некоторыми графическими компонентами.

Рисунок 9 - Расположение основных компонентов в окне General

Компонент Picture Box (

) используется в качестве контейнера для построения графика. Он представляет собой матрицу из точек (пикселей), причём имеется возможность управлять цветом каждой отдельной точки. Координаты любой точки определяются парой целых чисел – ее порядковым номером в строке Х и порядковым номером строки внутри объекта Y. Таким образом, координаты левого верхнего угла компонента (0, 0). Число точек в строке и число строк определяются размером компонента.

Рисунок 10 - Координаты объекта PictureBox

На рис. 10 показано расположение осей и координаты угловых точек объекта.

Компонент Line ( ) используется для построения осей и отрезков ломаной графика функции.

Суть построения графика сводится к тому, что функцию необходимо представить в виде таблицы (протабулировать), а затем отметить на шаблоне графика точки и соединить их между собой.

Алгоритм построения графика функции приведен на рисунке 12. Алгоритм может быть модифицирован. В частности, некоторые процедуры могут быть объединены, а порядок действий в некоторых случаях может быть изменен.

Рассмотрим алгоритм более подробно.

До реализации алгоритма необходимо описать подпрограмму- функцию для построения графика. Это необходимо для облегчения модификации программы. Если потребуется построение графика другой функции, достаточно будет только изменить подпрограмму.

Так же до построения графика необходимо создать и отредактировать форму. Пример разработки формы приведен на рисунке 11. На форме надо расположить компоненты для ввода исходных данных, компонент для вывода на печать таблицы, командную кнопку, контейнер для размещения графика (PictureBox). Внутри PictureBox надо нарисовать оси координат с помощью прямых линий и расположить метки для записи границ отрезка значений аргумента функции и экстремумов функции на рассматриваемом отрезке.

Ввод исходных данных осуществляется в рассматриваемой программе при нажатии на командную кнопку. Очень часто ввод данных реализуется с помощью компонента TextBox.

Процедуру табулирования функции удобно осуществлять в цикле с параметром, так как известно количество обсчитываемых точек графика. До выполнения процедуры надо задать количество строк таблицы.

Количество строк рассчитывается по формуле k=n+2, где k – количество строк, а n – количество отрезков табулирования. Число строк должно быть больше количества отрезков на 2, так как необходимо учесть начальную точку (нулевую) и строку для записи заголовков столбцов страницы.

В самой процедуре табулирования можно совместить два действия – табулирование и расчет экстремумов. Такой вариант решения приведен в листинге программы на рисунке13.

Основной сложностью построения графика является переход от математического значения функции и аргумента к экранным координатам, используемым для построения графика. При решении этой проблемы необходимо учитывать противоположное направление осей на математическом графике и на объекте PictureBox и необходимость масштабирования картинки.

Коэффициенты масштабирования графика рассчитываются по следующим формулам:

где kx - коэффициент масштабирования по оси ОХ,

NPX – количество пикселей объекта PictureBox, отводимых для построения графика по горизонтали,

a – начальное значение отрезка аргумента функции,

b – конечное значение отрезка аргумента функции.

где Ky - коэффициент масштабирования по оси ОY,

NPY – количество пикселей объекта PictureBox, отводимых для построения графика по вертикали,

min – минимальное значение функции,

max – максимальное значение функции.

Перевод математических координат текущей точки в экранные производится по формулам:

zx = Round(ox + (x(i) - a) * kx),

zy = Round(oy - (y(i) - Min) * ky),

где zx, zy – экранные координаты текущей точки,

ox, oy - координаты точки пересечения осей в компоненте pictureBox,

x(i), y(i) – математические координаты текущей точки,

kx, ky – коэффициенты масштабирования.

В формуле расчета экранной координаты ординаты текущей точки используется знак «минус» для учета противоположного направления осей (на экране и на графике).

Листинг программы построения графика функции приведен на рисунке 13.

Примеры форм с результатами работы программы для различных исходных данных приведены на рисунках 14 и 15.

Рисунок 11 - Пример разработки формы

Рисунок 12 - Алгоритм построения графика функции

Rem Описание переменных

Dim x() As Single, y() As Single

Private a As Single

Private b As Single

Rem Ввод данных

a = Val(Text1.Text)

b = Val(Text2.Text)

h = Val(Text3.Text)

Rem очистка картинки

Picture1.Cls

Задание к курсовой работе

Литература

Основная литература

1. Информатика. Базовый курс: учебное пособие для вузов / под ред. С. В. Симоновича.- 3-е изд.- СПб.: Питер, 2012. – (Стандарт третьего поколения)

2. Информатика. Базовый курс: учебник для вузов: для бакалавров и специалистов/ под ред. С. В. Симоновича. – 3-е изд. – СПб.: Питер, 2011. - (Стандарт третьего поколения).

3. Макарова Н., Волков В. Информатика: Учебник для вузов. Стандарт третьего поколения. — СПб.: Питер, 2011 г. — 576 с. — Электронное издание. — Гриф УМО Учебник.

4. Шапорев С. Информатика. Теоретический курс и практические занятия. — СПб.: БХВ-Петербург, 2010 г. — 480 с. — Электронное издание. — Гриф НМС по математике.

Дополнительная литература

1. Алексеев А.П. Информатика 2015: учебное пособие. — Москва: СОЛОН-ПРЕСС 2015 г.— 400 с. — Электронное издание.

2. Львович И.Я. Основы информатики [Электронный ресурс]: учебное пособие/ Львович И.Я., Преображенский Ю.П., Ермолова В.В.— Электрон. текстовые данные.— Воронеж: Воронежский институт высоких технологий, 2014.— 339 c.

3. Прохорова О.В. Информатика [Электронный ресурс]: учебник/ Прохорова О.В.— Электрон. текстовые данные.— Самара: Самарский государственный архитектурно-строительный университет, ЭБС АСВ, 2013.— 106 c

4. Калабухова Г.В.Компьютерный практикум по информатике. Офисные технологии: учебное пособие/Г.В. Калабухова.- М.: ФОРУМ: ИНФРА-М, 2013.-336с. - (Высшее образование)

5. Браун С. Visual Basic 6. Учеб. курс. – СПб.: Питер, 2006. – 574 с.

Приложение 1

Темы для теоретического раздела:

1. Информатика как наука. Основные разделы информатики. Взаимосвязь материи, энергии, информации.

2. Понятие информации, ее свойства.

3. Методы получения информации. Типы сигналов. Типы и виды информации.

4. Кодирование информации. Двоичное кодирование.

5. Измерение информации. Алфавитный подход.

6. Измерение информации. Вероятностный подход (при равновероятных и неравно вероятных событиях).

7. Принципы автоматической обработки информации (Принципы фон Неймана).

8. Поколения ЭВМ.

9. Магистрально-модульный принцип устройства компьютера.

10. Системная (материнская) плата.

11. Шины. Назначение, типы, основные характеристики.

12. Микропроцессор. Назначение, типы, основные характеристики.

13. Постоянное запоминающее устройство. Назначение, типы, основные характеристики.

14. Оперативное запоминающее устройство. Назначение, типы, основные характеристики. КЭШ-память.

15. Накопители на гибких магнитных дисках. Назначение, типы, основные характеристики.

16. Накопители на жестких магнитных дисках. Назначение, типы, основные характеристики.

17. Накопители на оптических и магнито-оптических дисках. Назначение, типы, основные характеристики.

18. Программные и аппаратные компоненты Вычислительных сетей (ВС).

19. Требования, предъявляемые к ВС.

20. Классификация ВС.

21. Эталонная модель OSI.

22. Методы передачи данных

23. Методы коммутации

24. Линии связи

25. Основные принципы построения сети Internet

26. Основные протоколы Internet

27. Электронная почта

28. Система World Wide Web

29. IP-телефония

30. Защита информации в Internet

Приложение 2

Таблица 1 - Задания для курсовых работ

№ варианта	Дифференциальные уравнения	X₀	X_k	h	Y₀	Общее решение	Методы решения
1	x× y× dx+(x+1) × dy=0	1.2	2	0.1	1	y=c× (x+1) × exp(-x)	Эйлер, Рунге-Кутт
2	y¢ =x× y ²+2× x× y	0	2	0.2	-1.8	y=-2/(1+c× exp(-x²))	Эйлер, Эйлер модифицированный
3	y¢ =2× × ln(x)	1	2	0.1	16	y=(x× ln(x)-x+c) ²	Рунге-Кутт, Эйлер модифицированный
4	y¢ × ctg(x)=2-y	0	1	0.1	1	y=2-cos(x)	Эйлер, Рунге-Кутт
5	y¢ × x=3× y	1	1.4	0.05	2	y=c× x ³	Эйлер, Эйлер модифицированный
6	yy¢ +x=1	0	1	0.1	2	y=	Рунге-Кутт, Эйлер модифицированный
7	y¢ =-0.05× y	1	2	0.1	2	y=c× exp(-0.05•x)	Эйлер, Рунге-Кутт
8	y¢ =4× x-2× y	1.2	2	0.1	2.4	y=c× exp(-2× x)+2× x-1	Эйлер, Эйлер модифицированный
9	(y²-2x× y)dx+x²dy =0	1	2	0.1	0.2	y=x²/(c+x)	Рунге-Кутт, Эйлер модифицированный
10	(y¢ -y) × x=e ^x	1	2	0.1	4	y=exp(x)(ln\|x\|+c)	Эйлер, Рунге-Кутт
11	y¢ × x=exp(x)-y	1.0	2	0.1	1	y=[exp(x)+1-e]/x	Эйлер, Эйлер модифицированный
12	y¢ × x=4y	1	1.4	0.05	2	y=x⁴× c	Рунге-Кутт, Эйлер модифицированный
13	y¢ × (x+1)=y + 2	0	0.8	0.1	0	y=(x+1) × c-2	Эйлер, Рунге-Кутт
14	2× x× y× dx-(x+1)× dy=0	0	0.8	0.05	4	y=e²^x× c/(x+1)²	Эйлер, Эйлер модифицированный
15	y¢ +2× x× y=x× exp(-x ²)	0	1	0.1	1	y=exp(-x ²)(c+x ²/2)	Рунге-Кутт, Эйлер модифицированный
16	y¢ +y=cos(x)	0	p/2	p/10	1	y=c× exp(-x)+[cos (x)+ +sin (x)] /2	Эйлер, Рунге-Кутт
17	y¢ × x=y+1	1	5	0.5	-0.9	y=c× x-1	Эйлер, Эйлер модифицированный
18	3x² – y¢ =0	1	1.8	0.1	0	y=x³-c	Рунге-Кутт, Эйлер модифицированный
19	x× y¢ +y=y ²× ln(x)	1	1.6	0.1	4	y=[1+ln (x)+c× x]^-1	Эйлер, Рунге-Кутт
20	(1+x ²)× dy+y× dx=0	1	1.8	0.1	1	ln\|y\|=-arctg(x)+c	Эйлер, Эйлер модифицированный
21	y¢ =y/x+sin(y/x)	1	1.5	0.05	p/2	y=2× x× arctg(c× x)	Рунге-Кутт, Эйлер модифицированный
22	x× y¢ -y=x ²× cos(x)	1.8	2.4	0.1	0.5	y=x× [sin(x)+c]	Эйлер, Рунге-Кутт
23	y¢ +y/x=3/x	1	1.8	0.1	0	y=3(x-1)/x	Эйлер, Эйлер модифицированный
24	y¢ =2× x²+2× y	0	1	0.1	1	y=1.5× exp(2× x)-x²-x-c	Рунге-Кутт, Эйлер модифицированный
25	y¢ × sin(x)-y× cos (x)=0	p/2	3p/4	p/20	1	y=sin (x)	Эйлер, Рунге-Кутт
26	(1+y ²) × dx=x× dy	1	1.5	0.05	1	y=tg( ln (c× x) )	Эйлер, Эйлер модифицированный
27	(x-y) × dx+x× dy=0	1.2	2	0.1	2	y=x× (c-ln (x))	Рунге-Кутт, Эйлер модифицированный
28	x× y¢ =y× [ln (y)-ln (x)]	1	2	0.1	1	y=x× exp(1+c× x)	Эйлер, Рунге-Кутт
29	x ²+x× y¢ =y	1	1.4	0.05	0	y=x-x ²	Эйлер, Эйлер модифицированный
30	y¢ +2× x× y=2× x× y ²	1	1.2	0.02	2	y=[(1+c× exp(x ²)]^-1	Рунге-Кутт, Эйлер модифицированный

Public Class Form1

Private x0, y0, xk, h As Single

Private n, m As Integer

Private k1, k2, k3, k4, k As Single

Dim x() As Single

Dim y1() As Single

Dim y2() As Single

Dim o() As Single

Function F(ByVal z As Single, ByVal t As Single) As Single

F = (Math.Exp(z) + t * z) / z

End Function

Function c(ByVal z As Single, ByVal t As Single) As Single

c = (t - Math.Exp(z) * Math.Log(z)) / Math.Exp(z)

End Function

Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click

x0 = Val(TextBox1.Text)

y0 = Val(TextBox2.Text)

xk = Val(TextBox3.Text)

h = Val(TextBox4.Text)

n = (xk - x0) / h

ReDim x(n)

ReDim y1(n)

ReDim y2(n)

ReDim o(n)

y1(0) = y0

y2(0) = y0

DataGridView1.ColumnCount = 4

DataGridView1.RowCount = n + 1

DataGridView1.Columns(0).Name = " x"

DataGridView1.Columns(1).Name = " y"

DataGridView1.Columns(2).Name = " ym"

DataGridView1.Columns(3).Name = " o“

For m As Integer = 0 To n

x(m) = x0 + (m) * h

o(m) = Math.Exp(x(m)) * (Math.Log(x(m)) + c(x0, y0))

DataGridView1.Item(0, m).Value = Str(x(m))

DataGridView1.Item(3, m).Value = Str(o(m))

Next m

For m As Integer = 0 To n - 1

x(m) = x0 + m * h

y1(m + 1) = Math.Round(y1(m) + h * F(x(m), y1(m)), 4)

k1 = h * F(x(m), y2(m))

k2 = h * F(x(m) + (h / 2), y2(m) + (k1 / 2))

k3 = h * F(x(m) + (h / 2), y2(m) + (k2 / 2))

k4 = h * F(x(m) + h, y2(m) + k3)

k = (k1 + 2 * k2 + 2 * k3 + k4) / 6

y2(m + 1) = y2(m) + k

DataGridView1.Item(1, m).Value = Str(y1(m))

DataGridView1.Item(2, m).Value = Str(y2(m))

Next m

For m As Integer = 0 To n - 1

Chart1.Series(" Series1" ).Points.AddXY(x(m + 1), o(m))

Chart1.Series(" Series2" ).Points.AddXY(x(m + 1), y1(m))

Chart1.Series(" Series3" ).Points.AddXY(x(m + 1), y2(m))

Next m

End Sub

Private Sub Chart1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Chart1.Click

End Sub

End Class

Н.Г Бикбулатова

ИНФОРМАТИКА

Методические указания по выполнению курсовой работы на тему: «Визуализация численных методов.

Решение обыкновенных дифференциальных уравнений»

для студентов очной формы обучения

на базе среднего (полного) общего образования направления

11.03.01 «Радиотехника»

(профиль «Аудиовизуальная техника»)

программа академического бакалавриата

в соответствии с требованиями ФГОС ВО 3 +

Екатеринбург

2016

ББК 22.19

УДК 517.9

Рецензент: профессор кафедры ИСТ Л.И. Долинер

Бикбулатова Н.Г

в соответствии с требованиями ФГОС ВО 3 +.

ББК 22.19

УДК 517.9

Кафедра информационных систем и технологий

Ó УрТИСИ «СибГУТИ», 2016

Содержание

Введение. 4

Методические рекомендации по выполнению курсовой работы.. 5

Построение графиков функций в среде Visual Basic. 16

Задание к курсовой работе. 24

Литература. 25

Приложение 1. 26

Приложение 2. 27

Введение

Методические рекомендации по выполнению курсовой работы

Назначение курсовой работы

1) составление и отладка программы на языке Visual Basic;

2) проверки решения с помощью приложения MathCad.

2. Примерное содержание пояснительной записки

Пояснительная записка оформляется на листах формата А4.

1) Теоретический материал (Приложение 1);

2) Практическое решение задачи (Приложение 2):

· постановку задачи и математическую модель,

· описание используемых методов (применительно к конкретной задаче),

· блок-схемы основных процедур,

· виды формы проекта (исходный – для ввода данных, итоговый – с представленным решением и графиком),

· листинг программы на языке Visual Basic,

· решение задачи в MathCad,

· вывод по работе.

3. Календарный план выполнения работы

Неделя.	Содержание выполняемой работы	Кол-во часов
1	Построение математической модели задачи. Решение задачи в MathCad.	2
2	Описание численных методов решения задачи. Построение алгоритма решения задачи для заданных численных методов в виде блок-схемы.	2
3	Написание программы решения задачи на языке программирования VisualBasic.	2
4	Отладка программы на компьютере.	2
5	Пояснительная записка сдается на проверку.	2
6	Защита курсовой работы.	2
7	Защита курсовой работы.	2
ИТОГО		14

Решение обыкновенных дифференциальных уравнений. Задача Коши

Существует множество технических систем и технологических процессов, характеристики которых непрерывно меняются со временем t. Такие явления обычно подчиняются физическим законам, которые формулируются в виде дифференциальных уравнений.

Дифференциальными называются уравнения, содержащие одну или несколько производных. Лишь очень немногие из них удаётся решить без помощи вычислительной техники. Поэтому численные методы решения дифференциальных уравнений играют важную роль в практике инженерных расчётов.

В зависимости от числа независимых переменных и типа входящих в них производных дифференциальные уравнения делятся на две существенно различные категории: обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называются частными. В этой главе рассматриваются методы решения обыкновенных дифференциальных уравнений.

Постановка задачи

Задачу Коши можно сформулировать следующим образом.

Численное решение задачи Коши сводится к табулированию искомой функции.

График решения дифференциального уравнения называется интегральной кривой.

Геометрический смысл задачи:

- тангенс угла наклона касательной к графику решения в точке ( x, y ) к оси ОХ, - угловой коэффициент (рис.1).

а tg(α ) = f(x, y)

Существование решения:

Если правая часть f ( x, y ) непрерывна в некоторой области R, определяемой неравенствами

|x – x ₀| < a; |y – y ₀| < b

Это решение единственно, если в R выполнено условие Липшица

12 3 Следующая ⇒

Последнее изменение этой страницы: 2019-10-04; Просмотров: 195; Нарушение авторского права страницы