Ускорение материальной точки, совершающей гармонические колебания

= -A w ² cos( w t+ j _o )

{a = -A w ² sin( w t+ j _o )}.

Динамическое уравнение гармонических колебаний

 

 или

где .

Полная механическая энергия материальной точки, совершающей гармонические колебания

.

 

Период колебаний маятника:

 

– пружинного

– математического

– физического

 

где J - момент инерции маятника; a - расстояние от центра масс маятника до оси колебаний.

 

Уравнение затухающих колебаний

 или ,

 

где r - коэффициент сопротивления среды; d = 2r/m - коэффициент затухания; w - частота затухающих колебаний.

 

Решение уравнения затухающих колебаний

 

x = A_oe^{- d t} cos( w t + j _o ),

 

где A_oe^-dt - амплитуда затухающих колебаний; - частота затухающих колебаний; w_о - частота собственных колебаний.

 

Логарифмический декремент затухающих колебаний

11                                                                                                                                  12

 

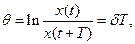
где Т - период колебаний.

 

Уравнение вынужденных колебаний

или

 

где F_ocoswt - внешняя сила, вызывающая вынужденные колебания.

Амплитуда вынужденных колебаний при резонансе

 

.

Частота вынужденных колебаний при резонансе

.

 

Релятивистская длина стержня в направлении движения со скоростью v

 или _,

 

где l_o - длина стержня в состоянии покоя (v = 0); с - скорость распространения света в вакууме; b = v/c.

 

Релятивистская масса в зависимости от скорости движения

 или

Релятивистское изменение времени

 

где Dt_o - собственное время, измеренное в состоянии покоя.

 

Релятивистский импульс частицы

Энергия покоя частицы

 

E_o = m_oc ².

 

Полная энергия релятивистской частицы

Кинетическая энергия релятивистской частицы

.

Связь между энергией и импульсом релятивистской частицы

13                                                                                                                                14

.

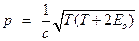Закон Гука (при продольном растяжении или сжатии)

 

s = Е e,

 

где s = F/S - нормальное напряжение, равное отношению упругой силы F к площади S поперечного сечения; Е - модуль Юнга; e = Dl/l - относительная деформация, равная отношению абсолютной деформации Dl к первоначальной длине l образца.

 

Модуль упругости при изгибе тел прямоугольного сечения

 

где Р – сила, вызывающая деформацию (изгиб); l - величина деформации (стрела прогиба); l – длина тела; а – ширина поперечного сечения тела; b – высота поперечного сечения тела.

 

Потенциальная энергия упругодеформированного образца

 

где V - объем образца.

 

Сила внутреннего трения в жидкости

,

 

где h - динамическая вязкость; v - скорость тела; dS – элемент площади жидкого слоя.

 

Сила сопротивления движению малых сферических тел в жидкости (сила Стокса)

 

F = 6 p h rv,

 

где h - динамическая вязкость; v - скорость тела; r – радиус сферы.

Примеры решения задач

 

 

Пример 1. Материальная точка начинает двигаться с ускорением а = At× i + Bt× j (А = 3 м/с³; В = 4 м/с³). Найти зависимость скорости движения материальной точки от времени, а также ее скорость и ускорение через 10 секунд после начала движения.

 

Дано:   а = At× i + Bt× j А = 3 м/с3 В = 4 м/с3 t = 10 с	В единицах СИ:	Решение. 1. В двухмерной системе координат ускорение материальной точки может быть записано в виде: Зависимость скорости движения от времени будем искать в виде: v = vx× i + vy× j. Составляющие скорости vx и vy найдем путем интегрирования из соотношений:
Найти: v(t), a(t = 10), v(t = 10)

и

 и .

Так как в начальный момент времени материальная точка покоилась, v_ox = v_oy = 0.

Тогда  и , т. е  t²× i + 2t²× j.

 

2. Модули скорости и ускорения материальной точки в любой момент времени можно представить в виде:

;

a =

Произведем вычисления значений v и a в момент времени t = 10 c.

15                                                                                                                                  16

= 250 м/с;  м/с².

Ответ. Скорость движения материальной точки изменяется со временем t по закону: t²× i + 2t²× j; в момент времени t = 10 с v = 250 м/с,             а = 50 м/с².

Пример 2. Маховик, вращаясь равнозамедленно, сделал до полной остановки 100 оборотов. Сколько времени длилось равнозамедленное движение, если начальная частота вращения была равна 20 с^-1?

 

Дано:   N =100 no=20 c-1 e = const	В единицах СИ:	Решение. Угол поворота, соответствующий  оборотам, в единицах СИ равен j = 2pN. Запишем систему уравнений движения в случае постоянного углового ускорения
Найти: t

С учетом того, что j₀ = 0, j = 2pN, w₀ = 2pn₀ и w = 0, запишем эту систему уравнений в виде:

Решаем систему уравнений. Из 2-го уравнения находим:  тогда   1-ое уравнение примет вид:  

В результате находим, что .

Подставив численные значения N и n₀, получим:

Ответ. Движение длилось 10 с.

 

Пример 3. Искусственный спутник движется вокруг Земли по круговой орбите, находящейся в плоскости экватора, на высоте h от Земли. Во время движения спутник все время находится над одной и той же точкой земной поверхности. Определить угловую скорость w, линейную скорость v и высоту полета h спутника. (Масса Земли М_з = 5, 97× 10²⁴ кг, радиус Земли R_з = 6, 37× 10⁶ м, гравитационная постоянная g = 6, 67× 10^-11 м³/(кг× с²)).

 

	Дано:   Т = 24 ч Мз = 5, 97× 1024 кг g = 6, 67× 10-11 м3/(кг× с2) Rз = 6, 37× 106 м	В единицах СИ:   Т = 8, 64× 103 с	v                F гр h                          R
Найти: w, v, h			Рис. 1.1.

 

Решение. 1. Угловую скорость спутника найдем из условия, что период его обращения вокруг Земли совпадает с периодом суточного вращения Земли Т:

                                                     (1)

2. Спутник движется по круговой орбите с ускорением  где R = R_З + h – радиус орбиты, а v - линейная скорость спутника (рис. 1.1). Это ускорение обусловлено действием силы всемирного тяготения между массой спутника m и массой Земли М_З:

                                             (2)

Подставив выражения для силы (2) и ускорения в формулу для второго закона Ньютона F = m× a, получим:

Из второго выражения находим

Легко видеть (см. рис. 1.2), что

3. Линейную скорость спутника v находим из соотношения v = w × R.

Произведем вычисления:

17                                                                                                                                  18

h = (42, 24 - 6, 37)× 10⁶ = 35, 87× 10⁶ м;

v = 7, 27× 10^-5´ 42, 24× 10⁶ = 3071 м/с.

 

Ответ. h = 35870 км; v = 3071 м/с.

 

Пример 4. На тело, движущееся со скоростью v ₀ = 3 м/с, начинает действовать сила F = 10 H. За время D t = 6 с кинетическая энергия тела увеличилась на 100 Дж. Найти скорость v₁ тела в конце действия силы и его массу т.

 

Дано: v0 = 3 м/с2 F = 10 H Dt = 2 с ∆ Ех = 100 Дж	В единицах СИ:	Решение. Изменение кинетической энергии тела можно выразить как: (3) Изменение импульса тела по второму закону Ньютона будет равно импульсу силы, то есть .
Найти: v1, т

Из этого выражения находим массу тела

                                                   (4)

После подстановки полученного выражения (4) для массы тела в выражение (3) для кинетической энергии получим:

Отсюда находим:  а

Произведем вычисления:

м/с;

Ответ. Конечная скорость тела равна 7 м/с, а масса тела – 5 кг.

 

Пример 5. Из залитого колодца, площадь дна которого S = 1 м², требуется выкачать воду на мостовую. Глубина воды в колодце     h = 2 м, а расстояние от уровня воды до мостовой Н = 5 м (рис. 1.2). Найти наименьшую работу, которую необходимо затратить на откачку воды.

 

Дано:   S = 1 м2 h = 2 м Н = 5 м r =1× 103 кг/м3	В единицах СИ:	x  H            dF h                                 dx                                                        0
Найти: А		Рис. 1.2

 

Решение. 1. Так как уровень воды будет уменьшаться при откачке, работа по ее подъему может быть найдена путем интегрирования работ по подъему отдельных слоев воды. Выберем на расстоянии x от дна колодца слой воды толщиной dx. Для подъема этого слоя на поверхность нужно преодолеть расстояние  l = H + h - x, приложив при этом силу dF, равную по величине весу слоя воды dx:

 

dF = dm × g = r × g × dV = r × g × S × dx.

 

Таким образом, работа по подъему выбранного слоя воды будет равна:

 

dA = dF × l = r × g × S × (H + h - x)dx

 

Интегрируя по всей толще воды, получим:

2. Работа по подъему воды на поверхность равна разности потенциальных энергий воды на мостовой и на дне колодца:

 

А = П₂ - П₁.

 

Потенциальная энергия воды на мостовой П₂ относительно дна колодца равна:

 

П ₂ = mg(H + h) = r × h × S × g(H + h).

	19                                                                                                                                  20

Потенциальная энергия воды в колодце, центр тяжести которой находится на высоте h/2, равна:

 

Таким образом,

Произведем вычисления:

 

Ответ. Работа по откачке воды составит 1, 17× 10⁵ Дж.

 

Пример 6. Ударная часть молота копровой установки для забивания свай, масса которой m₁ = 800 кг, падает с постоянной скоростью v ₁ = 5 м/с и забивает сваю массой m ₂ = 2 т в котлован под фундамент здания. Определить: а) величину кинетической энергии Т₁  молота при ударе; б) энергию Т₂ , затраченную на погружение сваи в грунт котлована (считая удар абсолютно неупругим); в) коэффициент полезного действия (КПД) h установки.

 

Дано:   m1 = 800 кг v1 = 5 м/с m2 = 2 т v2 = 0	В единицах СИ:   m2 = 2× 103 кг	Решение. 1. Кинетическая энергия Т1 ударной части молота, имеющая при ударе скорость v 1 = 5 м/с, равна Подставив в выражение для Т1 массу m 1 = 800 кг и скорость v1 = 5 м/с, получим:
Найти: Т1, Т2, h

 

2. Удар молота о сваю неупругий, поэтому после удара молот и свая будут двигаться вместе с одинаковой скоростью u. Величину u в момент удара найдем, воспользовавшись законом сохранения импульса при ударе

m ₁ v ₁ + m ₂ v ₂ = ( m ₁ + m ₂ ) u,

с учетом того, что v₁ и u имеют одно и то же направление, а v ₂ = 0, так как свая до удара покоилась:

                                                (5)

Скорость u молота и сваи после удара быстро уменьшается до нуля вследствие сопротивления грунта, при этом кинетическая энергия Т₂, равная

 

                                         (6)

 

расходуется на погружение сваи в грунт котлована.

Подставив (5) в (6), найдем Т₂:

 

           (7)

 

После подстановки в (7) численных значений m ₁, m ₂, Т₁ получим:

 

 

3. КПД h при ударе молота о сваю равен отношению полезной энергии Т₂, затраченной на забивание сваи в грунт котлована, к энергии Т₁ падающего молота

Подставив в это отношение выражение  получим .

После подстановки численных значений m ₁ и m ₂ получаем:

 

 

Ответ. Величина кинетической энергии ударной части молота при ударе Т₁ = 1× 10⁴ Дж; величина энергии, затраченной на погружение сваи в грунт             Т₂ @ 2, 86× 10³ Дж; КПД при ударе h @ 29%.

 

Пример 7. Маховик массой 4 кг свободно вращается с частотой 720 оборотов в минуту вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу радиусом 40 см. Через 30 с после включения постоянного тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

	21                                                                                                                                  22

Дано:   m = 4 кг n = 720 мин-1 R = 40 см Dt = 30 c w = 0	В единицах СИ:   n = 12 с-1 R = 0, 4 м	Решение. 1. Для определения тормозящего момента М сил, действующих на вращающееся тело, нужно применить основное уравнение динамики вращательного движения   M = J e,                          (8)   где J - момент инерции маховика относительно оси, проходящей через центр масс; e = D w / D t - постоянное угловое ускорение маховика. По условию задачи D w = w - w о = - w о, где wо - начальная угловая скорость маховика, т. к. конечная угловая скорость w = 0.
Найти: M, N

 

Выразим начальную угловую скорость через частоту вращения маховика  w _о = 2 p n. Тогда D w = - 2 p n, а ½ e ½ = 2 p n / D t.

Момент инерции маховика

J = mR ²,

где m - масса маховика, R - его радиус.

Тогда после подстановки выражений для J и e в (8) получим:

Произведем вычисления:

 

М = (2 × 3, 14 × 12 × 4 × 0, 16)/30 @ 1, 61   Н × м (с^-1 × кг × м²/с = Н × м).

 

2. Угол поворота, то есть угловой путь j за время вращения маховика до полной остановки, может быть определен из решения уравнения для равнозамедленного вращения

                                   (9)

После подстановки в (9) полученных выше выражений w _о = 2 p n и ½ e ½ =2 p n / D t, с учетом того, что j ₀ = 0, находим:

Так как j = 2 p N, то число оборотов маховика до его полной остановки составляет

После подстановки численных значений n и D t получаем:

 

N = 12c^-1× 30c/2 = 180.

 

Ответ. Тормозящий момент М @ 1, 61 Н× м; число оборотов, которое сделает маховик до полной остановки, N = 180.

 

Пример 8. Шарик массой т = 100 г, прикрепленный к невесомой нити длиной l ₀ = 1м, вращается в горизонтальной плоскости вокруг вертикальной оси с частотой 20 оборотов в секунду. Нить укоротили до длины l ₁ = 25 см. Определить частоту вращения шарика n ₁ и совершенную при укорачивании нити работу А.

 

Дано:   m = 100 г l 0 = 1 м l 1 = 25 см n0 = 20 с-1	В единицах СИ:   m = 0, 1 кг   l 1 = 0, 25 м	Решение: По закону сохранения момента импульса   J 0 w 0 = J 1 w 1,                  (10)   где  - момент инерции шарика при длине нити l0;  - первоначальная угловая скорость вращения;  - момент инерции шарика при длине нити l1; w 1 = 2 p n 1 - угловая скорость вращения шарика при длине нити l1.
Найти: n 1, А

Подставляя в (10) выражения для J ₀, w ₀, J ₁ и w ₁, получаем:

 откуда

Подставив численные значения n ₀, l ₀ и l ₁, получим:

 

n ₁ = 20× 1²/0, 25² = 320 c ^-1.

 

2. Работу А, совершенную при укорачивании нити, найдем как разницу между кинетическими энергиями Т₁ и Т₀, где  - кинетическая энергия вращающегося шарика после того, как укоротили нить,  - первоначальная кинетическая энергия шарика.

Произведем вычисления:

А = 2× 3, 14²× 0, 1(0, 25²× 320² - 1²× 20²) = 1, 18× 10⁴ Дж (кг × м² × с^-2 = Н × м = Дж).

Ответ. Частота вращения шарика после укорачивания нити увеличится до n ₁ = 320 c^-1; работа по укорачиванию нити А = 1, 18× 10⁴ Дж.

Пример 9. Колебательная система совершает затухающие колебания. Частота собственных колебаний системы n ₀ = 1000 Гц. Определить логарифмический декремент затухающих колебаний q, если частота затухающих колебаний n = 996 Гц.

	23                                                                                                                                  24

Дано:   n0 = 1000 Гц n = 996 Гц	В единицах СИ:	Решение. Логарифмический декремент затухания   q = d × Т,   где d – коэффициент затухания;  – период колебаний;               (11) циклическая частота затухающих колебаний; w 0 = 2 p n 0 -циклическая частота собственных колебаний.
Найти: q

Следовательно

                                         (12)

Подставляя в (12) величину  найденную из выражения (11), получаем:

Произведем вычисления

Ответ. q = 0, 563.

 

Пример 10. Вычислить, во сколько раз изменится импульс частицы, если ее кинетическая энергия Т возрастет в четыре раза? Начальная кинетическая энергия частицы Т₀ равна ее энергии покоя Т₀ = Е₀ = т₀с².

 

Дано:   Т0 = Е0 = т0с2 Т1 = 4Т0	В единицах СИ:	Решение. Связь между импульсом и энергией для релятивистской частицы определяется выражением: где Е = Е0 + Т – полная энергия частицы.
Найти: р1/р0

Следовательно:

Ответ. Импульс частицы возрастет в 2, 83 раза.

Пример 11*. Вычислить момент инерции маятника Обербека (рис. 1.3), если груз массой т = 0, 5 кг падает с высоты h = 1 м за время t = 10 с. Радиус шкива r = 20 мм, ускорение свободного падения g = 9, 81 м/с². На сколько изменится момент инерции маятника Обербека, если стержни укоротить в 3 раза, а грузы с концов стержней удалить? Масса одного груза т_гр = 100 г, масса одного стержня т_ст = 0, 2 кг, первоначальная длина стержня l = 0, 3 м.

 

Дано:   т = 0, 5 кг h = 1 м t = 10 с r = 20 мм g = 9, 81 м/с2 mгр = 100 г mст = 0, 2 кг l = 0, 3 м	В единицах СИ:     r = 2× 10-2 м   mгр = 0, 1 кг	l                                          mгр              mст           rr  r                                       m
Найти: J, ∆ J		Рис. 1.3

 

Решение. Маятник Обербека (рис. 1.3) представляет собой крестовину с четырьмя стержнями длиной l и массой т_ст. На стержни надеты одинаковые грузы массой m_гр, которые можно перемещать и фиксировать на различных расстояниях от оси вращения. Крестовина закреплена на шкиве радиуса r. На шкив наматывается нить, к свободному концу которой прикреплен груз массой m. Груз, опускаясь (падая) с высоты h, приведет маятник Обербека во вращение с угловым ускорением e. Трением обычно пренебрегают.

1. Рассмотрим падение груза т с высоты h. В качестве системы отсчета выберем двухкоординатную систему xOy, начало которой (точку О) поместим на уровне пола, при этом ось Ох направлена вверх, а ось Oz направлена параллельно оси вращения маятника.

На груз т действует сила тяжести mg и сила натяжения нити T.

Уравнение движения груза, в соответствии со вторым законом Ньютона, запишем в следующем виде:

ma = mg + T.                                               (13)

Спроецируем силы, входящие в уравнение движения (13), на ось Ох, направленную вниз в направлении движения груза из точки начала движения груза. Тогда

- ma = - mg + T.                                                  (14)

Отсюда находим:

 

25                                                                                                                                  26

T = m ( g - a ).                                              (15)

 

Падение груза m с высоты h будет равноускоренным. Модуль ускорения a при нулевой начальной скорости движения v ₀ = 0 обычно записывают в виде:

                                                  (16)

Следовательно:

                                               (17)

2. Рассмотрим вращение маятника. Согласно третьему закону Ньютона, сила Т^/,  действующая на шкив и приводящая во вращение маятник Обербека, равна по модулю силе натяжения нити Т.

⇐ Предыдущая123

Поделиться: