Кафедра «Автоматика и системотехника» Стр 1 из 5Следующая ⇒ Кафедра «Автоматика и системотехника»     Курсовой проект По предмету: Математические основы теории систем   Выполнил студент гр. УИТС-21у: Д.И. Хоменко Проверил: В.В. Воронин   Г. Хабаровск 2003 г. ЗАДАНИЕ   Курсовая работа состоит из 3-х разделов, в каждом из которых рассматривается отдельный параграф дисциплины «Математические основы теории систем». В первом разделе данной курсовой работы требуется, имея схему системы автоматического управления перейти к сигнальному графу, определить его структурные характеристики и проанализировать с помощью формулы Мезона. Во втором разделе необходимо рассмотреть логические функции, способы их задания и синтез комбинационных схем. В третьем разделе необходимо синтезировать автомат с памятью на основе содержательного описания алгоритма его работы. РЕФЕРАТ Курсовая работа содержит пояснительную записку состоящую из трех разделов на 38 листах формата А4, включающую 6 рисунков, 2 схемы, 14 таблиц и 3 литературных источника. Объектом исследования являются система автоматического управления и логическое устройство, в данном случае семисегментный элемент. Цель работы состоит в том чтобы закрепить на практике теоретический материал курса лекций «Математические основы теории систем» и приобретение навыков по анализу систем и синтезу схем. Ключевые слова: структурная схема, сигнальный граф, путь, конур, САУ, синтез схем, конечный автомат, логическая функция, таблица истинности, минимизация, карты Карно, неопределенные коэффициенты, первичные импликаты, минитермы, функциональная схема, триггер. Содержание ЗАДАНИЕ 2 РЕФЕРАТ 3 Содержание 4 Задание 1. Анализ сигнальных графов. 7 1.1  Выбор варианта задания 7 1.2 Преобразование структурной схемы к сигнальному графу 7 1.2 Преобразование структурной схемы к сигнальному графу 8 1.4 Матрица инцидентности 9 1.5 Построение бинарных матриц путей выхода для заданных контрольных точек. 10 1.6 Бинарная матрица контуров. 12 1.7 Матрица касания контуров 12 1. 8 Матрица касания путей и контуров 13 1.9 Формула Мэзона для заданного сигнального графа 13 Задание 2. Синтез комбинационных схем. 16 2.1 Определение поставленной задачи 16 2.2 Составление логических функций 19 2.2.1 Дизъюнктивная совершенная нормальная форма 19 2.2.2 Конъюнктивная совершенная нормальная форма 20 2.3 Минимизация булевых функций 20 2.3.1 Пример минимизации методом неопределенных коэффициентов 21 2.3.2 Пример минимизации методом Квайна-Мак-Класки. 22 2.3.3 Пример минимизации картами Карно 25 2.4 Совместная минимизация всех функций 26 2.5 Запись МДНФ в заданном базисе 27 3. СИНТЕЗ АВТОМАТА С ПАМЯТЬЮ 29 3.1 Анализ технического задания 29 3.2 Формальное описание абстрактного автомата 29 3.3 Кодирование входных и выходных символов состояний 31 3.4 Обобщенная функциональная схема структурного автомата 32 3.5 Каноническая система логических уравнений 33 3.6 Минимизация логических функций 35 3.7Построение комбинационной схемы автомата с памятью 35 ЗАКЛЮЧЕНИЕ 36 Приложение 1. 37 Приложение 2 38 Задание 1. Анализ сигнальных графов. 1.1 Выбор варианта задания Из букв, образующих фамилию, имя и отчество получим три множества А, В и С символов русского алфавита. Хоменко А={Х, О, М, Е, Н, К} Дмитрий B ={Д, М, И, Т, Р, Й} C ={И, Г, О, Р, Е, В, Ч} Произведя соответствующие операции над множествами получим их мощности. Из таблицы возможных мощностей методического указания выбираются типы соответствующих полученным результатам типы соединений элементов в системе автоматического управления. ½ A È B ½ = ½ { Х, О, М, Е, Н, К, Д, И, Т, Р, Й } ½ =11 ½ ( A È B ) Ç С ½ = ½ {Е, И, О, Р} ½ =4 ½ C \ A ½ = ½ {И, Г, Р, В, Ч} ½ =5 ½ A È B ½ = ½ U \ A È B ½ =33-11=22 По полученным результатам построим схему автоматического управления системой.         Рисунок 1.1.1 1.2 Преобразование структурной схемы к сигнальному графу Граф прохождения сигнала G =< x, q >, где Х – множество вершин, q - множество дуг, имеет следующие особенности. 1. Каждой вершине графа xi Î X ставится в соответствие одна переменная структурной схемы (обозначение переменных сигналов приведено на рисунке 1.1). 2. Каждой дуге ( xi, xj ) Î X поставлена в соответствие передаточная функция одного из блоков структурной схемы. 3. Если из вершины исходит несколько дуг, то для них входная величина общая. Это устраняет в графе точки разветвления. 4. Если в вершину входит несколько ребер, то соответствующая этой вершине переменная равна сумме входных сигналов. Это делает не нужным использование в графе сумматоров. Учитывая перечисленные особенности перехода от структурной схемы к сигнальному графу, перейдем от схемы рис. 1.1 к соответствующему сигнальному графу (см. рис. 1.2). Рисунок 1.2.1 Вершины отмеченные серым цветом – это заданные контрольные точки. 1.3 Матрица смежности Матицей смежности графа G называется матрица R=[rij] размером nxn, где n – число вершин графа, в которой   x x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 y x 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 x1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 x2 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 x3 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 x4 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 x5 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 x6 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 x7 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 x8 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x9 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 x10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 x11 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 x12 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 x13 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 y 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0   Матрица инцидентности Матрицей инцидентности графа G называется матрица S=[sij] размера nxm, где n – число вершин графа, а m – число дуг графа, в которой: Для построения графа пронумеруем все дуги графа в произвольном порядке, но с учетом нумерации передаточных функций.     w1 w2 w3 w4 w5 w6 w7 w8 u9 u10 u11 u12 u13 u14 u15 u16 u17 u18 u19 u20 x 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 -1 x1 1 1 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 x2 -1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 x3 0 -1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 x4 0 0 0 0 0 0 1 1 0 -1 -1 1 0 0 0 0 0 0 0 0 x5 0 0 0 0 1 0 0 0 0 0 0 -1 -1 0 0 0 0 0 0 0 x6 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 x7 0 0 0 0 0 -1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 x8 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 1 0 0 0 0 0 x9 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 1 0 0 0 0 x10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 -1 1 0 0 0 x11 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 -1 0 x12 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 x13 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 y 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 -1 1 0 0   Бинарная матрица контуров. Бинарная матрица контуров C = || cij || размера h xm, где h - число контуров, строится по следующему правилу: Предварительно пронумеруем все контуры в произвольном порядке.   w1 w2 w3 w4 w5 w6 w7 w8 u9 u10 u11 u12 u13 u14 u15 u16 u17 u18 u19 u20 1 1 0 1 1 1 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 2 1 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 0 1 3 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 0 1 4 0 1 1 1 1 1 0 0 1 0 1 0 0 1 0 0 0 1 0 1 5 0 1 1 1 0 0 1 0 1 0 1 0 0 0 1 0 1 1 0 1 6 0 1 1 1 0 0 0 1 1 0 1 0 0 0 0 1 1 1 0 1 7 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 8 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0   Матрица касания контуров Бинарная матрица контуров Ck = || cij || размера h xk, где k - число контуров, строится по следующему правилу:     1 2 3 4 5 6 7 8 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1 5 1 1 1 1 1 1 1 1 6 1 1 1 1 1 1 1 1 7 1 1 1 1 1 1 1 0 8 1 1 1 1 1 1 0 1   Для x 1   1 2 3 4 5 6 7 8 1 1 1 1 1 1 1 0 0   Для x 4   1 2 3 4 5 6 7 8 1 1 1 1 1 1 1 0 0 2 1 1 1 1 1 1 0 0   Для y   1 2 3 4 5 6 7 8 1 1 1 1 1 1 1 1 0 2 1 1 1 1 1 1 0 0 3 1 1 1 1 1 1 0 0 4 1 1 1 1 1 1 1 0 5 1 1 1 1 1 1 0 0 6 1 1 1 1 1 1 0 0   Для x13   1 2 3 4 5 6 7 8 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 0 1 3 1 1 1 1 1 1 0 1 4 1 1 1 1 1 1 1 1 5 1 1 1 1 1 1 0 1 6 1 1 1 1 1 1 0 1   Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. Таблица 2.1.1 Выходной символ	Сигнал (код)				y1	y2	y3	y4	y5	y6	y7
x4	x3	x2	x1
0	0	0	0	0	1	1	1	1	0	1	1	0
1	0	0	0	1	0	0	0	1	0	1	0	1
2	0	0	1	1	0	1	1	0	1	1	1	3
3	0	0	1	0	0	0	1	1	1	1	1	2
4	0	1	1	0	1	0	0	1	1	1	0	6
5	0	1	1	1	1	0	1	1	1	0	1	7
6	0	1	0	1	1	1	1	1	1	0	1	5
7	0	1	0	0	0	0	0	1	0	1	1	4
8	1	1	0	0	1	1	1	1	1	1	1	12
9	1	1	0	1	1	0	1	1	1	1	1	13
10	1	0	1	0	*	*	*	*	*	*	*	8
11	1	0	1	1	*	*	*	*	*	*	*	9
12	1	1	1	0	*	*	*	*	*	*	*	10
13	1	1	1	1	*	*	*	*	*	*	*	11
14	1	0	0	0	*	*	*	*	*	*	*	14
15	1	0	0	1	*	*	*	*	*	*	*	12

Если не удается заполнить все строки этой таблицы, то функция называется не полностью определенной, а наборы на которых она не определена, носят название запрещенных. В этом случае схема называется неполной. Доопределение функции производится произвольно.

Минимизация булевых функций

Минимизация сводится к поиску минимальных форм (ДНФ и КНФ). Минимальной форме соответствует самая простая логическая схема, реализующая данную функцию и требующая минимальных аппаратных затрат.

В ходе курсового проектирования была выполнена минимизация полученных булевых функций следующими методами:

1. метод неопределенных коэффициентов

2. метод Квайна-Мак-Класки

3. карты Карно

Для примера в курсовом проекте рассмотрена минимизация этими способами для функции y₃.

Пример минимизации методом неопределенных коэффициентов

Данный метод является по своим идеям наиболее простым. Для функции записываются все возможные конъюнктивные члены, которые могут входить в дизъюнктивную форму представления функции. Коэффициенты К с различными индексами являются неопределенными и подбираются так, чтобы получающаяся после этого дизъюнктивная форма была минимальной.

Если теперь задавать всевозможные наборы значений аргументов и приравнивать полученное после этого выражение значению функции на выбранных наборах, то получим систему 2⁴ уравнений для определения коэффициентов К:

Находим выражения, имеющие в правой части ноль. Исходя из определения дизъюнкции вычеркиваются все элементы в этих уравнениях и эти же элементы находящиеся в других уравнениях. В итоге получим уравнения:

Из оставшихся коэффициентов приравниваем единице коэффициент, определяющий конъюнкцию наименьшего возможного ранга, а остальные коэффициенты в левой части данного уравнения приравняем нулю(это можно сделать, так как дизъюнкция обращается а единицу, если хотя бы один член ее равен единице). Тогда уравнения примут вид:

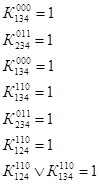
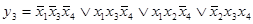
Пример минимизации методом Квайна-Мак-Класки.

При минимизации по данному методу предполагается, что минимизируемая функция задана в СДНФ. Метод Квайна – Мак – Класки состоит из последовательного выполнения следующий этапов.

Метод Квайна состоит из последовательного выполнения этапов:

1) Нахождение первичных импликант

2) Расстановка меток

3) Нахождение существенных импликант

4) Вычеркивание лишних столбцов

5) Вычеркивание лишних

6) Получение минимального покрытия

Выполним, приведенные этапы, для функции У₃.

Нахождение первичных импликант. Все минитермы (элементарные конъюнкции, входящие в ДНФ) данной функции записываются в виде их двоичных номеров. Все номера разбиваются по числу единиц в этих номерах на не пересекающиеся группы. При этом в i-тую группу войдут все номера, имеющие в своей двоичной записи ровно i единиц. По парное сравнение (склеивание) можно производить только между соседними по номеру группами. При образовании минитермов с рангом выше нулевого в разряды, соответствующие исключенным переменным, пишется знак тире. Минитермы, не склеивающиеся между собой, называются первичными импликантами.

СДНФ, которую мы нашли ранее, для функции У₃ имеет вид:

Составим минитермы для этой функции:

Таблица 2.2.1

Минитермы длиной 4

Минитермы длиной 3

Расстановка меток. Остальные этапы нужны, чтобы отбросить некоторые первичные импликанты. На данном этапе составляется таблица, число строк которой равно числу полученных первичных импликант, число столбцов совпадает с числом минитермов СДНФ. Если в некоторый минитерм СДНФ входит какая – либо из первичных импликант, то на пересечении соответствующего столбца и строки ставится метка. В таблице 2.2.2 приведем результат расстановки меток:

Таблица 2.2.2

Нахождение существенных импликант. Если в каком – либо из столбцов таблицы меток стоит только одна метка, то первичная импликанта, стоящая в соответствующей строке, называется существенной импликантой. Все существенные импликанты запоминаются. А из таблицы меток исключаются строки, соответствующие существенным импликантам, и столбцы минитермов «покрываемых» этими существенными импликантами.

Существенными являются импликанты 0-00 и -011. Поэтому вычеркиваем 1-ю и 3-ю строки и столбцы: 1, 5, 2, 7.

Составим сокращенную таблицу меток:

Таблица 2.2.3

Выбор минимального покрытия. Исследуется результирующая таблица. Выбирается такая совокупность первичных импликант, которая иссключает метки во всех столбцах (по крайней мере по одной в каждом столбце). При нескольких возможных вариантах такого выбора отдается предпочтение варианту покрытия с минимальным суммарным числом букв в простых импликантах, образующих покрытие.

 С учетом существенных импликант получим две МДНФ для этой функции имеет вид:

1.

2.

Число букв составляющих простые импликации в каждом варианте одинаково. Во втором варианте на одно отрицание меньше, поэтому берем его за искомое:

Пример минимизации картами Карно

Данный метод для минимизации функции в коде Грея. В каждую ячейку записывается значение функции на данном наборе. Затем выделяются группы ячеек размером 2^a*2^b, где a, bε [0, 1, 2…], в которых функция принимает значение «1». В каждую группу должно входить максимальное число ячеек. Таких групп должно быть минимальное количество. Каждой группе будет соответствовать конъюнктивный член размером n - a - b. Для получения МДНФ каждую группу надо просматривать в горизонтальном и вертикальном измерениях, с нахождения таких переменных, которые не меняют своего значения в пределах группы. Если переменная не меняет своего нулевого значения, то она вписывается в конъюнкцию с отрицанием, если не меняет своего единичного значения, то вписывается без отрицания. Если имеются разорванные группы, то карту Карно надо свернуть в цилиндр. На неопределенных наборах следует доопределить нулем или единицей, в соответствии с выбираемой группой ячеек. Каждая единичная ячейка должна быть включена хотя бы в одну группу.

Составим карту Карно для функции У₃ (рисунок 2.3.1).

Рис. 2.3.1 Карта Карно для функции У₃

Таким образом, для функции У₃ в МДНФ будет иметь следующий вид:

Рис. 2.6.1 графическое обозначение логических элементов

а)элемент « НЕ » б) элемент « ИЛИ » в) элемент « И » г) элемент в базисе « И-НЕ »

Построим функциональную схему на основе базиса { И-НЕ }( Приложение 1).

СИНТЕЗ АВТОМАТА С ПАМЯТЬЮ

3.1 Анализ технического задания

В данном разделе курсовой работы необходимо синтезировать автомат с памятью на основе содержательного описания алгоритма его работы.

Автомат управляет грузовым лифтом.

Грузовой лифт, обслуживает трехэтажный магазин, имеет кнопку вызова на каждом этаже и работает по следующим правилам: если нажата одна кнопка, то лифт движется на соответствующий этаж; если нажато одновременно несколько кнопок, то лифт движется на самый нижний из всех этажей на которые нажаты кнопки. Ни одна кнопка не может быть нажата во время движения.

Согласно заданию на курсовую работу, в качестве элементов памяти следует использовать D – триггеры.

Таблица 3.2.1

Таблица переходов – выходов представлена в таблице 3.2.2.                 

Таблица 3.2.2

Для того, чтобы хранить текущее состояние требуется n =[ log_θ M ] элементов памяти, где М – мощность алфавита состояний, θ – число состояний элементов памяти. Таким образом, необходимо log₂3=2 элементов памяти.

Таблица 3.3.1

Х	х3	х2	х1
х1	0	0	0
х2	0	0	1
х3	0	1	0
х4	0	1	1
х5	1	0	0
х6	1	0	1
х7	1	1	0
х8	1	1	1

 Кодирование выходных символов представлено в таблице 3.3.2.

Таблица 3. 3.2

Кодирование состояний автомата представлено в таблиц 3.3.3.

Таблица 3.3.3

В соответствии с таблицами 3.3.1 – 3.3.3 составляем таблицу переходов – входов в кодированном виде.

Таблица 3.3.4

А также составим кодированную таблицу переходов выходов.

Таблица 3.4.5

Рис.3.4.1

На рисунке 3.4.1 функциональная схема состоит из двух блоков. Первый блок - блок памяти, который состоит из двух элементов памяти (D – триггер, П₁, П₂). Второй блок – комбинационная схема (КС₁).

Таблица 3.5.1

При построении функций возбуждения памяти автомата строят функцию входов элемента памяти. Эту функцию задают в виде таблице. Функция входов структурного автомата памяти П приведена в таблице 3.5.2.

Таблица 3.5.2