Суммирующий, дифференцирующий, интегрирующий усилители

 

На основе трех базовых схем применения строятся преобразователи аналоговых сигналов, способные выполнять математические преобразования. Некоторые из них рассмотрены ниже.

1. Суммирующий усилитель.

Это усилитель, выходной сигнал которого является суммой входных. По существу, это инвертирующий усилитель с несколькими входными сигналами.

Для точки "а" можно записать, считая ОУ идеальным:

.

Поскольку , то для токов можно записать:

; ;

;  .

Подставив выражения для токов в первую формулу, получим:    

.

Отсюда:

.

Таким образом, выходной сигнал является суммой входных, причем вклад каждого из них определяется индивидуальным коэффициентом в виде отношения сопротивлений: R _ОС / R ₁, R _ОС / R ₂ и т.д. Если принять R ₁ = R ₂ = R ₃ = R, то будет вычисляться "чистая" сумма:

 .

 

2. Интегрирующий усилитель.

Его выходной сигнал пропорционален интегралу от входного сигнала. Как известно, ток через конденсатор емкостью С определяется формулой:

.

Считая ОУ идеальным можем записать для точки "а": ,U_o =0.

;   .

 

Приравняв выражения для токов получим:

 ;   .

После интегрирования получим окончательно:      

Таким образом, выходной сигнал пропорционален интегралу от входного. Напряжение U _нач (постоянная интегрирования) может быть сделано нулевым, если перед подачей U _вх конденсатор разрядить (закоротив на время С). Произведение RC = T _и обычно называют временем интегрирования. Тогда окончательно можно записать:

.

Знак "–", не учтенный ранее, указывает на то, что знак U _вых противоположен знаку U _вх.

 

3. Дифференцирующий усилитель.

Выходной сигнал пропорционален производной от входного. Эта схема отличается от предшествующей тем, что резистор и конденсатор поменялись местами. Считая ОУ идеальным, 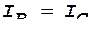 , U_o =0, можно сделать аналогичные преобразования:

;  .

Произведение Т_д= RC обычно называют временем дифференцирования.

Рассмотренные выше преобразователи широко применяются для построения судовых систем автоматики, в электронных регуляторах различных судовых систем регулирования (температуры, давления, напряжения). Регуляторы реализуют определенный закон регулирования. Наиболее совершенным является так называемый ПИД-регулятор (пропорционально-интегрально-дифференциальный), выходной сигнал которого связан с входным выражением:

.

Выходной сигнал такого регулятора является суммой трех составляющих:

- пропорциональной, суммируемой с коэффициентом k _п;

- интегральной, суммируемой с коэффициентом k _и;

- дифференциальной, суммируемой с коэффициентом k _д.

Данный регулятор может быть составлен из ранее рассмотренных преобразователей на основе ОУ. Его упрощенная схема приведена на рис. 2.18.

 

Вариант схемы ПИД-регулятора на ОУ

Рис. 2.18

 

На ОУ DA 1 выполнен пропорциональный преобразователь с коэффициентом преобразования k _п = R ₂ / R ₁, который может регулироваться переменным резистором R ₂.

На DA 2 выполнен интегральный преобразователь. Время интегрирования Т_и= R ₃ C ₁ может регулироваться с помощью R ₃, а k _и – переменным резистором R ₅.

На DA 3 выполнен дифференцирующий преобразователь. Время дифференцирования Т_д=С₂ R ₄ реализуется резистором R ₄, а k _д – резистором R ₆.

Составляющие выходного сигнала U _вых ( t ) суммируются преобразователем на DA 4.

 

Активные фильтры

 

Электрический фильтр – это устройство с заданной частотной характеристикой, т.е. пропускающее сигнал в одном диапазоне частот и не пропускающее в другом.

Активные фильтры строятся на ОУ и применяются для ослабления помех, для сглаживания пульсаций, для формирования сигналов требуемой формы Основная характеристика фильтра – амплитудно-частотная

Наиболее часто используются фильтры нижних частот (ФНЧ), пропускающие сигналы с частотой до нуля, до некоторой частоты среза (рис. 2.19). Находят применение фильтры верхних частот (ФНЧ) и фильтры полосовые, чьи характеристики даны на рис. 2.19.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться: