Алгоритм решения транспортной задачи методом потенциалов.
1. Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводят фиктивного поставщика или потребителя с недостающими запасами или запросами и нулевыми стоимостями перевозок.
2. Строят начальное опорное решение (методом северо – западного элемента, минимального элемента или методом Фогеля).
3. Опорный план проверяется на условие «вырождения». Согласно теореме Данцига количество занятых клеток в плане не должно превышать суммарного числа строк и столбцов минус единицу  (Для дальнейшего решения необходимо добиться того, чтобы количество занятых клеток в плане в точности равнялось суммарному числу строк и столбцов минус единица
(Для дальнейшего решения необходимо добиться того, чтобы количество занятых клеток в плане в точности равнялось суммарному числу строк и столбцов минус единица 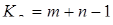 , этого можно добиться вводя при необходимости нулевые перевозки, т.е. заполняя некоторые клетки нулями), где Кз – число занятых клеток; n – число строк (пунктов отправления); m – число столбцов (пунктов назначения).
, этого можно добиться вводя при необходимости нулевые перевозки, т.е. заполняя некоторые клетки нулями), где Кз – число занятых клеток; n – число строк (пунктов отправления); m – число столбцов (пунктов назначения).
4. Строят систему потенциалов, соответствующих опорному плану. Для этого одной из строк, или одному из столбцов (обычно тому, которому соответствует большее число занятых клеток) присваивают произвольное значение «потенциал» (значение потенциала удобно брать больше, чем значение максимального тарифа) и через заполненные клетки, используя соотношение  +
+  =
= 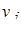 (где
(где  – потенциал строки, а
– потенциал строки, а 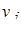 – потенциал столбца), строят систему потенциалов, т.е. получают потенциалы всех строк и столбцов. (Поясним, что предложенная для построения системы потенциалов формула
– потенциал столбца), строят систему потенциалов, т.е. получают потенциалы всех строк и столбцов. (Поясним, что предложенная для построения системы потенциалов формула  +
+  =
= 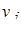 позволяет по известной себестоимости товара в пункте отправления путем прибавления к ней тарифа за транспортировку определить себестоимость товара в пункте назначения, и обратно, преобразовав формулу
позволяет по известной себестоимости товара в пункте отправления путем прибавления к ней тарифа за транспортировку определить себестоимость товара в пункте назначения, и обратно, преобразовав формулу 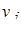 –
–  =
=  по известной себестоимости товара в пункте назначения, становится возможным, вычтя тариф за транспортировку, определить себестоимость товара в пункте отправления. Еще раз отметим, что система потенциалов строится только через заполненные клетки.)
по известной себестоимости товара в пункте назначения, становится возможным, вычтя тариф за транспортировку, определить себестоимость товара в пункте отправления. Еще раз отметим, что система потенциалов строится только через заполненные клетки.)
5. Проверяют условие оптимальности  +
+ 
 , это условие можно проверять только для свободных клеток таблицы, т.к. в заполненных оно всегда выполнено (Отметим, что невыполнение данного условия фактически означает возможность уменьшения себестоимости товара в пункте назначения, которое может быть достигнуто за счет перераспределения транспортных потоков).
, это условие можно проверять только для свободных клеток таблицы, т.к. в заполненных оно всегда выполнено (Отметим, что невыполнение данного условия фактически означает возможность уменьшения себестоимости товара в пункте назначения, которое может быть достигнуто за счет перераспределения транспортных потоков).
6. Если условие оптимальности выполнено для всех клеток матрицы, то нами получен оптимальный план перевозок (т.к. уменьшения себестоимости товара в пунктах назначения за счет перераспределения транспортных потоков невозможно) и необходимо только найти значение целевой функции L(X). Если же для какой-либо клетки условие оптимальности нарушается, то необходимо применить «формальное правило улучшения плана» и вернуться к пункту 3.
Формальное правило улучшения плана:
а) начиная с клетки, имеющей нарушение, двигаясь только по горизонталям и вертикалям, строится замкнутый контур с вершинами в занятых клетках;
б) начиная с клетки, имеющей нарушение, нумеруются вершины контура (направление обхода контура значения не имеет);
в) в четных вершинах контура находится значение минимальной перевозки;
г) для балансировки матрицы в нечетные вершины контура найденное значение прибавляется, из четных вершин – вычитается. Получается новый, улучшенный план.
Задача
Найдем оптимальное решение транспортной задачи опорный план которой представлен следующей транспортной матрицей:
| Пункты отправления, Ai
| Пункты назначения B j
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
| 110
|
| 90
|
| 10
|
|
|
|
|
|
| 5
| 8
| 1
| 2
| 0
|
| A2
|
|
|
|
| 120
|
| 50
|
|
|
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 50
|
| 15
|
|
| 9
| 2
| 3
| 2
| 0
|
Решение
Проверяем условие Данцига: 7 = 5 + 3 – 1.
Строим систему потенциалов. Задаем первой строке потенциал равный 100.
| Пункты отправления, Ai
| Пункты назначения B j
| Потенциалы
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
| 110
|
| 90
|
| 10
|
|
|
|
|
| 100
|
| 5
| 8
| 1
| 2
| 0
|
| A2
|
|
|
|
| 120
|
| 50
|
|
|
| 97
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 50
|
| 15
|
| 104
|
| 9
| 2
| 3
| 2
| 0
|
| Потенциалы
| 105
| 108
| 101
| 106
| 104
|
|
Через заполненные клетки определяем потенциалы первого, второго, и третьего столбцов. Далее через клетку (A2,B3) определяем потенциал второй строки, через клетку (A2,B4) определяем потенциал четвертого столбца. После чего через клетку (A3,B4) определяем потенциал третей строки и через клетку (A3,Bф) потенциал последнего столбца.
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,B4), где нарушение составляет 4, (A1,Bф), где нарушение составляет 4, (A2,B1), где нарушение составляет 6, (A2,B2), где нарушение составляет 6, (A2,Bф), где нарушение составляет 7 и (A3,B2), в которой нарушение составляет 2.
Применим формальное правило улучшение плана для клетки (A2,Bф), т.к. в ней выявлено наибольшее нарушение.

Получили следующий вид транспортной матрицы:
| Пункты отправления, Ai
| Пункты назначения Bj
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
| 110
|
| 90
|
| 10
|
|
|
|
|
|
| 5
| 8
| 1
| 2
| 0
|
| A2
|
|
|
|
| 120
|
| 35
|
| 15
|
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
|
| 9
| 2
| 3
| 2
| 0
|
Проверяем условие Данцига и строим систему потенциалов. Задаем первой строке потенциал, равный 100.
| Пункты отправления, Ai
| Пункты назначения Bj
| Потенциалы
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
| 110
|
| 90
|
| 10
|
|
|
|
|
| 100
|
| 5
| 8
| 1
| 2
| 0
|
| A2
|
|
|
|
| 120
|
| 35
|
| 15
|
| 97
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
| 104
|
| 9
| 2
| 3
| 2
| 0
|
| Потенциалы
| 105
| 108
| 101
| 106
| 97
|
|
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,B4), где нарушение составляет 4, (A2,B1), где нарушение составляет 6, (A2,B2), где нарушение составляет 6 и (A3,B2), в которой нарушение составляет 2.
Применим формальное правило улучшения плана для клетки (A2,B1), т.к. в ней выявлено наибольшее нарушение.

Получили следующий вид транспортной матрицы:
| Пункты отправления, Ai
| Пункты назначения Bj
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
| 90
|
| 120
|
|
|
|
|
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
|
|
| 10
|
| 35
|
| 15
|
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
|
| 9
| 2
| 3
| 2
| 0
|
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, Ai
| Пункты назначения Bj
| Потенциалы
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
| 90
|
| 120
|
|
|
|
|
| 103
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
|
|
| 10
|
| 35
|
| 15
|
| 100
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
| 107
|
| 9
| 2
| 3
| 2
| 0
|
| Потенциалы
| 102
| 111
| 104
| 109
| 100
|
|
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,B4), где нарушение составляет 4, (A2,B2), где нарушение составляет 6 и (A3,B2), в которой нарушение составляет 2.
Применим формальное правило улучшение плана для клетки (A2,B2), т.к. в ней выявлено наибольшее нарушение.

Получили следующий вид транспортной матрицы:
| Пункты отправления, Ai
| Пункты назначения Bj
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
| 80
|
| 130
|
|
|
|
|
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
| 10
|
|
|
| 35
|
| 15
|
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
|
| 9
| 2
| 3
| 2
| 0
|
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, Ai
| Пункты назначения Bj
| Потенциалы
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
| 80
|
| 130
|
|
|
|
|
| 97
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
| 10
|
|
|
| 35
|
| 15
|
| 100
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
| 107
|
| 9
| 2
| 3
| 2
| 0
|
| Потенциалы
| 102
| 105
| 98
| 109
| 100
|
|
Проверяем условие оптимальности. Оно не выполнено в клетке (A1,B4), где нарушение составляет 4.
Применим формальное правило улучшения плана для клетки (A1,B4).

Получили следующий вид транспортной матрицы:
| Пункты отправления, Ai
| Пункты назначения Bj
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
| 45
|
| 130
|
| 35
|
|
|
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
| 45
|
|
|
|
|
| 15
|
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
|
| 9
| 2
| 3
| 2
| 0
|
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, Ai
| Пункты назначения Bj
| Потенциалы
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
| 45
|
| 130
|
| 35
|
|
|
| 98
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
| 45
|
|
|
|
|
| 15
|
| 100
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
|
|
|
|
| 65
|
|
|
| 98
|
| 9
| 2
| 3
| 2
| 0
|
| Потенциалы
| 102
| 105
| 99
| 100
| 100
|
|
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,Bф), где нарушение составляет 2, (A3,B2), где нарушение составляет 5 и (A3,Bф), в которой нарушение составляет 2.
Применим формальное правило улучшение плана для клетки (A3,B2), т.к. в ней выявлено наибольшее нарушение.

Получили следующий вид транспортной матрицы:
| Пункты отправления, Ai
| Пункты назначения Bj
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
|
|
| 130
|
| 80
|
|
|
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
| 45
|
|
|
|
|
| 15
|
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
| 45
|
|
|
| 20
|
|
|
|
| 9
| 2
| 3
| 2
| 0
|
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, Ai
| Пункты назначения Bj
| Потенциалы
|
| B1
| B2
| B3
| B4
| Bф
|
| A1
|
|
|
|
| 130
|
| 80
|
|
|
| 103
|
| 5
| 8
| 1
| 2
| 0
|
| A2
| 110
|
| 45
|
|
|
|
|
| 15
|
| 100
|
| 2
| 5
| 4
| 9
| 0
|
| A3
|
|
| 45
|
|
|
| 20
|
|
|
| 103
|
| 9
| 2
| 3
| 2
| 0
|
| Потенциалы
| 102
| 105
| 104
| 105
| 100
|
|
Проверяем условие оптимальности. Оно выполнено во всех клетках, следовательно получен оптимальный план перевозок. Суммарные затраты за транспортировку составит:
 .
.
Отметим, что мы за нулевое приближение; мы выбрали опорный план, полученный методом «северо-западного угла», в силу чего нам и пришлось производить большое количество итераций. Если бы в качестве начального приближения был выбран опорный план, полученный методом «минимального элемента», то необходимое количество итераций было бы существенно меньше, а при выборе в качестве исходного опорного плана построенного «методом Фогеля», в данном примере вообще не пришлось бы производить итерации.
Отметим также, что при решении данного примера контуры которые мы строили, получались прямоугольные; это не всегда так, контуры могут быть различных форм, но строятся они всегда по одному принципу и в каждом случае могут быть получены единственным образом.

Системы массового обслуживания
ТЕОРИЯ
Основные параметры систем массового обслуживания
 – число каналов обслуживания (мастеров, врачей, барменов и т.п.). Измеряется в «штуках». Например, в парикмахерской работает 4 мастера, значит
– число каналов обслуживания (мастеров, врачей, барменов и т.п.). Измеряется в «штуках». Например, в парикмахерской работает 4 мастера, значит  .
.
 – максимальная длина очереди (максимальное количество мест для ожидания обслуживания). В СМО без очереди (
– максимальная длина очереди (максимальное количество мест для ожидания обслуживания). В СМО без очереди (  ) и с неограниченной очередью (
) и с неограниченной очередью (  ) этот параметр явно не участвует. Измеряется в «штуках». Например, в парикмахерской есть 3 кресла для ожидания, тогда
) этот параметр явно не участвует. Измеряется в «штуках». Например, в парикмахерской есть 3 кресла для ожидания, тогда  .
.
 – среднее время обслуживания одной заявки одним каналом (среднее время, которое тратит мастер, врач и т.п. на одного клиента, пациента; среднее время, которое тратится станцией техобслуживания на один автомобиль и т.д.). Измеряется в единицах времени. Пример: парикмахер обслуживает клиента в среднем за 40 минут:
– среднее время обслуживания одной заявки одним каналом (среднее время, которое тратит мастер, врач и т.п. на одного клиента, пациента; среднее время, которое тратится станцией техобслуживания на один автомобиль и т.д.). Измеряется в единицах времени. Пример: парикмахер обслуживает клиента в среднем за 40 минут:  мин. Этот параметр зависит только от свойств системы массового обслуживания и не зависит от входящего потока (например, если большинство клиентов уедет в отпуск, скорость работы парикмахера не поменяется).
мин. Этот параметр зависит только от свойств системы массового обслуживания и не зависит от входящего потока (например, если большинство клиентов уедет в отпуск, скорость работы парикмахера не поменяется).
 – интенсивность обслуживания одним каналом (среднее число заявок, которые обслуживает один канал за единицу времени; число заказов, обслуживаемых за единицу времени). Измеряется в «штуках» за единицу времени. Связан со среднем временем обслуживания соотношением:
– интенсивность обслуживания одним каналом (среднее число заявок, которые обслуживает один канал за единицу времени; число заказов, обслуживаемых за единицу времени). Измеряется в «штуках» за единицу времени. Связан со среднем временем обслуживания соотношением:
 .
.
Этот параметр, как и  , зависит только от свойств системы массового обслуживания и не зависит от входящего потока. Для нашего примера: интенсивность работы парикмахера
, зависит только от свойств системы массового обслуживания и не зависит от входящего потока. Для нашего примера: интенсивность работы парикмахера  клиента за минуту. Важно следить, за какую единицу времени происходит обслуживание. Нужно, чтобы
клиента за минуту. Важно следить, за какую единицу времени происходит обслуживание. Нужно, чтобы  и
и  были отнесены к одной единице времени (день, час, минута и т.п.). Через эту единицу будут выражаться все остальные параметры задачи, зависящие от времени или отражающие средние времена. В примере нужно перевести
были отнесены к одной единице времени (день, час, минута и т.п.). Через эту единицу будут выражаться все остальные параметры задачи, зависящие от времени или отражающие средние времена. В примере нужно перевести  из клиентов в минуту в клиентов в рабочий день. Так как в рабочем дне 8 часов по 60 минут, то
из клиентов в минуту в клиентов в рабочий день. Так как в рабочем дне 8 часов по 60 минут, то  клиентов в день.
клиентов в день.
 – интенсивность внешнего потока (среднее число заявок в единицу времени; число клиентов, пациентов и т.п., обращающихся в единице времени). Измеряется в «штуках» за единицу времени. Пример: за восьмичасовой часовой рабочий день в салон красоты обращается в среднем 50 человек:
– интенсивность внешнего потока (среднее число заявок в единицу времени; число клиентов, пациентов и т.п., обращающихся в единице времени). Измеряется в «штуках» за единицу времени. Пример: за восьмичасовой часовой рабочий день в салон красоты обращается в среднем 50 человек:  человек в раб. день. Этот параметр зависит только от свойств входящего потока и не зависит от свойств самой системы массового обслуживания (например, при болезни парикмахера поток клиентов, приходящих на обслуживание, не меняется).
человек в раб. день. Этот параметр зависит только от свойств входящего потока и не зависит от свойств самой системы массового обслуживания (например, при болезни парикмахера поток клиентов, приходящих на обслуживание, не меняется).
 – максимальное время ожидания требованием начала обслуживания (время, после которого портится не обслуженный продукт, уходит нетерпеливый клиент, станивится неактуальным выполнение заказа и т.п.). Измеряется в единицах времени. СМО в этом случае носят название систем массового обслуживания с ограниченным временем ожидания. Необходимо, чтобы время
– максимальное время ожидания требованием начала обслуживания (время, после которого портится не обслуженный продукт, уходит нетерпеливый клиент, станивится неактуальным выполнение заказа и т.п.). Измеряется в единицах времени. СМО в этом случае носят название систем массового обслуживания с ограниченным временем ожидания. Необходимо, чтобы время  было выражено в тех же единицах, к которым приведены
было выражено в тех же единицах, к которым приведены  и
и  . Этот параметр, как и параметр
. Этот параметр, как и параметр  , зависит только от свойств входящего потока и не зависит от свойств самой системы массового обслуживания (например, неиспользуемое молоко киснет в течении трех дней вне зависимости от интенсивности работы повара и количества поваров).
, зависит только от свойств входящего потока и не зависит от свойств самой системы массового обслуживания (например, неиспользуемое молоко киснет в течении трех дней вне зависимости от интенсивности работы повара и количества поваров).
Итак, параметры  ,
,  ,
, 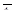 и
и  определяются свойствами обслуживающей системы, а параметры
определяются свойствами обслуживающей системы, а параметры  и
и  – свойствами входящего потока.
– свойствами входящего потока.
Параметры, которые получим в дальнейшем, определяются взаимодействием обслуживающей системы и потока.
 – интенсивность нагрузки. Безразмерная величина. До вычисления
– интенсивность нагрузки. Безразмерная величина. До вычисления  параметры
параметры  и
и  обязательно должны быть приведены к единой единице времени!
обязательно должны быть приведены к единой единице времени!
 (1)
(1)
 – вероятность того, что занято ровно
– вероятность того, что занято ровно  каналов обслуживания или доля общего времени работы СМО в течении которого заняты ровно
каналов обслуживания или доля общего времени работы СМО в течении которого заняты ровно  каналов. Безразмерная величина, находится в диапазоне от 0 до 1.
каналов. Безразмерная величина, находится в диапазоне от 0 до 1.
 – доля времени, когда все каналы свободны. Безразмерная величина, находится в диапазоне от 0 до 1. Является промежуточной величиной расчета всех СМО. Через нее выражаются многие остальные параметры. Безразмерная величина, находится в диапазоне от 0 до 1.
– доля времени, когда все каналы свободны. Безразмерная величина, находится в диапазоне от 0 до 1. Является промежуточной величиной расчета всех СМО. Через нее выражаются многие остальные параметры. Безразмерная величина, находится в диапазоне от 0 до 1.
 – вероятность того, что все каналы обслуживания заняты (заняты все мастера, врачи и т.д.). Безразмерная величина, находится в диапазоне от 0 до 1. Иначе говоря, это доля времени, в которое поступившая заявка попадает в очередь или получает отказ, если очереди нет или она максимально заполнена.
– вероятность того, что все каналы обслуживания заняты (заняты все мастера, врачи и т.д.). Безразмерная величина, находится в диапазоне от 0 до 1. Иначе говоря, это доля времени, в которое поступившая заявка попадает в очередь или получает отказ, если очереди нет или она максимально заполнена.
 – вероятность отказа в обслуживании или доля из общего числа требований, которым будет отказано в обслуживании из-за занятости всех каналов и мест ожидания или из-за превышения максимального времени ожидания. Безразмерная величина, находится в диапазоне от 0 до 1.
– вероятность отказа в обслуживании или доля из общего числа требований, которым будет отказано в обслуживании из-за занятости всех каналов и мест ожидания или из-за превышения максимального времени ожидания. Безразмерная величина, находится в диапазоне от 0 до 1.
 – вероятность обслуживания или доля из общего числа требований, которые будут обслужены. Безразмерная величина, находится в диапазоне от 0 до 1. Еще одно название – относительная эффективность обслуживания.
– вероятность обслуживания или доля из общего числа требований, которые будут обслужены. Безразмерная величина, находится в диапазоне от 0 до 1. Еще одно название – относительная эффективность обслуживания.
 (2)
(2)
 – абсолютная эффективность обслуживания (абсолютная пропускная способность). Количество требований, которые будут обслужены в единицу времени (число обслуженных за день, за час, за минуту заявок, клиентов и т.п.). Измеряется в «штуках».
– абсолютная эффективность обслуживания (абсолютная пропускная способность). Количество требований, которые будут обслужены в единицу времени (число обслуженных за день, за час, за минуту заявок, клиентов и т.п.). Измеряется в «штуках».
 (3)
(3)
 – абсолютная эффективность отказа. Количество требований, получивших отказ в обслуживании в единицу времени (число клиентов, заявок и т.п., которым будет отказано в течении дня, часа, минуты). Измеряется в «штуках».
– абсолютная эффективность отказа. Количество требований, получивших отказ в обслуживании в единицу времени (число клиентов, заявок и т.п., которым будет отказано в течении дня, часа, минуты). Измеряется в «штуках».
 (4)
(4)
 – среднее число занятых каналов обслуживания (число работающих мастеров, занятых телефонов и т.п.). Измеряется в «штуках».
– среднее число занятых каналов обслуживания (число работающих мастеров, занятых телефонов и т.п.). Измеряется в «штуках».
 (5)
(5)
 – средняя длина очереди (среднее число клиентов, заявок, ожидающих начала обслуживания в очереди). Измеряется в «штуках».
– средняя длина очереди (среднее число клиентов, заявок, ожидающих начала обслуживания в очереди). Измеряется в «штуках».
 – среднее количество требований в системе (среднее число клиентов, заявок, ожидающих начала обслуживания в очереди и обслуживаемых в СМО). Измеряется в «штуках».
– среднее количество требований в системе (среднее число клиентов, заявок, ожидающих начала обслуживания в очереди и обслуживаемых в СМО). Измеряется в «штуках».
 (6)
(6)
 – среднее время, которое проводит требование в очереди (общее время, которое, в среднем, один клиент проводит в ожидании начала обслуживания и во время обслуживания). Измеряется в единицах времени. Иногда обозначается
– среднее время, которое проводит требование в очереди (общее время, которое, в среднем, один клиент проводит в ожидании начала обслуживания и во время обслуживания). Измеряется в единицах времени. Иногда обозначается  или
или  .
.
 (7)
(7)
 – среднее время, которое проводит требование в системе (время, которое, в среднем, один клиент проводит в ожидании начала обслуживания). Измеряется в единицах времени. Иногда обозначается
– среднее время, которое проводит требование в системе (время, которое, в среднем, один клиент проводит в ожидании начала обслуживания). Измеряется в единицах времени. Иногда обозначается  или
или  .
.
 (8)
(8)
Заметим, что в результате расчета по формулам,  и
и  будут выражены в той же временной единице, к которой приведены
будут выражены в той же временной единице, к которой приведены  и
и  . Иногда это не удобно для интерпретации решения (например, среднее время ожидания равно 0,03125 раб. дня). В этом случае необходимо перевести эти параметры в другую единицу измерения времени:
. Иногда это не удобно для интерпретации решения (например, среднее время ожидания равно 0,03125 раб. дня). В этом случае необходимо перевести эти параметры в другую единицу измерения времени:
Например: 
Важно понимать, что все эти величины носят средне статистический характер, то есть реализуются «в среднем» при продолжительном времени устойчивой работы системы массового обслуживания.
Формулы определения параметров различаются для разных типов СМО (связи между параметрами, определенные по формулам (1)–(8) остаются справедливыми для всех СМО). Приведем полный набор формул для СМО четырех типов. Для удобства повторим формулы (1)–(8) в каждом случае.
СМО с ограниченной очередью (  ).
).
 , (9)
, (9)
где
 (10)
(10)
 , (11)
, (11)
 – факториал числа
– факториал числа  ; по определению
; по определению  .
.
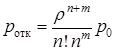 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)  (17)
(17)
где
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
СМО с неограниченной очередью (  ).
).
СМО с неограниченной очередью имеет стационарный режим работы только при условии
 .
.
При нарушении этого условия очередь неограниченно возрастает и стационарных значений параметров СМО определить не удается.
При  формулы для основных параметров данной СМО могут быть получены из формул предыдущего раздела предельным переходом
формулы для основных параметров данной СМО могут быть получены из формул предыдущего раздела предельным переходом  .
.
 , (22)
, (22)
 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
 (29)
(29)
 (30)
(30)
 (31)
(31)
 (32)
(32)
СМО без очереди (без ожидания, с отказами) (  ).
).
Формулы для основных параметров данной СМО могут быть получены из формул для СМО с ограниченной очередью, если в них положить  .
.
 , (33)
, (33)
 (34)
(34)
 (35)
(35)
 (36)
(36)
 (37)
(37)
 (38)
(38)
 (39)
(39)
 (40)
(40)
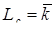 (41)
(41)
 (42)
(42)
 (43)
(43)

