Наибольшее и наименьшее значения функции на отрезке

 

       Пусть функция  непрерывна на [a, b]. Тогда по второй теореме Вейерштрасса она на этом отрезке принимает свое наименьшее значение m и наибольшее M. Если этот отрезок не содержит критических точек функции  и она дифференцируема в интервале (a, b), то ее производная знакопостоянна на этом интервале. Следовательно, функция строго монотонна на [a, b] и M равно большему, а m меньшему из значений  и . Если же функция  на [a, b] имеет конечное число критических точек, то как наибольшего M, так и наименьшего значения m она может достигать либо на концах этого отрезка, либо внутри него. В последнем случае эти значения будут одним из максимумов или минимумов функции .

       Таким образом, для нахождения наибольшего и наименьшего значения функции , непрерывной на [a, b], необходимо:

       1) найти все критические точки функции, попадающие в интервал

(a, b) и вычислить значения функции в этих точках;

       2) вычислить значение функции на концах отрезка, т.е.  и .

       3) из всех полученных значений функции выбрать наибольшее и наименьшее.

Пример

Найти наибольшее и наименьшее значение функции  на отрезке [0; 2].

Решение

1) Находим критические точки в интервале (0, 2).

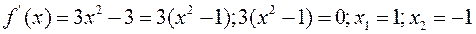 точка 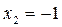 не принадлежит интервалу (0, 2), ее не рассматриваем.

2) На границах интервала

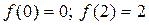
3) Выбираем наибольшее и наименьшее из полученных значений. Это

Итак,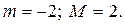

 

Направление выпуклости и точки перегиба графика функции

       Пусть функция 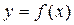 дифференцируема на интервале (a, b). Тогда существует касательная к графику функции  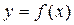в любой точке  этого графика  причем, касательная не параллельна оси Oy, поскольку ее угловой коэффициент, равный , конечен.

Определение 3.9. Будем говорить, что график функции  имеет на (a, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функций на (a, b) (рис. 3.23)

 

 

 

Рис. 3.23

 

Теорема 3.12 Если функция 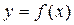 имеет на интервале (a, b) вторую производную и  ( ) во всех точках (a, b), то график функции  имеет на (a, b) выпуклость, направленную вниз (вверх).

Геометрический смысл признака:

, т.е. 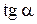 возрастает, график вогнут;

, т.е. 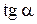 убывает, график выпуклый.

Пример

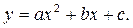
 график функции вогнут для всех x; 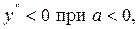 график выпуклый для всех x.

Замечание. Признак не является необходимым, т.е. в точке выпуклости или вогнутости может быть .

Пример.  (рис. 3.24)

 

                                                                         Рис. 3.24

Определение 3.10. Точка  называется точкой перегиба графика функции , если в точке M график имеет касательную, и существует такая окрестность точки 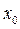, в пределах которой график функции  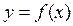слева и справа от точки  имеет разные направления выпуклости.

 

Теорема 3.13. (необходимое условие точки перегиба). Пусть график функции  имеет перегиб в точке  и пусть функция  имеет в точке  непрерывную вторую производную. Тогда 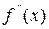 в точке  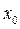обращается в нуль, т.е.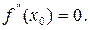

Теорема 3.14. (достаточное условие точки перегиба). Пусть функция  имеет вторую производную в некоторой окрестности точки 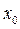. Тогда, если в пределах указанной окрестности  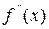имеет разные знаки слева и справа от точки 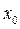, то график  имеет перегиб в точке .

Замечание. Теорема остается верной, если  имеет вторую производную в некоторой окрестности точки , за исключением самой точки 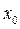, и существует касательная к графику функции в точке M. Тогда, если в пределах указанной окрестности  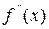имеет разные знаки слева и справа от точки 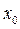, то график функции  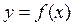имеет перегиб  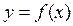имеет перегиб в точке .

Пример. ;  В точке 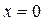 вторая производная не существует, но слева и справа от нее имеет разные знаки и график функции имеет перегиб в точке  (рис. 3.25)

 

 

 

Рис. 3.25

⇐ Предыдущая123

Поделиться: