
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса лишь для наиболее простых систем – изолированных. На практике же большей частью приходится иметь дело с системами, взаимодействующими с окружающей средой. Для характеристики процессов, протекающих в закрытых системах, были введены новые термодинамические функции состояния: изобарно-изотермический потенциал (свободная энергия Гиббса) и изохорно-изотермический потенциал (свободная энергия Гельмгольца). Поведение всякой термодинамической системы в общем случае определяется одновременным действием двух факторов – энтальпийного, отражающего стремление системы к минимуму тепловой энергии, и энтропийного, отражающего противоположную тенденцию – стремление системы к максимальной неупорядоченности. Если для изолированных систем (Δ Н = 0) направление и предел самопроизвольного протекания процесса однозначно определяется величиной изменения энтропии системы Δ S, а для систем, находящихся при температурах, близких к абсолютному нулю (S = 0 либо S = const) критерием направленности самопроизвольного процесса является изменение энтальпии Δ Н, то для закрытых систем при температурах, не равных нулю, необходимо одновременно учитывать оба фактора. Направлением и предел самопроизвольного протекания процесса в любых системах определяет более общий принцип минимума свободной энергии: Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения. Для закрытых систем, находящихся в изобарно-изотермических либо изохорно-изотермических условиях свободная энергия принимает вид изобарно-изотермического либо изохорно-изотермического потенциалов (т.н. свободная энергия Гиббса и Гельмгольца соответственно). Данные функции называют иногда просто термодинамическими потенциалами, что не вполне строго, поскольку термодинамическими потенциалами являются также внутренняя энергия (изохорно-изэнтропный) и энтальпия (изобарно-изэнтропный потенциал). Рассмотрим закрытую систему, в которой осуществляется равновесный процесс при постоянных температуре и объеме. Выразим работу данного процесса, которую обозначим Amax (поскольку работа процесса, проводимого равновесно, максимальна), из уравнений (I.53, I.54):
Преобразуем выражение (I.69), сгруппировав члены с одинаковыми индексами:
Введя обозначение: получаем:
Функция Закрытую систему, находящуюся в изобарно-изотермических условиях, характеризует изобарно-изотермический потенциал G:
 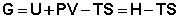 (I.74) (I.74)
Поскольку –Δ F = Amax, можно записать:
Величину А'max называют максимальной полезной работой (максимальная работа за вычетом работы расширения). Основываясь на принципе минимума свободной энергии, можно сформулировать условия самопроизвольного протекания процесса в закрытых системах. Условия самопроизвольного протекания процессов в закрытых системах: Изобарно-изотермические (P = const, T = const): Δ G < 0, dG < 0 Изохорно-изотермические (V = const, T = const): Δ F < 0, dF < 0 Процессы, которые сопровождаются увеличением термодинамических потенциалов, протекают лишь при совершении работы извне над системой. В химии наиболее часто используется изобарно-изотермический потенциал, поскольку большинство химических (и биологических) процессов происходят при постоянном давлении. Для химических процессов величину Δ G можно рассчитать, зная Δ H и Δ S процесса, по уравнению (I.75), либо пользуясь таблицами стандартных термодинамических потенциалов образования веществ Δ G°обр; в этом случае Δ G° реакции рассчитывается аналогично Δ Н° по уравнению (I.77):
Величина стандартного изменения изобарно-изотермического потенциала в ходе химической любой реакции Δ G°298 есть мера химического сродства исходных веществ. Основываясь на уравнении (I.75), можно оценить вклад энтальпийного и энтропийного факторов в величину Δ G и сделать некоторые обобщающие заключения о возможности самопроизвольного протекания химических процессов, основываясь на знаке величин Δ Н и Δ S. 1. Экзотермические реакции; Δ H < 0. а) Если Δ S > 0, то Δ G всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно. б) Если Δ S < 0, реакция будет идти самопроизвольно при Δ Н > TΔ S (низкие температуры). 2. Эндотермические реакции; Δ H > 0. а) Если Δ S > 0, процесс будет самопроизвольным при Δ Н < TΔ S (высокие температуры). б) Если Δ S < 0, то Δ G всегда положительно; самопроизвольное протекание эндотермических реакций, сопровождающихся уменьшением энтропии, невозможно. ХИМИЧЕСКОЕ РАВНОВЕСИЕ Как было показано выше, протекание самопроизвольного процесса в термодинамической системе сопровождается уменьшением свободной энергии системы (dG < 0, dF < 0). Очевидно, что рано или поздно (напомним, что понятие " время" в термодинамике отсутствует) система достигнет минимума свободной энергии. Условием минимума некоторой функции Y = f(x) является равенство нулю первой производной и положительный знак второй производной: dY = 0; d2Y > 0. Таким образом, условием термодинамического равновесия в закрытой системе является минимальное значение соответствующего термодинамического потенциала: Изобарно-изотермические (P = const, T = const): Δ G = 0 dG = 0, d2G > 0 Изохорно-изотермические (V = const, T = const): Δ F = 0 dF = 0, d2F > 0 Состояние системы с минимальной свободной энергией есть состояние термодинамического равновесия: Термодинамическим равновесием называется такое термодинамическое состояние системы, которое при постоянстве внешних условий не изменяется во времени, причем эта неизменяемость не обусловлена каким-либо внешним процессом. Учение о равновесных состояниях – один из разделов термодинамики. Далее мы будем рассматривать частный случай термодинамического равновесного состояния – химическое равновесие. Как известно, многие химические реакции являются обратимыми, т.е. могут одновременно протекать в обоих направлениях – прямом и обратном. Если проводить обратимую реакцию в закрытой системе, то через некоторое время система придет в состояние химического равновесия – концентрации всех реагирующих веществ перестанут изменяться во времени. Необходимо отметить, что достижение системой состояния равновесия не означает прекращения процесса; химическое равновесие является динамическим, т.е. соответствует одновременному протеканию процесса в противоположных направлениях с одинаковой скоростью. Химическое равновесие является подвижным – всякое бесконечно малое внешнее воздействие на равновесную систему вызывает бесконечно малое изменение состояния системы; по прекращении внешнего воздействия система возвращается в исходное состояние. Ещё одним важным свойством химического равновесия является то, что система может самопроизвольно прийти в состояние равновесия с двух противоположных сторон. Иначе говоря, любое состояние, смежное с равновесным, является менее устойчивым, и переход в него из состояния равновесия всегда связан с необходимостью затраты работы извне. Количественной характеристикой химического равновесия является константа равновесия, которая может быть выражена через равновесные концентрации С, парциальные давления P или мольные доли X реагирующих веществ. Для некоторой реакции
соответствующие константы равновесия выражаются следующим образом:
Константа равновесия есть характерная величина для каждой обратимой химической реакции; величина константы равновесия зависит только от природы реагирующих веществ и температуры. Выражение для константы равновесия для элементарной обратимой реакции может быть выведено из кинетических представлений. Рассмотрим процесс установления равновесия в системе, в которой в начальный момент времени присутствуют только исходные вещества А и В. Скорость прямой реакции V1 в этот момент максимальна, а скорость обратной V2 равна нулю:
По мере уменьшения концентрации исходных веществ растет концентрация продуктов реакции; соответственно, скорость прямой реакции уменьшается, скорость обратной реакции увеличивается. Очевидно, что через некоторое время скорости прямой и обратной реакции сравняются, после чего концентрации реагирующих веществ перестанут изменяться, т.е. установится химическое равновесие. Приняв, что V1 = V2, можно записать:
Т.о., константа равновесия есть отношение констант скорости прямой и обратной реакции. Отсюда вытекает физический смысл константы равновесия: она показывает, во сколько раз скорость прямой реакции больше скорости обратной при данной температуре и концентрациях всех реагирующих веществ, равных 1 моль/л. Теперь рассмотрим (с некоторыми упрощениями) более строгий термодинамический вывод выражения для константы равновесия. Для этого необходимо ввести понятие химический потенциал. Очевидно, что величина свободной энергии системы будет зависеть как от внешних условий (T, P или V), так и от природы и количества веществ, составляющих систему. В случае, если состав системы изменяется во времени (т.е. в системе протекает химическая реакция), необходимо учесть влияние изменения состава на величину свободной энергии системы. Введем в некоторую систему бесконечно малое количество dni молей i-го компонента; это вызовет бесконечно малое изменение термодинамического потенциала системы. Отношение бесконечно малого изменения величины свободной энергии системы к бесконечно малому количеству компонента, внесенному в систему, есть химический потенциал μ i данного компонента в системе:
Химический потенциал компонента связан с его парциальным давлением или концентрацией следующими соотношениями:
Здесь μ ° i – стандартный химический потенциал компонента (Pi = 1 атм., Сi = 1 моль/л.). Очевидно, что изменение свободной энергии системы можно связать с изменением состава системы следующим образом:
Поскольку условием равновесия является минимум свободной энергии системы (dG = 0, dF = 0), можно записать:
В закрытой системе изменение числа молей одного компонента сопровождается эквивалентным изменением числа молей остальных компонентов; т.е., для приведенной выше химической реакции имеет место соотношение:
Отсюда можно получить следующее условие химического равновесия в закрытой системе:
В общем виде условие химического равновесия можно записать следующим образом:
Выражение (I.94) носит название уравнения Гиббса – Дюгема. Подставив в него зависимость химического потенциала от концентрации, получаем:
Поскольку Σ n i μ i = Δ F, а Σ n i μ ° i = Δ F°, получаем:
Для изобарно-изотермического процесса аналогичным образом можно получить:
Полученные нами выражения I.96 – I.97 есть изотерма химическойреакции. Если система находится в состоянии химического равновесия, то изменение термодинамического потенциала равно нулю; получаем:
Здесь сi и рi – равновесные концентрации и парциальные давления исходных веществ и продуктов реакции (в отличие от неравновесных Сi и Рi в уравнениях I.96 – I.97). Поскольку для каждой химической реакции стандартное изменение термодинамического потенциала Δ F° и Δ G° есть строго определенная величина, то произведение равновесных парциальных давлений (концентраций), возведенных в степень, равную стехиометрическому коэффициенту при данном веществе в уравнении химической реакции (стехиометрические коэффициенты при исходных веществах принято считать отрицательными) есть некоторая константа, называемая константой равновесия. Уравнения (I.98, I.99) показывают связь константы равновесия со стандартным изменением свободной энергии в ходе реакции. Уравнение изотермы химической реакции связывает величины реальных концентраций (давлений) реагентов в системе, стандартного изменения термодинамического потенциала в ходе реакции и изменения термодинамического потенциала при переходе из данного состояния системы в равновесное. Знак Δ G (Δ F) определяет возможность самопроизвольного протекания процесса в системе. При этом Δ G° (Δ F°) равно изменению свободной энергии системы при переходе из стандартного состояния (Pi = 1 атм., Сi = 1 моль/л) в равновесное. Уравнение изотермы химической реакции позволяет рассчитать величину Δ G (Δ F) при переходе из любого состояния системы в равновесное, т.е. ответить на вопрос, будет ли химическая реакция протекать самопроизвольно при данных концентрациях Сi (давлениях Рi) реагентов:
Если изменение термодинамического потенциала меньше нуля, процесс в данных условиях будет протекать самопроизвольно. Популярное: |
Последнее изменение этой страницы: 2016-03-15; Просмотров: 1332; Нарушение авторского права страницы