Однофазные асинхронные двигатели

⇐ ПредыдущаяСтр 10 из 11Следующая ⇒

Однофазный двигатель имеет одну обмотку, расположенную на статоре. Однофазная обмотка, питаемая переменным током, создаст пульсирующее магнитное поле. Поместим в это поле ротор с короткозамкнутой обмоткой. Ротор вращаться не будет. Если раскрутить ротор сторонней механической силой в любую сторону, двигатель будет устойчиво работать.
Объяснить это можно следующим образом.
Пульсирующее магнитное поле можно заменить двумя магнитными полями,
вращающимися в противоположных направлениях с синхронной частотой n₁ и имеющими амплитуды магнитных потоков, равные половине амплитуды магнитного потока пульсирующего поля. Одно из магнитных полей называется прямовращающимся, другое - обратновращающимся. Каждое из магнитных полей индуктирует в роторной обмотке вихревые токи. При взаимодействии вихревых токов с магнитными полями образуются вращающие моменты, направленные встречно друг другу.
На рис. 12.7 изображены зависимости момента от прямого поля М', момента от обратного поля М" и результирующего момента М в функции скольжения М = М' - M".

Оси скольжений направлены встречно друг другу.

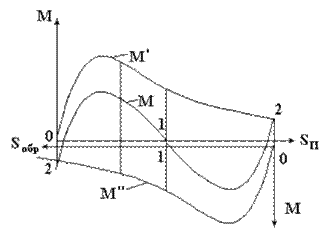
Рис. 12.7

В пусковом режиме на ротор действуют вращающие моменты, одинаковые по величине и противоположные по направлению.
Раскрутим ротор сторонней силой в направлении прямовращающегося магнитного поля. Появится избыточный (результирующий) вращающий момент, разгоняющий ротор до скорости, близкой к синхронной. При этом скольжение двигателя относительно прямовращающегося магнитного поля

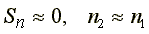Скольжение двигателя относительно обратновращающегося магнитного поля

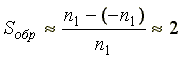Рассматривая результирующую характеристику, можно сделать следующие выводы:

1. Однофазный двигатель не имеет пускового момента. Он будет вращаться в ту сторону, в которую раскручен внешней силой.
2. Из-за тормозного действия обратновращающегося поля характеристики однофазного двигателя хуже, чем трехфазного.

Для создания пускового момента однофазные двигатели снабжают пусковой обмоткой, пространственно смещенной относительно основной, рабочей обмотки на 90^o. Пусковая обмотка подключается к сети через фазосдвигающие элементы: конденсатор или активное сопротивление.

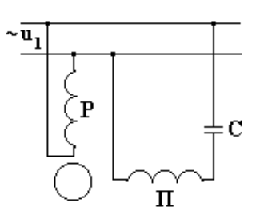На рис. 12.8 показана схема включения обмоток двигателя, где Р - рабочая обмотка, П - пусковая обмотка. Емкость фазосдвигающего элемента С подбирают таким образом, чтобы токи в рабочей и пусковой обмотках различались по фазе на 90^o.

Трехфазный асинхронный двигатель может работать от однофазной сети, если подключить его обмотки по следующим схемам.(Рис. 12.9)

В схеме на рис. 12.9а статорные обмотки соединены звездой.
В схеме на рис. 12.9б статорные обмотки соединены треугольником. Величина емкости С ≈ 60 мкф на 1 кВт мощности.

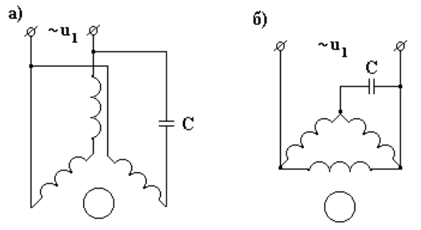
Рис. 12.9

40. Синхронные двигатели.
Конструкция, принцип действия

В отличие от асинхронного двигателя частота вращения синхронного двигателя
постоянная при различных нагрузках. Синхронные двигатели находят применение для привода машин постоянной скорости (насосы, компресоры, вентиляторы).
В статоре синхронного электродвигателя размещается обмотка, подключаемая к сети трехфазного тока и образующая вращающееся магнитное поле. Ротор двигателя состоит из сердечника с обмоткой возбуждения. Обмотка возбуждения через контактные кольца подключается к источнику постоянного тока. Ток обмотки возбуждения создает магнитное поле, намагничивающее ротор.
Роторы синхронных машин могут быть явнополюсными (с явновыраженными полюсами) и неявнополюсными (с неявновыраженными полюсами). На рис. 12.10а изображен сердечник 1 явнополюсного ротора с выступающими полюсами. На полюсах размещены катушки возбуждения 2. На рисунке 12.10б изображен неявнополюсной ротор, представляющий собой ферромагнитный цилиндр 1. На поверхности ротора в осевом направлении фрезеруют пазы, в которые укладывают обмотку возбуждения 2.

Рис. 12.10

Рассмотрим принцип работы синхронного двигателя на модели (рис. 12.11).

Вращающееся магнитное поле статора представим в виде магнита 1. Намагниченный ротор изобразим в виде магнита 2. Повернем магнит 1 на угол α. Северный магнитный полюс магнита 1 притянет южный полюс магнита 2, а южный полюс магнита 1 - северный полюс магнита 2. Магнит 2 повернется на такой же угол α. Будем вращать магнит 1. Магнит 2 будет вращаться вместе с магнитом 1, причем частоты вращения обоих магнитов будут одинаковыми, синхронными,
n₂ = n₁.

Рис. 12.11

Синхронный двигатель, на роторе которого отсутствует обмотка возбуждения, называется синхронным реактивным двигателем.
Ротор синхронного реактивного двигателя изготавливается из ферромагнитного материала и должен иметь явновыраженные полюсы. Вращающееся магнитное поле статора намагничивает ротор. Явнополюсный ротор имеет неодинаковые магнитные сопротивления по продольной и поперечной осям полюса. Силовые линии магнитного поля статора изгибаются, стремясь пройти по пути с меньшим магнитным сопротивлением. Деформация магнитного поля вызовет, вследствие упругих свойств силовых линий, реактивный момент, вращающий ротор синхронно с полем статора.
Если к вращающемуся ротору приложить тормозной момент, ось магнитного поля ротора повернется на угол θ относительно оси магнитного поля статора.
С увеличением нагрузки этот угол возрастает. Если нагрузка превысит некоторое допустимое значение, двигатель остановится, выпадет из синхронизма.
У синхронных двигателей отсутствует пусковой момент. Это объясняется тем, что электромагнитный вращающий момент, воздействующий на неподвижный ротор, меняет свое направление два раза за период Т переменного тока. Из-за своей инерционности, ротор не успевает тронуться с места и развить необходимое число оборотов.
В настоящее время применяется асинхронный пуск синхронного двигателя. В пазах полюсов ротора укладывается дополнительная короткозамкнутая обмотка.
Вращающее магнитное поле статора индуктирует в короткозамкнутой пусковой обмотке вихревые токи. При взаимодействии этих токов с магнитным полем статора образуется асинхронный электромагнитный момент, приводящий ротор во вращение. Когда частота вращения ротора приближается к частоте вращения статорного поля, двигатель втягивается в синхронизм и вращается с синхронной скоростью. Короткозамкнутая обмотка не перемещается относительно поля, вихревые токи в ней не индуктируются, асинхронный пусковой момент становится равным нулю.

41. Описать метод непосредственного применения законов Кирхгофа при анализе сложных электрических цепей с несколькими источниками энергии на следующем примере:

На рис. изображена схема разветвленной электрической цепи. Известны величины сопротивлений и ЭДС, необходимо определить токи.Укажем произвольно направления токов. Если в схеме имеется n узлов, количество независимых уравнений, которые можно составить по первому закону Кирхгофа, равно n - 1.

Для схемы на рис. 4.1 число независимых уравнений равно трем.

(4.1)

Недостающее количество уравнений составляют по второму закону Кирхгофа. Уравнения по второму закону составляют для независимых контуров. Независимым является контур, в который входит хотя бы одна новая ветвь, не вошедшая в другие контуры.
Выберем три независимых контура и укажем направления обхода контуров. Запишем три уравнения по второму закону Кирхгофа.

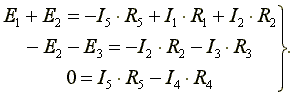(4.2)

Решив совместно системы уравнений (4.1) и (4.2), определим токи в схеме.
Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами.

42. Описать метод контурных токов при анализе сложных электрических цепей с несколькими источниками энергии на следующем примере:

Метод применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.

Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I₁₁ и I₂₂ - контурные токи.

Токи в сопротивлениях R₁ и R₂ равны соответствующим контурным токам. Ток в сопротивлении R₃, являющийся общим для обоих контуров, равен разности контурных токов I₁₁ и I₂₂, так как эти токи направлены в ветви с R₃встречно.

Порядок расчета

Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

Перегруппируем слагаемые в уравнениях

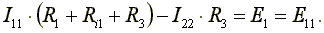(4.3)

(4.4)

Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы

, .

Сопротивление R₃, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.

где R₁₂ - общее сопротивление между первым и вторым контурами;
R₂₁ - общее сопротивление между вторым и первым контурами.
E₁₁ = E₁ и E₂₂ = E₂ - контурные ЭДС.
В общем виде уравнения (4.3) и (4.4) записываются следующим образом:

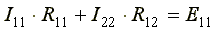Собственные сопротивления всегда имеют знак " плюс".
Общее сопротивление имеет знак " минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак " плюс", если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (4.3) и (4.4) совместно, определим контурные токи I₁₁ и I₂₂, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.

43. Описать метод узловых потенциалов при анализе сложных электрических цепей с несколькими источниками энергии на следующем примере:

Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем произвольно направления токов. Примем для схемы φ ₄ = 0.

Запишем уравнение по первому закону Кирхгофа для узла 1.

Рис. 4.3 (4.5)

В соответствии с законом Ома

где - проводимость первой ветви.

где - проводимость второй ветви.

Подставим выражения токов в уравнение (4.5).

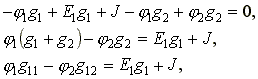(4.6)

где g₁₁ = g₁ + g₂ - собственная проводимость узла 1.

Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.
g₁₂ = g₂ - общая проводимость между узлами 1 и 2.
Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.
- сумма токов источников, находящихся в ветвях, сходящихся в узле 1.
Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком " плюс", если от узла - со знаком " минус".
По аналогии запишем для узла 2:

(4.7)

для узла 3:

(4.8)

Решив совместно уравнения (4.6), (4.7), (4.8), определим неизвестные потенциалы φ ₁, φ ₂, φ ₃, а затем по закону Ома для активной или пассивной ветви найдем токи.
Если число узлов схемы - n, количество уравнений по методу узловых потенциалов - (n - 1).

Замечание. Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше..

⇐ Предыдущая 2 3 4 5 6 7 8 91011 Следующая ⇒