
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Расчет каскадов фазовых модуляторов
Типовые схемы фазовых модуляторов и их характеристики. Фазовый модулятор - это управляемый фазовращатель. Фазовые модуляторы делятся на линейные (ЛФМ) и дискретные (ДФМ). В ЛФМ достигается линейная зависимость ϕ (t) от E(t). ДМФ можно реализовать с помощью ЛФМ, подавая на ЛФМ модулирующий сигнал в цифровой форме, однако чаще применяются специальные схемы. Требуемые модуляционные характеристики (МХ) во многом определяют структурную схему радиопередатчика. При линейных ФМ важна линейность и крутизна фазовой МХ; в идеальном случае Ф(t) = Другим параметром является диапазон модулирующих частот, в котором малы частотные искажения, т.е. закон изменения ϕ (t) не зависит от модулирующей частоты Ω. В основном частотные искажения обусловлены искажениями в подмодуляторе, динамическими искажениями в подмодуляторе, динамическими искажениями модулированного сигнала в каскадах, следующих за модулятором. К основным параметрам фазовых модуляторов относятся: · Рабочая частота; крутизна и степень линейности МХ; · Номинальный индекс модуляции; диапазон модулирующих частот (максимальная минимальная частота модуляции при модуляции гармоническим сигналом или соответствующие тактовые частоты модулирующего сигнала при дискретной ФМ); · Максимально допустимый уровень мощности высокочастного сигнала на входе модулятора и потери СВЧ мощности в модуляторе; · Степень согласования модулятора с высокочастотным трактом. Различают фазовые модуляторы отражательного и проходного типов [82, 90, 92, 93, 98], являющихся параметрическими многополюсниками. В первом (рис.6.а) по закону модуляции должна меняться фаза коэффициента отражения Г цепи, включённой в плечо 2 циркулятора. Закон изменения фазы колебания насогласованной на грузке Известны и иные устройства, осуществляющие фазовую модуляцию: схемы, основанные на преобразовании амплитудно-модулированного сигнала в фазомодулированный сигнал, схемы на двухзатворных полевых транзисторах.
Одноконтурный фазовый модулятор. Простейший вариант фазового модулятора- это колебательный контур с нелинейной емкостью, управляемой источником модулирующих колебаний. Известно, что фазовый сдвиг между напряжением При малых отклонениях ω от На практике широко используется ЛФМ, в которых в качестве управляющего элемента выступает емкость закрытого p-nперехода или барьера Шотки. Такой управляющей элемент обычно называют варикапом (на СВЧ- варактором). Простейшим ЛФМ проходного типа является одноконтурный модулятор (рис.7, а). Рис.7. Эквивалентная схема одноконтурного модулятора (а) и статическая фазовая модуляционная характеристика (б). При медленном изменении емкости контура Даже если изменения емкости пропорционально модулирующему сигналу: Интегральная оценка нелинейности фазовой МХ Даже из модели на рис.7, а ясны особенности модулятора, возникающие при использовании варикапа в качестве параметрического элемента. Выходная мощность модулятора
Рис.8. Эквивалентная схема двухконтурного линейного фазового модулятора. Нестабильность параметров предыдущего и последующего каскадов( в модели на рис.7, а –нестабильность параметров контура) также приводит к изменению МХ. Соотношения (1), (2) в сочетании с зависимостью C( Двухконтурный линейный фазовый модулятор. В одноконтурном ЛФМ линейный участок зависимости Ф(ЛС) невелик. Больше возможностей дает двухконтурный ЛФМ (рис.8, а). Пусть Комплексный коэффициент передачи тока Таблица 1
Комплекс амплитуды напряжений на контурах При резонансе ( Согласно (4) (6) В пределе при изменении Расчеты показывают, что наиболее выгодными с точки зрения обеспечения линейности МХ значениями параметров модулятора являются Из таблицы 1 видно, в каких пределах надо менять относительное модулирующее напряжение Пример. Рассчитаем ЛФМ на несущей частоте 300 МГц; номинальный индекс модуляции С помощью таблицы 1 выбираем параметры ЛФМ Оценим максимально реализуемое значение Найдем теперь проводимость нагрузки Рассчитанное таким образом значение выходной мощности соответствует границе отпирания и пробоя варикапа и поэтому является максимальным. При уменьшении выходной, а соответственно и входной мощности МХ является зависимость усредненной по первой гармонике емкости варикапа от амплитуды напряжения на нем. Чувствительность модулятора (9) составляет Контурные индуктивности Собственно высокочастотным входом ЛФМ является сечение 1-1 на рис.8, а. При резонансе входная проводимость модулятора относительно сечения 1-1 определяется выражением Для обеспечения расчетной характеристики необходимо, чтобы вещественная составляющая выходной проводимости цепи левее сечения A-Aна рис. 8, б определялась равенством На практике приходится заботиться о стабилизации МХ, в первую очередь в диапазоне рабочих температур. Одной из главных причин нестабильности МХ является нестабильность параметров источников возбуждения, в терминах рис.8, а – нестабильность проводимости Нагрузку, например 50 Ом, Следует включить в выходную цепь так, чтобы вещественная составляющая входной проводимости правее сечения D-Dна рис. 8, б составляла Для уменьшения нелинейных искажений в ФМ необходимо: · Применять варикапы с возможно большими значениями · Применять высокооборотные контуры; · Уменьшать индекс модуляции Ф; · Увеличивать коэффициент вклада варикапа в суммарную емкость контура При работе на частотах порядка десятков мегагерц типичное напряжение смещения, задающее начальную емкость, выбирают в пределах 1, 5 … 2, 5 В, а амплитуду модулирующего напряжения – около 1 В. Напряжение несущей на входе ФМ устанавливается порядка долей вольта. Фазовращатель обладает следующими свойствами: · Если контуры одинаковы и настроены в резонанс на частоту входного напряжения · Если одновременно пропорционально изменить · Входное сопротивление ФВ при изменении Существенное уменьшение Контрольные вопросы: 1. Основные характеристики угловой модуляции. 2. Спектральное представление колебаний с угловой модуляцией и их анализ. 3. Где применяются частотная модуляция? 4. Назначение АПЧ в схемах РПДУ. 5. Управители частот, их назначение.
Практическая работа №3 Расчет синтезаторов частоты Цель работы: ¾ Рассчитать синтезатор частоты ¾ Ознакомится с методическими указаниями, и выбрать схемы синтезаторов частоты Варианты структур и основные характеристики синтезатора частот Рассмотрим процесс создания синтезатора частоты (СЧ) на основе системы ФАПЧ [8, 5]. Проектирование СЧ включает в себя несколько этапов: выбор и определение структуры, расчет электрических схем отдельных узлов и экспериментальную проверку и отработку. Определение структуры синтезатора. Возможны несколько путей синтезатора [8, 12, 21, 74-77]. (Первый, наиболее широко распространенный) состоит в том, чтобы, рассмотрев известные разновидности схем и обсудив их достоинства и недостатки, выбрать наиболее подходящую к задаче синтеза и после оттого рассчитать те качественные показатели, которые характеризуют выбранную структуру. Возможное число рассматриваемых вариантов зависит от того, насколько удачно выбраны аналоги и прототипы СЧ. Второй путь отличается тем, что для определения структуры используется соотношения, связывающее различие в структуре с изменением каких-либо качественных показателей устройства. Наилучшее решение находится как оптимальная точка или область в имеющихся зависимостях. Для определения структуры по первому пути достаточно знания того математического аппарата, который предназначен для анализа схем. Для второго пути необходимо овладеть значительно более сложной методикой синтеза и знать зависимость оптимизируемых параметров СЧ от варьируемых характеристик структуры. Под оптимальной понимают структуру СЧ, которая обеспечивает экстремальное значение одного (или нескольких) параметра при заданных значениях всех других и выбранных условиях применения устройства. Если при оптимизации структур по одному из параметров решение многозначно, то всё множество полученных решений можно оптимизировать по другому параметру. Так, среди схем с оптимальной частотой характеристикой, можно выбрать схему с наибольшей полосой захвата, оптимизируя статистическую характеристику фазового детектора с этой точки зрения. Среди полученного после такой оптимизации множества можно выбрать схему с наиболее простым трактом приведения и т.д.
 Рассмотрим обобщенную структуру СЧ с кольцом ФАП (рис. 13.1.). Некоторые другие варианты структуры СЧ приведены в гл. 4. Кроме узлов, входящих в ФАПЧ, синтезатор частоты содержит: устройство предварительного приведения частоты (УППЧ), которое доводит начальную расстройку перестраиваемого генератора (ПГ) до полосы захвата ФАП; устройство формирования опорных и вспомогательных колебаний Рассмотрим обобщенную структуру СЧ с кольцом ФАП (рис. 13.1.). Некоторые другие варианты структуры СЧ приведены в гл. 4. Кроме узлов, входящих в ФАПЧ, синтезатор частоты содержит: устройство предварительного приведения частоты (УППЧ), которое доводит начальную расстройку перестраиваемого генератора (ПГ) до полосы захвата ФАП; устройство формирования опорных и вспомогательных колебаний 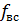 , необходимых для работы кольца автоподстройки (УФ); выходной усилитель, обеспечивающий необходимую мощность выходного колебания СЧ (ВУС) устройство управления, преобразующее внешние сигналы, определяющие частоту выходного колебания, в напряжения и перемещения, необходимые для управления частота задающими элементами синтезатора (УУ). , необходимых для работы кольца автоподстройки (УФ); выходной усилитель, обеспечивающий необходимую мощность выходного колебания СЧ (ВУС) устройство управления, преобразующее внешние сигналы, определяющие частоту выходного колебания, в напряжения и перемещения, необходимые для управления частота задающими элементами синтезатора (УУ).
Устройство приведения (ТП) основано на тракте вычитания (ТВ) и ли тракте деления (ТД) ТВ служит для преобразования множества частот входного колебания к одной частоте или к ряду частот, лежащих в диапазоне, более узком, чем диапазон частот входных колебаний тракта. ТД может быть разделён на две последовательно соединённых части: делитель с неизменным коэффициентом деления (ДПКД, Структура УФ тесно связана со структурой кольца ФАП (их особенности будут рассмотрены далее). УППЧ целесообразно рассмотреть перед проектированием кольца ФАП. Известно три способа приведения частоты. 1. Предварительная установка, осуществляемая органами установки частоты, переключаемыми или перестраивающими генераторами. 2. Предварительная подстройка, требующая введения в структуру синтезатора дополнительного кольца ЧАП, воздействующего на ПГ. 3. Поиск, осуществляемый при помощи внешнего воздействия на частотозадающие элементы ПГ, изменяющий его частоту по заранее заданному закону до тех пор, пока начальная расстройка генератора не станет меньше полосы захвата кольца ФАП. Устройства поиска подразделяются по количеству скоростей поиска на односкоростные и многоскоростные; по остаточному воздействию – на системы без запоминания и с запоминанием. Такие схемы хорошо сочетаются с кольцом ФАП, имеющим многосекционный тракт вычитания. Появление колебаний в очередной секции тракта вычитания служит сигналом для изменения скоростей поиска. Схемы поиска с запоминанием могут быть разделены по типу запоминающего устройства на механические и электрические. В механических системах а качестве ЗУ может быть применён электрический двигатель с редуктором – система, способная сохранять неизменным при отсутствие внешнего воздействия угла поворота. В этом случае датчиком сигнала управления может служить устройство, изменяющее скорость вращения двигателя по сигналам, поступающих со сравнивающего устройства, а преобразователем сигнала – потенциометр, изменяющий напряжение в зависимости от угла поворота движка. В электрической схеме в качестве ЗУ может применяться тракт счёта – делитель с переменным коэффициентом деления [75]. В этом случае датчиком сигнала управления может служить генератор импульсной последовательности, изменяющий частоту следования импульса по сигналам сравнивающего устройства, а преобразователем сигнала – преобразователь код – напряжения. Система поиска будет работать успешно при условие, что максимальный интервал между соседними частотами меньше полосы захвата и минимальный временной интервал между моментом установления на данную частоту и моментом начала перескока на следующею не меньше промежутка времени, занимаемого процессом захвата. При проектирование необходимо учитывать, что кольцо ФАП должно обладать такими параметрами и структурой, чтобы при задание любой из частот, входящих в требуемое множество, в кольце устанавливался режим синхронизации, в котором значение частоты входного колебания кольца с точностью, определяемой относительной не стабильностью частоты эталонного генератора, было бы равно заданному значению частоты выходного колебания синтезатора. Для выполнения такого равенства требуется выполнение следующих условий. 1. Диапазон собственных частот ПГ кольца ФАП должен быть таким, чтобы все множества заданных частот выходного колебания СЧ находились в нутрии этого диапазона. 2. Структура тракта приведения частот кольца ФАП и устройство формирования вспомогательных и опорных колебаний должно быть выбраны таким образом, чтобы в том случае, когда частота на входе тракта приведения ровна заданному значению частоты выходного колебания синтезатора, частота на выходе тракта приведения становилась равной частоте опорного колебания (в однозначных схемах) или кратной той частоте (в многозначных схемах). 3. Полоса захвата кольца ФАП при любом из возможных значений выбранной часты выходного колебания синтезатора должна превышать начальную расстройку, остающуюся после завершения предварительного приведения частоты. Характеристики СЧ определяющее частоту спектра выходного колебания, зависит от максимально возможно уровня внутренних и внешних помех, воздействующих на кольцо ФАП, и от фильтрующей способности кольца по отношению к этим помехам. Максимально возможный их уровень определяется уровень АЧХ функции передачи разомкнутого кольца. Характеристики управления СЧ во многом определяются параметрами кольца ФАП. Для упрощения управления структуру тракта приведения выбирают таким образом, чтобы сохранить однозначную зависимость между значением сигнала, поступающего на данную секцию тракта применения, и цифрой в соответствующем разряде числа, определяющего номинальное значение частоты выходного колебания синтезатора в десятичной системе счисления. Максимальное время установки частот СЧ связано с динамическими характеристиками кольца ФАП. Время установки частоты складывается из времени, затраченного на предварительное проведение частоты, и времени, в течение которого осуществляется захват кольца ФАП. Оговоренные условия позволяют найти основные взаимные зависимости между характеристиками СЧ и специфическими параметрами кольца ФАП, положенного в основу структуры синтезатора, и определить требования к фильтрующей способности кольца ФАП, полосе синхронизации и полосе захвата кольца. Связь между формой АЧХ и фильтрующими способностями кольца ФАП. Если характеристика управления генератора линейна и имеет крутизну
где В тех случаях, когда известна форма статической характеристики и значения рассогласований
где
В модуле функции передачи разомкнутого кольца может, выделена независимая от частоты часть, носящая название статического коэффициента усиления:
тогда В табл. 13.1 приведены зависимости
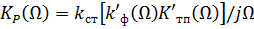 . (13.1) . (13.1)
В области частот, примыкающей к нулевой частоте,
Из табл. 13.1 и выражений (13.1), (13.2) следует, что при определенной форме статистической характеристики ФД и структуре тракта приведения задание полосы синхронизации однозначно определяет значение ВАХ функции передачи разомкнутого кольца, прилегающего к нулевой частоте. Для определения Для определения полосы захвата и характеристик переходных процессов во время захвата необходимо решать нелинейные дифференциальные уравнения. Ограничимся двумя практическими рекомендациями для увеличения полосы захвата: изменение частотной характеристики или изменение формы статической характеристики фазового детектора. Оба пути должны вести к такому изменению формы биений, которое вызовет увеличение постойной составляющей в выходном колебание фазового детектора. Для этого нужно изменять частотную характеристику таким образом, чтобы уменьшить длительность переходных процессов в схеме, а статическую характеристику – чтобы ускорить неустойчивость ветвей, уменьшив нахождение рабочей точки на этой ветви. Укороченные неустойчивые ветви имеются у статических характеристик пилообразной и трапецеидальной формы. Применение ФД с такими характеристиками ведет к увеличению полосы захвата. В кольца Популярное: |
Последнее изменение этой страницы: 2016-04-11; Просмотров: 1783; Нарушение авторского права страницы