Режим транзистора и максимальная мощность УЧ.

При расчете режима будем исходить из эквивалентной схемы УЧ, изображенной на рис. 11.2. Здесь – усредненная по первой гармонике входная проводимость транзистора, которую можно считать равной входной проводимости при коротком замыкании коллектора:

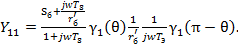
Ток управляемого генератора

Выходная проводимость транзистора на частоте n𝛚

.

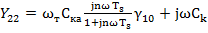В этих формулах 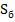и S – крутизна соответственно базового и коллекторного токов при 𝛚 → 0; , - постоянные времени в облостях активности и отсечки; - сопротивление базы; и -активная составляющая и полная емкости коллекторного перехода; = ; - максимальное значение коллекторного тока. Коэффициенты разложения (КР) в общем случае комплексные, зависят от величины и параметров инерционности и ; зависит еще от разности фаз между напряжениями и 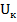. Приняв косиносуидальную аппроксимацию импульсов тока коллектора, будем считать , где θ – высокочастотный угол отсечки. В значении учтем только основную (не зависящую от ) составляющую: . В дальнейшем нас будет интересовать Re :

.

Вычислим максимально возможную мощность в нагрузке УЧ с учетом допустимых параметров транзистора: напряжения на коллекторе *, тока коллектора , напряжения на эмиттере и мощности рассеяния . При расчете будем предполагать, что транзистор находится в критическом режиме. С теми же допущениями, что и в усилителях, будем считать границей насыщения линию, проходящую через начало координат выходных характеристик с наклоном .

Если ограничено , то максимальная мощность, создаваемая генератором тока с учетом настройки выходной цепи в резонанс, 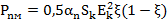, где ξ = . Отсюда . В дальнейшем величину будем использовать в качестве нормирующей.

Чтобы рассчитать мощность в нагрузке , надо учесть распределение тока генератора между и (см. рис. 11.2). В рассматриваемом режиме коэффициент распределения тока

где в активной области. Можно показать, что значения A при практически постоянны. С учетом æ мощность в нагрузке

Отсюда максимальная мощность Отметим, что эту мощность нельзя реализовать, поскольку из-за малых ξ (здесьξ =0, 05/1+A)) приходится работать с большим , а следовательно, с большим импульсом тока , который обычно больше допустимого . Величина может быть ограничена предельно допустимым током коллектора или предельно допустимым напряжением н7а эмиттерном переходе: . Исходя из последнего условия, определим допустимый 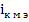ток . Ток , где – максимальное напряжение на эмиттерном переходе в активной области. Учитывая, что в области отсечки не должно превышать величину , получаем

.

Итак, если при расчете максимальной мощности исходить из допустимого тока, то .

Теперь рассчитаем мощность в критическом режиме при условии, что ограничены одновременно напряжение и ток :

.(11.7)

На первый взгляд, выражение (11.7) пр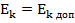и и 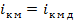должно определять максимальную мощность в нагрузке. Покажем, что это действительно так, но при одном условии. Предположим, что ограничения по отсутствуют, и введем в (11.7) безразмерный импульс тока . Тогда

.

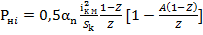Отсюда максимальная мощность получается при

,

т.е. в режиме согласования

.

Эта мощность может быть реализована, если требуемое напряжение меньше допустимого: , т.е. Z≥ . Подставив в последнее неравенство Z из(11.9.), находим критическое значение A: 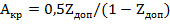. При переходе через это значение максимальная мощность (рассчитываемая при A< по (11.7.) получается в режиме согласования и определяется по (11.10). Отметим, что проведенный расчет подобен расчету мощности в нагрузке лампового генератора, выполненного по сложной схеме. Параметр æ эквивалентен в этом случае КПД промежуточного контура.

Режим согласования может быть реализован не только при работе с допустимым током, но и при . Для расчета мощности в (11.5) надо поставить и величину ξ, определенную из условия æ =0.5;

.

В результате

.

Найденные выше мощности (11.7), (11.10) и (11.12), нормированные к , предоставлены на рис 11.3, а в функции параметра A. Как видим, все три кривые пересекаются в одной точке, соответствующей равенству A= . Графики позволяют правильно ориентироваться при расчете максимальной мощности в зависимости от A, т.е. от относительного значения выходной проводимости.

Расчет УЧ на максимальную мощность в нагрузке. Заданными при расчете будем считать выходную частоту, коэффициент умножения n, параметры транзистора ( включая предельно допустимые) и высокочастотный угол отсечки.

 

Контрольные вопросы:

1. Области применения умножителей частоты в РПДУ.

2. Особенности варакторных умножителей частоты.

3. Разновидности умножителей частоты по принципу действия.

 

 

2 семестр

 

Практическая работа №1

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Популярное:

1. IV курс VIII семестр 2009/2010 уч. год
2. Non Role-Play (сокращение NonRP) - нереальная игра, действие, как данный персонаж не поступил бы в жизни. Нарушение RP режима.
3. Административная юстиция как способ обеспечения режима законности публичного управления
4. Административно – правовые режимы.
5. Анализ стационарного режима автогенератора при фиксированном смещении
6. Блокировочные схемы, обеспечивающие наладочные режимы.
7. Быстрый ввод данных в режиме Стартовый помощник
8. В зависимости от режима работы
9. Верны ли следующие суждения об авторитарном режиме?
10. Виды административно-правовых режимов
11. Визуальное определение оптимальных режимов тиснения для всех испытываемых покровных материалов.
12. Влияние режимов термообработки на качество травления проволоки