ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Э.В.БЕРЕЗИНА, Л.В.КЛИМОВИЧ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания для самостоятельной работы

Красноярск, 2008

Введение

ГЛАВА 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Законы распределения случайных величин

Законы распределения дискретных случайных величин

Биноминальное распределение.

Распределение Пуассона.

Законы распределения непрерывных случайных величин

Равномерное распределение

Показательное распределение.

Нормальный закон распределения.

Предельные теоремы теории вероятностей

Закон больших чисел

Центральная предельная теорема

Система двух случайных величин

ГЛАВА 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Самостоятельная работа по лекционному курсу

Самостоятельная работа по практическим занятиям

Вопросы для самоконтроля

Список литературы

ПРИЛОЖЕНИЯ

Введение

Развивающая форма организации учебной деятельности ориентирована на самообучение, на самостоятельную работу обучающегося. Это обусловлено требованием к быстрому обновлению научно-технических знаний. В контексте самообучения необходимо:

- самостоятельно приобретать знания, используя различные источники информации;

- обрабатывать полученную информацию;

- выбирать различные способы познавательной деятельности, соответствующие целям и задачам обучения;

- применять полученные и усвоенные знания в ходе решения различных социально-значимых и профессиональных задач и проблем;

- уметь формулировать вопросы для уточнения непонятных частей изучаемого материала.

Самостоятельная работа в структуре образовательного процесса включает в себя: внеаудиторное изучение литературы по предмету, систематическую и целенаправленную деятельность в ходе обязательных учебных занятий, творческую самостоятельную работу под руководством преподавателя.

Целью настоящих методических указаний является помощь обучаемым в организации более углубленного и расширенного изучения теоретического материала раздела «Теория вероятностей и математическая статистика».

Для успешного выполнения самостоятельной работы по теме «Теория вероятностей и математическая статистика» необходимо изучить лекции 8.1–8.8 и разобрать решение заданий учебного пособия «Теория вероятностей и математическая статистика». Для закрепления материала целесообразно решить задания для самостоятельного решения, предложенные в учебном пособии «Теория вероятностей и математическая статистика».

Методические указания написаны в соответствии с программой данной дисциплины и включают в себя две части:

- «Теория вероятностей»,

- «Математическая статистика».

ГЛАВА 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Законы распределения случайных величин

При выполнении задания этого пункта необходимо демонстрировать понимания различий между дискретной и непрерывной случайными величинами и делать выводы о законах их распределения.

Напомним основные законы распределения дискретных и непрерывных случайных величин.

Законы распределения дискретных случайных величин

Биноминальное распределение.

Дискретная случайная величина Х называется распределенной по биномиальному закону, если ее возможные значения 0, 1, ..., n, а вероятность того, что Х=k, выражается формулой

где 0< p< 1; q=1-p.

Параметры распределения n и p.

Математическое ожидание биномиального закона распределения , дисперсия , а среднее квадратичное .

Распределение Пуассона.

Дискретная случайная величина Х называется распределенной по закону Пуассона , если ее возможные значения 0, 1, 2, ... n, ..., авероятность того, что Х=k, выражается формулой:

(1.8)

где λ =np> 0 – параметр закона Пуассона.

Если известны числа l и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.

Числовые характеристики распределения Пуассона:

;

Таким образом, математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого распределения λ.

Пример 4. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех.

Решение. Вероятность появления нестандартной детали в каждом случае равна 0, 1.

Найдем вероятности того, что среди отобранных деталей:

а) вообще нет нестандартных деталей

;

б) одна нестандартная деталь

;

в) две нестандартные детали

;

г) три нестандартные детали

;

д) четыре нестандартных детали

Запишем закон распределения (табл. 1.1).

Таблица 1.1.

X
P	0, 6561	0, 2916	0, 0486	0, 0036	0, 0001

Равномерное распределение

Для того чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Непрерывная случайная величина имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю.

Рис. 1.3. Функция плотности вероятностей равномерно распределенной случайной величины

Интегральная функция распределения имеет вид:

Рис. 1.4. Интегральная функция распределения равномерно распределенной случайной величины

Определим числовые характеристики случайной величины, подчиненной равномерному закону распределения.

Вероятность попадания случайной величины в заданный интервал:

Самостоятельная работа по лекционному курсу

Выполнение данного вида работы предусматривает самостоятельное изучение (по выбору) следующих тем:

1. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ.

2. Оценка точности измерений.

3. Оценка вероятности (биномиального распределения) по относительной частоте.

4. Метод моментов для точечной оценки параметров распределения.

5. Метод наибольшего правдоподобия.

6. Другие характеристики вариационного ряда.

7. Простейшие случаи криволинейной корреляции.

8. Понятие о множественной корреляции.

9. Сравнение двух дисперсий нормальных генеральных совокупностей.

10. Проверки гипотезы о значимости выборочного коэффициента корреляции.

Все перечисленные темы можно найти литературе, представленной в конце методических указаний.

По одной из выбранных тем следует составить опорный конспект лекций, который желательно проиллюстрировать решенным самостоятельно заданием.

Самостоятельная работа по практическим занятиям

По данному виду работы предлагается построение линейной регрессионной модели по экспериментальным данным.

Создание математической модели технологического процесса или иного физического явления раскрывает перед исследователем возможность прогнозирования результатов процессов при выполнении определенных условий, изучение критических ситуаций, прогнозирование качества продукции и др.

При выполнении задания по построению регрессионной модели необходимо демонстрировать понимание терминов математической статистики, анализировать и делать выводы по полученным результатам вычислений. Выполнение данной работы направлено на систематизацию и применение знаний, полученных при изучении темы «Математическая статистика».

Рассмотрим вариант построения линейной регрессионной модели по экспериментальным данным.

Пример. В результате эксперимента получены следующие статистические данные (табл.2.1):

Таблица 2.1

x	y	x	y	x	y	x	y	x	y
8, 35	3, 50	10, 50	6, 00	11, 35	9, 50	12, 15	6, 00	12, 85	9, 50
8, 74	1, 49	10, 75	2, 50	11, 50	6, 00	12, 25	8, 05	13, 15	9, 02
9, 25	6, 40	10, 76	5, 74	11, 50	9, 00	12, 35	5, 01	13, 25	6, 49
9, 50	4, 50	11, 00	8, 50	11, 62	8, 50	12, 50	7, 03	13, 26	10, 50
9, 75	5, 00	11, 00	5, 26	11, 75	10, 00	12, 76	7, 53	13, 40	7, 51
10, 24	7, 00	11, 25	8, 00	12, 00	9, 00	12, 85	6, 01	13, 50	10, 00
13, 65	9, 50	14, 50	10, 00	13, 75	8, 51	14, 75	12, 00	14, 00	11, 00
15, 25	12, 50	14, 23	8, 40	16, 00	11, 50	14, 26	10, 00	16, 00	13, 00
14, 51	9, 50	16, 25	12, 00

Для приведенной выборки выполнить следующие задания.

1) Представить выборку в виде интервальных статистических рядов по случайным величинам X и Y.

2) Для случайной величины X построить полигон частот и гистограмму. Найти эмпирическую функцию распределения и построить ее график.

3) Найти выборочные числовые характеристики (выборочное среднее, несмещенную выборочную дисперсию, несмещенное среднее квадратичное отклонение) для случайных величин X и Y.

4) Построить доверительные интервалы для математического ожидания и дисперсии для случайной величины X с доверительной вероятностью β =0, 95.

5) Проверить гипотезу о нормальном распределении случайной величины X.

6) Провести корреляционный анализ.

7) Построить линейную регрессионную модель.

Решение. Объем выборки равен n=42.

1. Для представления выборки в виде интервальных статистических рядов определяем длины интервалов для каждой случайной величины.

Для случайной величины X наибольшим значением является 16, 25, наименьшим – 8, 35. Найдем длину интервала по X:

Выбираем h_x=1, 2. Получаем семь интервалов. От наименьшего значения 8, 35 отступим немного левее, таким образом, первый интервал начнем со значения 8, 3. Подсчитаем частоту попадания случайной величины X в каждый интервал, причем условимся, что граничное значение будет входить в больший интервал. Интервальный статистический ряд для X принимает вид (табл.2.2):

Таблица 2.2

Грани-цы интер-валов	8, 3–9, 5	9, 5–10, 7	10, 7–11, 9	11, 9–13, 1	13, 1–14, 3	14, 3–15, 5	15, 5–16, 7

Для случайной величины Y наибольшим значением является 13, 0, наименьшим – 1, 49. Найдем длину интервала по Y:

Выбираем h_y=1, 8. Получаем семь интервалов. От наименьшего значения 1, 49 отступим немного левее, таким образом, первый интервал начнем со значения 1, 5. Подсчитаем частоту попадания случайной величины Y в каждый интервал, причем условимся, что граничное значение будет входить в больший интервал. Интервальный статистический ряд для Y принимает вид (табл.2.3):

Таблица 2.3

Грани-цы интер-валов	1, 5–3, 3	3, 3–5, 1	5, 1–6, 9	6, 9–8, 7	8, 7–10, 5	10, 5–12, 3	12, 3–14, 1

2. Чтобы построить полигон частот для случайной величины X, найдем середину и относительную частоту для каждого интервала (табл.2.4).

Таблица 2.4

Границы интервалов	8, 3–9, 5	9, 5–10, 7	10, 7–11, 9	11, 9–13, 1	13, 1–14, 3	14, 3–15, 5	15, 5–16, 7
Середины интервалов	8, 9	10, 1	11, 3	12, 5	13, 7	14, 9	16, 1

На рис.2.1 по оси абсцисс отмечаем середины интервалов x_i, по оси ординат – относительные частоты .

При построении гистограммы распределения по оси абсцисс отмечаем границы интервалов, по оси ординат – относительные частоты, деленные на длину интервала (рис.2.2).

Эмпирическую функцию распределения находим по формуле:

Для того чтобы найти значение эмпирической функции распределения при данном х, достаточно подсчитать число опытов, в которых величина Х приняла значение меньше, чем х, и разделить на общее число произведенных опытов n.

Построим график эмпирической функции распределения (рис.2.3).

3. Для вычисления оценок числовых характеристик для X используем таблицу (2.5).

Таблица 2.5

Границы интервалов	Середина интервала	Частота
8, 3 – 9, 5	8, 9		26, 7	237, 63
9, 5 – 10, 7	10, 1		40, 4	408, 04
10, 7 – 11, 9	11, 3			1276, 9
11, 9 – 13, 1	12, 5			1250, 0
13, 1 – 14, 3	13, 7			1876, 9
14, 3 – 15, 5	14, 9		44, 7	666, 03
15, 5 – 16, 7	16, 1		64, 4	1036, 84
Сумма			526, 2	6752, 34

В формулу выборочного среднего подставляем сумму по четвертому столбцу (табл.2.5):

В формулу несмещенной выборочной дисперсии подставим сумму по пятому столбцу (табл.2.5):

Несмещенное выборочное среднее квадратичное отклонение:

Для вычисления оценок числовых характеристик для Y используем таблицу (2.6).

Таблица 2.6

Границы интервалов	Середина интервала	Частота
1, 5 – 3, 3	2, 4		4, 8	11, 52
3, 3 – 5, 1	4, 2		16, 8	70, 56
5, 1 – 6, 9	6, 0
6, 9 – 8, 7	7, 8		85, 8	669, 24
8, 7 – 10, 5	9, 6			921, 6
10, 5 – 12, 3	11, 4		45, 6	519, 84
12, 3 – 14, 1	13, 2		39, 6	522, 72
Сумма			336, 6	3003, 48

В формулу выборочного среднего подставляем сумму по четвертому столбцу (табл.2.6):

В формулу несмещенной выборочной дисперсии подставим сумму по пятому столбцу (табл.2.6):

Несмещенное выборочное среднее квадратичное отклонение:

4. Построим доверительные интервалы для математического ожидания и дисперсии для случайной величины X при доверительной вероятности β =0, 95.

По таблице 4 приложений находим значение статистики Стьюдента для доверительной вероятности β =0, 95 и числа степеней свободы k=42-1=41:

Половина длины доверительного интервала:

Подставляем полученные значения в формулу доверительного интервала для математического ожидания:

Для определения доверительного интервала для дисперсии по таблице 3 приложений найдем значение статистики χ ² для уровня значимости α =1–β =1–0, 95=0, 05 и числа степеней свободы k=42-1=41:

Подставим найденные значения статистики χ ² в формулу доверительного интервала для дисперсии:

Таким образом, истинные значения математического ожидания M(x)и дисперсии D(x) попадают в полученные интервалы с вероятностью β =0, 95.

5. Проверим гипотезу о нормальном распределении случайной величины X с помощью критерия Пирсона.

График полигона частот и гистограммы (внешняя схожесть с кривой Гаусса) позволяют предположить, что генеральная совокупность подчиняется нормальному закону распределения.

Выдвигаем основную гипотезу:

H₀: генеральная совокупность подчиняется нормальному закону распределения.

Тогда альтернативная гипотеза принимает вид:

H₁: закон распределения не является нормальным.

Задаемся уровнем значимости α =0, 05.

Расширяя границы первого и последнего интервалов (табл. 2.3), результаты всех вычислений сводим в таблицу 2.7.

Таблица 2.7

Границы интервалов	Частота
–∞ – 9, 5		0, 0618		0, 022
9, 5 – 10, 7	0, 11440
10, 7 – 11, 9		0, 1983	8, 3286	0, 335
11, 9 – 13, 1		0, 2396	10, 0632	0, 423
13, 1 – 14, 3		0, 2218	9, 9356	0, 082
14, 3 – 15, 5		0, 0986		0, 018
15, 5 – +∞	0, 0654
Сумма		1, 0062	1, 0000	0, 88

В таблице 2.7 четвертый столбец представляет результаты вычислений теоретических вероятностей, найденных в предположении, что случайная величина подчиняется нормальному закону распределения, по формуле:

Значения функции Лапласа можно отыскать в таблице 2 приложения.

Найдем вероятности попадания в каждый интервал:

Теоретическая частота первых двух интервалов и последних двух меньше 5, поэтому объединяем их во втором и четвертом столбцах (табл. 2.7).

Пятый столбец (табл. 2.7) является результатом вычислений по формуле:

Не следует забывать, что первых два и последние два интервала объединены.

Таким образом, суммой пятого столбца (табл.2.7) является расчетное значение критерия:

Так как после объединения осталось 5 интервалов (l=5), а по выборке определены оценки двух параметров, т.е. r=2, то число степеней свободы равно .По таблице 3 приложения найдем значение статистики для p=1–α =0, 95 и k=2:

Сравнивая полученные значения, видим, что

5, 99> 0, 88,

следовательно, гипотеза о нормальном распределении не отвергается.

6. Для проведения корреляционного анализа по данным выборки составим корреляционную таблицу (табл.2.8):

Таблица 2.8

Границы и середины интервалов для Y	Границы и середины интервалов для X
8, 3–9, 5 8, 9	9, 5–10, 7 10, 1	10, 7–11, 9 11, 3	11, 9–13, 1 12, 5	13, 1–14, 3 13, 7	14, 3–15, 5 14, 9	15, 5–16, 7 16, 1
1, 5–3, 3 2, 4		–		–	–	–	–
3, 3–5, 1 4, 2			–		–	–	–
5, 1–6, 9 6, 0						–	–
6, 9–8, 7 7, 8	–					–	–
8, 7–10, 5 9, 6	–	–					–
10, 5–12, 3 11, 4	–	–	–	–
12, 3–14, 1 13, 2	–	–	–	–	–	–

Используя полученные в пункте 3 оценки числовых характеристик, найдем выборочный корреляционный момент по формуле:

Предварительно вычислим сумму:

Выборочный коэффициент корреляции найдем по формуле:

Следует отметить, что близость выборочного коэффициента корреляции по модулю к единице является серьезным аргументом в пользу выбора линейной регрессионной модели.

7. Построим линейную регрессионную модель.

На основании метода наименьших квадратов получена линейная зависимость Y от X:

Подставляем полученные в пункте 3 оценки числовых характеристик:

Упростив выражение, окончательно получаем выборочное линейное уравнение регрессии:

Также можно построить уравнение зависимости X от Y:

Подставим полученные ранее оценки числовых характеристик:

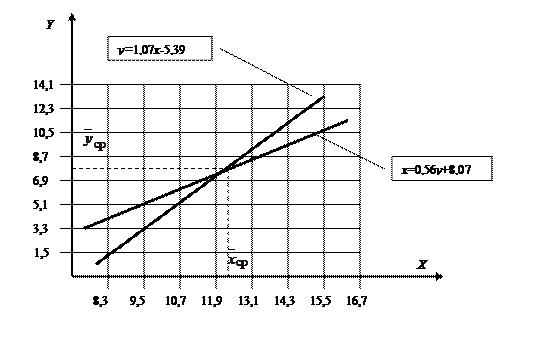
Построим обе прямые линии на корреляционном поле (рис.2.4). Прямые линии пересекаются в точке . Угол между прямыми, так называемые «ножницы», получился острым, что полностью согласуется с полученным значением выборочного коэффициента корреляции.

Полученная регрессионная модель позволяет прогнозировать значение случайной величины Y от X, и наоборот.

Рис.2.4

Вопросы для самоконтроля

1. Приведите условия осуществимости схемы Бернулли?

2. В каких случаях формулу Бернулли заменяют приближенными формулами

3. Основные виды распределений и их числовые характеристики.

4. В чем заключаются основные задачи математической статистики?

5. В чем состоит принцип выборочного метода?

6. Понятие вариационного ряда, частоты и относительной частоты.

7. Понятие статистического распределения выборки и эмпирической функции распределения.

8. Описать способы графического изображения статистического распределения.

9. Какие характеристики распределения используются в математической статистике. Привести примеры и контекст их использования.

10. Укажите свойства статистических оценок. Какими из них обладают известные характеристики распределения выборки.

11. Понятие точности и надежности интервальных оценок.

12. Понятие статистической гипотезы. Привести основные виды статистических гипотез.

13.Сформулируйте основной алгоритм проверки статистической гипотезы.

14. Какие виды критических областей Вы знаете?

15. Ошибки первого и второго рода. Способы уменьшения вероятности появления ошибки.

16. Понятие статистической и корреляционной зависимости.

17. Основные задачи теории корреляции.

18. Выборочный коэффициент регрессии и его свойства.

Список литературы

1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.: Наука, 1983.

2. Вентцель Е.С. Теория вероятностей. − М.: Высш. шк., 1998. − 578 с.

3. Вентцель, Е.С., Овчаров, Л.А. Теория вероятностей и ее инженерные приложения. -М.: Наука, 1988. - 480 с.

4. Вентцель, Е.С.Теория вероятностей: Учебник для вузов/Е.С.Венцель – 6-е изд., стереотип., - М.: Высшая шк. 1999. - 400 с.

5. Гмурман, В.Е.Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В.Е.Гмурман – 9-е изд. стереотип., - М.: Высшая шк., 2003. - 479с.

6. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие /В.Е.Гмурман – 5-е изд. стереотип., - М.: Высшая шк., 1999. - 400с.

7. Колде Я.К. Практикум по теории вероятностей и математической статистике. -М.: Высшая школа, 1991. - 157 с.

8. Колмогоров А.Н., Журбенко И.Г., Прохоров А.В. Введение в теорию вероятностей. -М.: Наука. Главная редакция физико-математической литературы, 1982. - 160 с.

9. Письменный, Д.Т.. Конспект лекций по теории вероятностей и математической статистики. – М.: Айрис-пресс, 2006. – 288с. – (Высшее образование).

10. Четыркин Е.М., Калихман И.Л. Вероятность и статистика. -М.: Финансы и статистика, 1982.- 319 с.

11. Чистяков В.П. Курс теории вероятностей. − М.: Наука, 1982.

ПРИЛОЖЕНИЯ

Таблица 1

Значения функции плотности стандартизированного нормального распределения N(0, 1)

x	0, 00	0, 01	0, 02	0, 03	0, 04	0, 05	0, 06	0, 07	0, 08	0, 09
0, 0	0, 3989	0, 3989	0, 3989	0, 3988	0, 3986	0, 3984	0, 3982	0, 3980	0, 3977	0, 3973
0, 1	0, 3970	0, 3965	0, 3961	0.3956	0, 3951	0, 3945	0, 3939	0, 3932	0, 3925	0, 3918
0, 2	0, 3910	0, 3902	0, 3894	0, 3885	0, 3876	0, 3867	0, 3857	0, 3847	0, 3836	0, 3825
0, 3	0, 3814	0, 3802	0, 3790	0, 3778	0, 3765	0, 3752	0, 3739	0, 3725	0, 3712	0, 3697
0, 4	0, 3683	0, 3668	0, 3653	0, 3637	0, 3621	0, 3605	0, 3589	0, 3572	0, 3555	0, 3538
0, 5	0, 3521	0, 3503	0, 3485	0, 3467	0, 3448	0, 3429	0, 3410	0, 3391	0, 3372	0, 3352
0, 6	0, 3332	0, 3312	0, 3292	0, 3271	0, 3251	0, 3230	0, 3209	0, 3187	0, 3166	0, 3144
0, 7	0, 3123	0, 3101	0, 3079	0, 3056	0, 3034	0, 3011	0, 2989	0, 2966	0, 2943	0, 2920
0, 8	0, 2897	0, 2874	0, 2850	0, 2827	0, 2803	0, 2780	0, 2756	0, 2732	0, 2709	0, 2685
0, 9	0, 2661	0, 2637	0, 2613	0, 2589	0, 2565	0, 2541	0, 2516	0, 2492	0, 2468	0, 2444
1, 0	0, 2420	0, 2396	0, 2371	0, 2347	0, 2323	0, 2299	0, 2275	0, 2251	0, 2227	0, 2203
1, 1	0, 2179	0, 2155	0, 2131	0, 2107	0, 2083	0, 2059	0, 2036	0, 2012	0, 1989	0, 1965
1, 2	0, 1942	0, 1919	0, 1859	0, 1872	0, 1849	0, 1826	0, 1804	0, 1781	0, 1758	0, 1736
1, 3	0, 1714	0, 1691	0, 1669	0, 1647	0, 1626	0, 1604	0, 1582	0, 1561	0, 1539	0, 1518
1, 4	0, 1497	0, 1476	0, 1456	0, 1435	0, 1415	0, 1394	0, 1374	0, 1354	0, 1334	0, 1315
1, 5	0, 1295	0, 1276	0, 1257	0, 1238	0, 1219	0, 1200	0, 1182	0, 1163	0, 1145	0, 1127
1, 6	0, 1109	0, 1092	0, 1074	0, 1057	0, 1040	0, 1023	0, 1006	0, 0989	0, 0973	0, 0957
1, 7	0, 0940	0, 0925	0, 0909	0, 0893	0, 0878	0, 0863	0, 0848	0, 0833	0, 0818	0, 0804
1, 8	0, 0790	0, 0775	0, 0761	0, 0748	0, 0734	0, 0721	0, 0707	0, 0694	0, 0681	0, 0669
1, 9	0, 0656	0, 0644	0, 0632	0, 0620	0, 0608	0, 0596	0, 0584	0, 0573	0, 0562	0, 0551
2, 0	0, 0540	0, 0529	0, 0519	0, 0508	0, 0498	0, 0488	0, 0478	0, 0468	0, 0459	0, 0449
2, 1	0, 0440	0, 0431	0, 0422	0, 0413	0, 0404	0, 0396	0, 0387	0, 0379	0, 0371	0, 0363
2, 2	0, 0355	0, 0347	0, 0339	0, 0332	0, 0325	0, 0317	0, 0310	0, 0303	0, 0297	0, 0290
2, 3	0, 0283	0, 0277	0, 0270	0, 0264	0, 0258	0, 0252	0, 0246	0, 0241	0, 0235	0, 0229
2, 4	0, 0224	0, 0219	0, 0213	0, 0208	0, 0203	0, 0198	0, 0194	0, 0189	0, 0184	0, 0180
2, 5	0, 0175	0, 0171	0, 0167	0, 0163	0, 0158	0, 0154	0, 0151	0, 0147	0, 0143	0, 0139
2, 6	0, 0136	0, 0132	0, 0129	0, 0126	0, 0122	0, 0119	0, 0116	0, 0113	0, 0110	0, 0107
2, 7	0, 0104	0, 0101	0, 0099	0, 0096	0, 0093	0, 0091	0, 0088	0, 0086	0, 0084	0, 0081
2, 8	0, 0079	0, 0077	0, 0075	0, 0073	0, 0071	0, 0069	0, 0067	0, 0065	0, 0063	0, 0061
2, 9	0, 0060	0, 0058	0, 0056	0, 0055	0, 0053	0, 0051	0, 0050	0, 0048	0, 0047	0, 0046
3, 0	0, 0044	0, 0043	0, 0042	0, 0040	0, 0039	0, 0038	0, 0037	0, 0036	0, 0035	0, 0034
3, 1	0, 0033	0, 0032	0, 0031	0, 0030	0, 0029	0, 0028	0, 0027	0, 0026	0, 0025	0, 0025
3, 2	0, 0024	0, 0023	0, 0022	0, 0022	0, 0021	0, 0020	0, 0020	0, 0019	0, 0018	0, 0018
3, 3	0, 0017	0, 0017	0, 0016	0, 0016	0, 0015	0, 0015	0, 0014	0, 0014	0, 0013	0, 0013
3, 4	0, 0012	0, 0012	0, 0012	0, 0011	0, 0011	0, 0010	0, 0010	0, 0010	0, 0009	0, 0009
3.5	0, 0009	0, 0008	0, 0008	0, 0008	0, 0008	0, 0007	0, 0007	0, 0007	0, 0007	0, 0006
3.6	0, 0006	0, 0006	0, 0006	0, 0005	0, 0005	0, 0005	0, 0005	0, 0005	0, 0005	0, 0004
3, 7	0, 0004	0, 0004	0, 0004	0, 0004	0, 0004	0, 0004	0, 0003	0, 0003	0, 0003	0, 0003
3, 8	0.0003	0, 0003	0, 0003	0, 0003	0, 0003	0, 0002	0, 0002	0, 0002	0, 0002	0, 0002
3, 9	0, 0002	0, 0002	0, 0002	0, 0002	0, 0002	0, 0002	0, 0002	0, 0002	0, 0001	0, 0001
4.0	0, 0001	0, 0001	0, 0001	0, 0001	0, 0001	0, 0001	0, 0001	0, 0001	0, 0001	0, 0001
x	0, 00	0, 01	0, 02	0, 03	0, 04	0, 05	0, 06	0, 07	0, 08	0, 09

Таблица 2

Значение функции

12	Поделиться: