Сообщение разбивается на блоки, каждый блок сообщения делится на две части, левую и правую, и проходят n раундов преобразования.
В каждом раунде новая правая часть получается как сумма по модулю два предыдущей левой части с результатом шифрования предыдущей правой части, а новая левая часть равна правой части предыдущего раунда.
Расшифровывание происходит в обратном порядке следования подключей.
Потоковые шифры
Чаще всего в качестве криптографического примитива потоковых шифров применяется регистр сдвига с линейной обратной связью (РСЛОС).
Схема РСЛОС представлена на изображении:
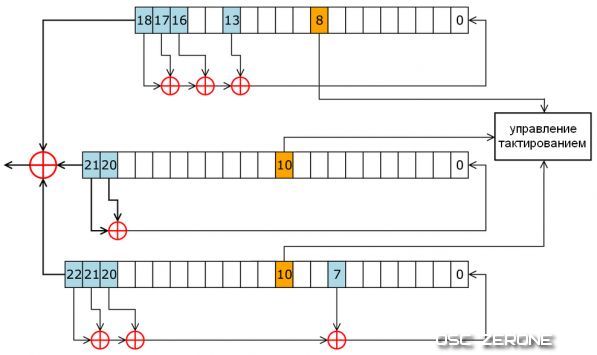
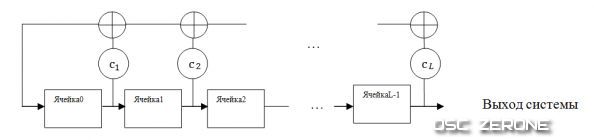Схема регистров потокового шифра А5, основанного на РСЛОС:
3. Для шифра Эль-Гамаля с заданными параметрами p, g, CB, K найти недостающие параметры и описать процесс передачи сообщения пользователю В. Дано p=23, g=7, CB= 3, K=15, m=5Для всей группы абонентов выбираются некоторое большое простое число р и число g, такие, что различные степени g суть различные числа по модулю р. Числа р и g передаются абонентам в открытом виде. Затем каждый абонент группы выбирает свое секретное число ci, 1< Ci< р-1, и вычисляет соответствующее ему открытое число di по формуле di=gcimodp.
Пусть пользователь A выбрал для себя секретное число сA = 5 и вычислил соответствующее ему открытое число da = 75 mod 23 = 17. Также поступил и пользователь B, выбрав CB= 3 и вычислив db = 73 mod 23 = 21.
Передадим сообщение m = 5 от А к В. Возьмем р = 23, g = 7.
Пользователь А выбирает случайно число k, например k = 15, и вычисляет:
r = gk mod p = 715 mod 23 = 14
е = m  dBk mod p = 5 2115 mod 23 = 12
Теперь A посылает к В зашифрованное сообщение в виде пары чисел (r, е).
В, получив (r, е), вычисляет m' = е rp-1-cBmod р = 12 1423-1-3 mod 23= 5. Мы видим, что В смог расшифровать переданное сообщение.
БИЛЕТ №39
1. Электронно-цифровая подпись.
ЭЦП - аналог ручной подписи, обеспечивающий возможность проверки, подлинности к корректности документа.Электронная цифровая подпись позволяет заменить при безбумажном документообороте традиционные печать и подпись. Цифровая подпись не имеет ничего общего с последовательностью символов, соответствующих печати или подписи, приписанной к документу. При построении цифровой подписи вместо обычной связи между печатью или рукописной подписью и листом бумаги выступает сложная математическая зависимость между документом, секретным и общедоступным ключами, а также цифровой подписью. Получение фальшивой подписи, не имея секретного ключа — задача практически нерешаемая даже для очень слабых шифров и хэшей.Электронная цифровая подпись может иметь следующее назначение: 1)Удостоверение источника документа. В зависимости от деталей определения документа могут быть подписаны такие поля, как «автор», «внесённые изменения», «метка времени» и т. д. 2)Защиту от изменений документа. При любом случайном или преднамеренном изменении документа (или подписи) изменится хэш, следовательно, подпись станет недействительной. 3)Невозможность отказа от авторства. Так как создать корректную подпись можно, лишь зная закрытый ключ, а он известен только владельцу, то владелец не может отказаться от своей подписи под документом. 4)Предприятиям и коммерческим организациям сдачу финансовой отчетности в государственные учреждения в электронном виде
2.Идентификация и проверка подлинности. Применение пароля. Основные понятия.
Идентификация– присвоение субъектам и объектам доступа личного идентификатора и сравнение его с заданным. Аутентифика́ ция - процедура проверки подлинности.
Идентификация позволяет субъекту (пользователю, процессу, действующему от имени определенного пользователя, или иному аппаратно-программному компоненту) назвать себя (сообщить свое имя). Посредством аутентификации вторая сторона убеждается, что субъект действительно тот, за кого он себя выдает. Аутентификация бывает односторонней (обычно клиент доказывает свою подлинность серверу) и двусторонней (взаимной). Пример односторонней аутентификации - процедура входа пользователя в систему.
Наиболее распространенными простыми и привычными являются методы аутентификации, основанные на паролях – конфиденциальных идентификаторах субъектов. В этом случае при вводе субъектом своего пароля подсистема аутентификации сравнивает его с паролем, хранящимся в базе эталонных данных в зашифрованном виде. В случае совпадения паролей подсистема аутентификации разрешает доступ к ресурсам системы. Парольные методы следует классифицировать по степени изменяемости паролей: 1)методы, использующие постоянные (многократно используемые) пароли, 2)методы, использующие одноразовые (динамично изменяющиеся) пароли. В большинстве случаев используются многоразовые пароли. В этом случае пароль пользователя не изменяется от сеанса к сеансу в течение установленного администратором системы времени его действительности. Это упрощает процедуры администрирования, но повышает угрозу рассекречивания пароля. Более надежный способ – использование одноразовых или динамически меняющихся паролей. Отметим, что методы аутентификации, основанные на одноразовых паролях, также не обеспечивают абсолютной защиты. Например, если злоумышленник имеет возможность подключения к сети и перехватывать передаваемые пакеты, то он может посылать последние как собственные. В последнее время получили распространение комбинированные методы идентификации и аутентификации, требующие, помимо знания пароля, наличие карточки (token) – специального устройства, подтверждающего подлинность субъекта.
3. Для шифра Эль-Гамаля с заданными параметрами p, g, CB, K найти недостающие параметры и описать процесс передачи сообщения пользователю В. Дано p=23, g=7,
CB= 3, K=15, m=5
Для всей группы абонентов выбираются некоторое большое простое число р и число g, такие, что различные степени g суть различные числа по модулю р. Числа р и g передаются абонентам в открытом виде. Затем каждый абонент группы выбирает свое секретное число ci, 1< Ci< р-1, и вычисляет соответствующее ему открытое число di по формуле di=gcimodp.
Пусть пользователь A выбрал для себя секретное число сA = 5 и вычислил соответствующее ему открытое число da = 75 mod 23 = 17. Также поступил и пользователь B, выбрав CB= 3 и вычислив db = 73 mod 23 = 21.
Передадим сообщение m = 5 от А к В. Возьмем р = 23, g = 7.
Пользователь А выбирает случайно число k, например k = 15, и вычисляет:
r = gk mod p = 715 mod 23 = 14
е = m dBk mod p = 5 2115 mod 23 = 12
Теперь A посылает к В зашифрованное сообщение в виде пары чисел (r, е).
В, получив (r, е), вычисляет m' = е rp-1-cBmod р = 12 1423-1-3 mod 23= 5. Мы видим, что В смог расшифровать переданное сообщение.
|
