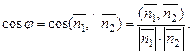В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме

 

Векторы называются линейно независимыми, если равенство

справедливо тогда и только тогда, когда 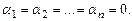В противном случае эти векторы называются линейно зависимыми. Для того чтобы векторы были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.

Упорядоченная тройка ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Любой вектор пространства единственным образом может быть разложен по базисным векторам, т.е. представлен в виде

где – координаты вектора в базисе 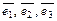(записывают: ).

В пространстве линейная независимость векторов равносильна их некомпланарности, т.е. любые три некомпланарных вектора, взятые в определенном порядке, образуют базис.

Пусть задана тройка некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора 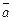до направления вектора , наблюдаемый с конца вектора совершается против часовой стрелки, то тройка векторов называется правой. В противном случае – левой. Всюду далее рассматриваются правые тройки базисных векторов.

Совокупность базисных векторов и их общего начала образуют, аффинную систему координат в пространстве. Координаты векторов в таком случае называют аффинными.

Если даны два вектора и в некотором базисе, то

тогда и только тогда, когда

(2)

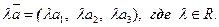(3)

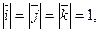
В случае, когда базисные векторы попарно перпендикулярны, система координат называется прямоугольной декартовой. Если добавить, кроме того, условие нормированности базисных векторов (т.е. их единичную длину), то такой базис называют ортонормированным и обозначают : 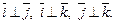Прямоугольные декартовы координаты вектора 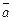является его проекциями на вектора соответственно.

Если точка M имеет прямоугольные декартовы координаты x, y, z в системе координат с началом в точке O(0, 0, 0) и базисом , то соответствующий радиус-вектор

Если 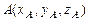и , то

.

Линейные операции для векторов и в координатной форме и их скалярное произведение вычисляются по формулам:

; (4)

(5)

(6)

; (7)

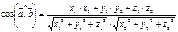. (8)

Направляющими косинусами вектора называются величины , где 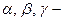углы, которые образует вектор соответственно с осями . Их вычисляют по формулам:

(9)

Если 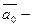единичный вектор, то .

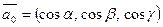Координаты точки C, делящей отрезок AB в отношении , можно найти по формулам:

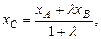
В.13 Векторное произведение

Векторным произведением 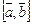двух векторов 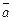и 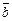называется вектор, удовлетворяющий следующим условиям:

1) ;

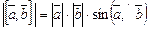2)

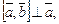
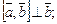
3) тройка векторов 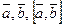– правая.

Векторное произведение обозначают также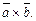

Если хотя бы один из векторов 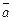или 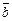нулевой, то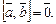

Геометрический смысл векторного произведения 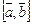состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах 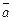и :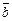

.

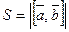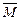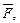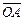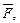Физический смысл векторного произведения состоит в том, что момент силы приложенной к точке A, относительно точки O есть векторное произведение векторов и т. е.

.

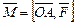Свойства векторного произведения:

1) ;

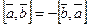2) ;

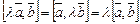3) ;

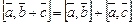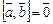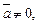
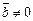4) при тогда и только тогда, когда векторы 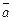и 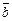коллинеарны.

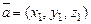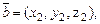Если и то

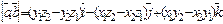
Последнюю формулу удобно записать в виде формального определения третьего порядка:

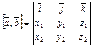
В.14. Смешанное произведение векторов

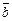Смешанным произведением трех векторов и 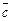называется число, определяемое соотношением

.

Если хотя бы один из векторов 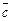– нулевой, то их смешанное произведение равно нулю.

Геометрический смысл смешанного произведения векторов 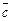состоит в том, что его абсолютное значение равно объему V параллелепипеда, построенного на векторах приведенных к общему началу:

.

Свойства смешанного произведения

1) ;

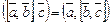2) ;

;

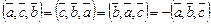3) , где

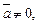
4) при тогда и только тогда, когда 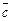– компланарные векторы;

5) векторы 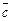образуют базис в трехмерном пространстве при условии

6) если то векторы образуют правую тройку; если – левую.

В случае, когда векторы заданы в ортонормированном базисе координатами их смешанное произведение может быть найдено по формуле . (10)

Плоскость в пространстве

1. Положение плоскости P в пространстве относительно прямоугольной системы координат Oxyz однозначно определено, если задан радиус-вектор 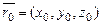некоторой фиксированной точки 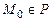и два некомпланарных вектора и , параллельных данной плоскости. В этом случае равенство 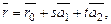где 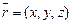– радиус-вектор произвольной точки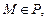 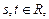называется векторно-параметрическим уравнением плоскости P. Записав его в координатной форме получим параметрические уравнения плоскости.

2. Эту же плоскость можно задать одним из уравнений:

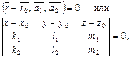(1)

справедливость которых обусловлена условием компланарности векторов 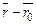, 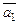и .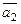

3. Координаты векторов 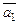и 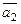могут быть найдены, если известны три точки плоскости P, не лежащие на одной прямой: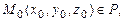

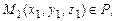
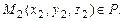
В этом случае 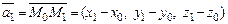, 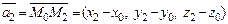. В результате имеем уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой.

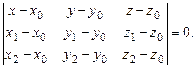
4. Если известны точки пересечения плоскости P с координатными осями, т. е. M₀(a, 0, 0), M₁(0, b, 0), M₂(0, 0, c), то справедливо уравнение «в отрезках»:

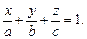
5. Положение плоскости P в пространстве однозначно определено и в том случае, когда задан нулевой нормальный вектор 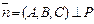и точка 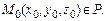Условия перпендикулярности векторов 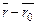и 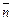позволят перейти к векторному уравнению 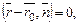а затем к его координатной форме записи:

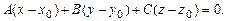(2)

После преобразования последнего уравнения приходим к общему уравнению плоскости P:

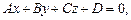где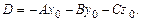

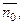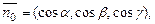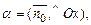
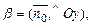
6. Если в качестве нормального вектора плоскости P взять единичный вектор направленный из начала координат в сторону плоскости, то где 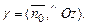Тогда справедливо нормальное уравнение плоскости

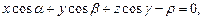
где 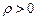– расстояние от начала координат до плоскости.

Величина 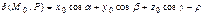, где 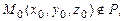называется отклонением точки 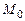от плоскости 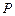. При этом 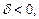если 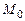и O(0, 0, 0) лежат по одну сторону от плоскости, 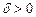– если лежат по разные, 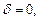если 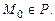Расстояние 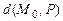от точки 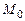до плоскости 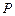равно абсолютному значению ее отклонения, т. е.

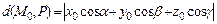.От общего уравнения плоскости к нормальному можно перейти с помощью умножения на нормирующий множитель

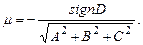
Значит, расстояние 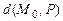от точки 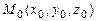до плоскости 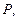заданной общим уравнением 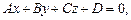может быть найдено по формуле

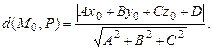
Угол 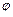между плоскостями в пространстве определяется по косинусу угла между нормальными векторам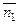и и 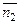этих плоскостей:

⇐ Предыдущая123456Следующая ⇒

Поделиться: