Работа в системе Microsoft Office Excel
Использование относительных, абсолютных и смешанных ссылок в формулах
Относительные ссылки. Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейку, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании относительной ссылки из ячейки B2 в ячейку B3, она автоматически изменяется с =A1 на =A2.
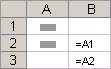
Скопированная формула с относительной ссылкой
Абсолютные ссылки. Абсолютная ссылка ячейки в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании формулы вдоль строк и вдоль столбцов абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, и для использования абсолютных ссылок надо выбрать соответствующий параметр. Например, при копировании абсолютной ссылки из ячейки B2 в ячейку B3, она остается прежней =$A$1.
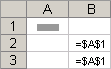
Скопированная формула с абсолютной ссылкой
Смешанные ссылки. Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка столбцов приобретает вид $A1, $B1 и т. д. Абсолютная ссылка строки приобретает вид A$1, B$1 и т. д. При изменении позиции ячейки, содержащей формулу, относительная ссылка изменяется, а абсолютная ссылка не изменяется. При копировании формулы вдоль строк и вдоль столбцов относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании смешанной ссылки из ячейки A2 в ячейку B3, она изменяется с =A$1 на =B$1.
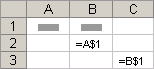
Таблица 3.1
| Примеры использования относительной и абсолютной адресации
| | | 1, 111
| 5, 556
| 6, 667
| ← A2+B2
|
| | | 1, 836
| 4, 028
| 5, 864
| ← A3+B3
|
| | | 2, 561
| 2, 920
| 5, 481
| ← A4+B4
|
| | | 3, 286
| 2, 117
| 5, 403
| ← A5+B5
|
| | | 4, 011
| 1, 535
| 5, 546
| ← A6+B6
|
| | |
|
|
|
|
| | | Пример использования абсолютной адресации
|
| | |
|
|
|
|
| | | Константа =
| 3, 14159
|
|
|
| | | 0, 00100
| 0, 00314
| ← =$B$10*A11
|
| | | 0, 00700
| 0, 02199
| ← =$B$10*A12
|
| | | 0, 04900
| 0, 15394
| ← =$B$10*A13
|
| | | 0, 34300
| 1, 07757
| ← =$B$10*A14
|
| | | 2, 40100
| 7, 54296
| ← =$B$10*A15
|
| | | 16, 80700
| 52, 80075
| ← =$B$10*A16
|
| | |
|
|
|
|
| | | 27.12.2011
| вторник
| Вт
|
|
| | | 01.01.2012
| воскресенье
| Вс
|
| | |
3.2 Построение графиков функций (с заданием исходных данных Xn, Xk и N )
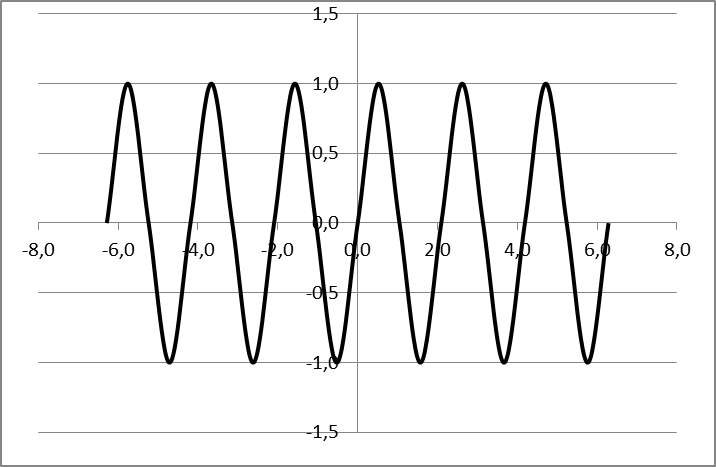
3.2.1
| График функции
|
| | | Исходные данные
| | | | Xнач=
| -6, 283
| | | | Xкон=
| 6, 283
| | | | Nx=
|
| | | | Hx=
| 0, 524
| | | | a=
| 1, 22
| | | | b=
|
| | |
| Расчётные значения
| | x
| y
| | -6, 283
| 0, 000
| | -5, 760
| 1, 000
| | -5, 236
| 0, 000
| | -4, 712
| -1, 000
| | -4, 189
| 0, 000
| | -3, 665
|  1, 000 1, 000
| | -3, 142
| 0, 000
| | -2, 618
| -1, 000
| | -2, 094
| 0, 000
| | -1, 571
| 1, 000
| | -1, 047
| 0, 000
| | -0, 524
| -1, 000
| | 0, 000
| 0, 000
| | 0, 524
| 1, 000
| | 1, 047
| 0, 000
| | 1, 571
| -1, 000
| | 2, 094
| 0, 000
| | 2, 618
| 1, 000
| | 3, 142
| 0, 000
| | 3, 665
| -1, 000
| | 4, 189
| 0, 000
| | 4, 712
| 1, 000
| | 5, 236
| 0, 000
| | 5, 760
| -1, 000
| | 6, 283
| 0, 000
|
3.2.2
| График функции
| | 𝑌 =𝑎 ∙ 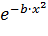
|
| | | Исходные данные
| | | | | Xнач=
| -6, 283
| | | | | Xкон=
| 6, 283
| | | | | Nx=
|
| | | | | Hx=
| 0, 524
| | | | | a=
| 1, 22
| | | | | b=
| 0, 25
| | | |
| Расчётные значения
| | x
| y
| | -6, 283
| 0, 000
| | -5, 759
| 0, 000
| | -5, 236
| 0, 001
| | -4, 712
| 0, 005
| | -4, 189
| 0, 015
| | -3, 665
| 0, 042
| | -3, 142
|  0, 103 0, 103
| | -2, 618
| 0, 220
| | -2, 094
| 0, 408
| | -1, 571
| 0, 658
| | -1, 047
| 0, 927
| | -0, 524
| 1, 139
| | 0, 000
| 1, 220
| | 0, 524
| 1, 139
| | 1, 047
| 0, 927
| | 1, 571
| 0, 658
| | 2, 094
| 0, 408
| | 2, 618
| 0, 220
| | 3, 142
| 0, 103
| | 3, 665
| 0, 042
| | 4, 189
| 0, 015
| | 4, 712
| 0, 005
| | 5, 236
| 0, 001
| | 5, 759
| 0, 000
| | 6, 283
| 0, 000
| | 6, 807
| 0, 000
| | 7, 330
| 0, 000
|
3.2.3
| График функции
|
| | | | | | | | | | Исходные данные
| | | Xнач=
| -1
| | | Xкон=
|
| | | Nx=
|
| | | Hx=
| 0, 083
| | | a=
| 1, 22
| | | b=
| 0, 25
| |
| Расчётные значения
| | x
| y
| | 0, 000
| 1, 000
| | 0, 083
| 1, 181
| | 0, 167
| 1, 396
| | 0, 250
|  1, 649 1, 649
| | 0, 333
| 1, 948
| | 0, 417
| 2, 301
| | 0, 500
| 2, 718
| | 0, 583
| 3, 211
| | 0, 667
| 3, 794
| | 0, 750
| 4, 482
| | 0, 833
| 5, 294
| | 0, 917
| 6, 255
| | 1, 000
| 7, 389
| | 1, 083
| 8, 729
| | 1, 167
| 10, 312
| | 1, 250
| 12, 182
| | 1, 333
| 14, 392
| | 1, 417
| 17, 002
| | 1, 500
| 20, 086
| | 1, 583
| 23, 728
| | 1, 667
| 28, 032
| | 1, 750
| 33, 115
| | 1, 833
| 39, 121
| | 1, 917
| 46, 216
| | 2, 000
| 54, 598
| | 2, 083
| 64, 500
| | 2, 167
| 76, 198
|
| 3.2.4 График функции
|
| 
| | Исходные данные
| | | Xнач=
|
| | | Xкон=
|
| | | Yнач=
|
| | | Yкон=
|
| | | Nx=
|
| | | Hx=
| 21, 429
| | | a=
| 1, 22
| | | b=
| 0, 25
| |
| X
| Y
| |
| 0, 00
| 21, 43
| 42, 86
| 64, 29
| 85, 71
| 107, 14
| 128, 57
| 150, 00
| 171, 43
| 192, 86
| 214, 29
| 235, 71
| 257, 14
| 278, 57
| 300, 00
| |
| 0, 00
| -4, 63
| -6, 55
| -8, 02
| -9, 26
| -10, 35
| -11, 34
| -12, 25
| -13, 09
| -13, 89
| -14, 64
| -15, 35
| -16, 04
| -16, 69
| -17, 32
| | 21, 43
| 4, 63
| 0, 00
| -1, 92
| -3, 39
| -4, 63
| -5, 72
| -6, 71
| -7, 62
| -8, 46
| -9, 26
| -10, 01
| -10, 72
| -11, 41
| -12, 06
| -12, 69
| | 42, 86
| 6, 55
| 1, 92
| 0, 00
| -1, 47
| -2, 71
| -3, 80
| -4, 79
| -5, 70
| -6, 55
| -7, 34
| -8, 09
| -8, 81
| -9, 49
| -10, 14
| -10, 77
| | 64, 29
| 8, 02
| 3, 39
| 1, 47
| 0, 00
| -1, 24
| -2, 33
| -3, 32
| -4, 23
| -5, 08
| -5, 87
| -6, 62
| -7, 34
| -8, 02
| -8, 67
| -9, 30
| | 85, 71
| 9, 26
| 4, 63
| 2, 71
| 1, 24
| 0, 00
| -1, 09
| -2, 08
| -2, 99
| -3, 83
| -4, 63
| -5, 38
| -6, 09
| -6, 78
| -7, 43
| -8, 06
| | 107, 14
| 10, 35
| 5, 72
| 3, 80
| 2, 33
| 1, 09
| 0, 00
| -0, 99
| -1, 90
| -2, 74
| -3, 54
| -4, 29
| -5, 00
| -5, 68
| -6, 34
| -6, 97
| | 128, 57
| 11, 34
| 6, 71
| 4, 79
| 3, 32
| 2, 08
| 0, 99
| 0, 00
| -0, 91
| -1, 75
| -2, 55
| -3, 30
| -4, 01
| -4, 70
| -5, 35
| -5, 98
| | 150, 00
| 12, 25
| 7, 62
| 5, 70
| 4, 23
| 2, 99
| 1, 90
| 0, 91
| 0, 00
| -0, 85
| -1, 64
| -2, 39
| -3, 11
| -3, 79
| -4, 44
| -5, 07
| | 171, 43
| 13, 09
| 8, 46
| 6, 55
| 5, 08
| 3, 83
| 2, 74
| 1, 75
| 0, 85
| 0, 00
| -0, 79
| -1, 55
| -2, 26
| -2, 94
| -3, 60
| -4, 23
| | 192, 86
| 13, 89
| 9, 26
| 7, 34
| 5, 87
| 4, 63
| 3, 54
| 2, 55
| 1, 64
| 0, 79
| 0, 00
| -0, 75
| -1, 47
| -2, 15
| -2, 80
| -3, 43
| | 214, 29
| 14, 64
| 10, 01
| 8, 09
| 6, 62
| 5, 38
| 4, 29
| 3, 30
| 2, 39
| 1, 55
| 0, 75
| 0, 00
| -0, 71
| -1, 40
| -2, 05
| -2, 68
| | 235, 71
| 15, 35
| 10, 72
| 8, 81
| 7, 34
| 6, 09
| 5, 00
| 4, 01
| 3, 11
| 2, 26
| 1, 47
| 0, 71
| 0, 00
| -0, 68
| -1, 34
| -1, 97
| | 257, 14
| 16, 04
| 11, 41
| 9, 49
| 8, 02
| 6, 78
| 5, 68
| 4, 70
| 3, 79
| 2, 94
| 2, 15
| 1, 40
| 0, 68
| 0, 00
| -0, 65
| -1, 28
| | 278, 57
| 16, 69
| 12, 06
| 10, 14
| 8, 67
| 7, 43
| 6, 34
| 5, 35
| 4, 44
| 3, 60
| 2, 80
| 2, 05
| 1, 34
| 0, 65
| 0, 00
| -0, 63
| | 300, 00
| 17, 32
| 12, 69
| 10, 77
| 9, 30
| 8, 06
| 6, 97
| 5, 98
| 5, 07
| 4, 23
| 3, 43
| 2, 68
| 1, 97
| 1, 28
| 0, 63
| 0, 00
|
3.3 Расчет материального баланса
Таблица 3.1 - Исходные данные узла сепарации
| Наименование показателя
| Условные обозначе ния
| Единиы измере ния
| Величина
| Обоснование
| | Поступающий поток
| G1
| т/ч
|
| с узла ферментации
| | Концентрация суспензии в потоках
|
|
|
|
| | - поступающий
| X1
| г/л
|
| с узла ферментации
| | - сконцентрированный
| X2
| г/л
|
| принимаем
| | - очищенный
| X3
| г/л
|
| принимаем
| Примечание. Концентрация для суспензии задана в г/л в расчете на суспензию с влажностью 75%
|
|
|
|
|
|
|
|
| |
| G1=
|
|
|
|
|
|
| |
| X1=
| 140
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
| G2=
| ?
|
|
| |
|
|
|
| X2=
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
| G3=
| ?
|
|
| |
|
|
|
| X3=
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| | Система уравнений материального баланса
|
| Решение системы методом подстановки
|
| |
| G3=G1-G2
| 
|
| =
| 3, 812
| | G1*X1=G2*X2+G3*X3
| G1*(X1-X2)=G2*(X2-X3)
|
|
|
Таблица 3.2 - Материальный баланс узла сепарации
| Приход
| Расход
| | Наименование потока
| Всего
| В
т.ч тв.фаза
| Наименование потока
| Всего
| В
т.ч. Тв.фаза
| | - поступающий
|
| 0, 525
| - сконцентрированный
| 3, 812
| 0, 519
| | - очищенный
| 11, 188
| 0, 006
| | Итого
|
| 0, 525
| Итого
|
| 0, 525
|
3.4 Решение системы линейных уравнений матричным методом
2X1-4X2-2X3=2
-0, 12 X1-2 X2+3 X3=3
3 X1+1, 5 X2-5 X3=4
Таблица 3.3 – Матрица
| A
| | 2, 00
| -4, 00
| -2, 00
| | -0, 12
| -2, 00
| 3, 00
| | 3, 00
| 1, 50
| -5, 00
| Таблица 3.4 – Обратная матрица
| A-1
| | -0, 16
| 0, 67
| 0, 47
| | -0, 25
| 0, 12
| 0, 17
| | -0, 17
| 0, 44
| 0, 13
| X=A-1B
Таблица 3.5 – Решение системы
| Решение системы
|
| | X1
| 4, 206
| | X2
| 1, 514
| | X3
| 2, 178
|
Работа с базами данных в системе Microsoft Office Access
|

