Собственные значения матрицы
| N° [orig]
| Кол-во верных ответов:
| Вопрос:
| Варианты ответов
| | 1 [0]
|
| Собственные значения собственных векторов линейного преобразования, заданного в некотором базисе матрицей 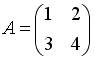 , могут быть найдены по формуле… , могут быть найдены по формуле…
| 1 )  2 )
2 )  3 )
3 ) 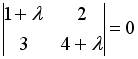 4 )
4 ) 
| | 2 [14]
|
| Вектор  является собственным вектором матрицы А, соответствующий собственному значению является собственным вектором матрицы А, соответствующий собственному значению  . Тогда произведение . Тогда произведение  равно … равно …
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 
| | 3 [23]
|
| Вектор  является собственным вектором матрицы является собственным вектором матрицы  . Тогда соответствующее собственное значение равно … . Тогда соответствующее собственное значение равно …
| 1 )4
2 )− 3
3 )1
4 )- 1
| | 4 [26]
|
| Вектор  является собственным вектором матрицы является собственным вектором матрицы  . Тогда соответствующее собственное значение равно … . Тогда соответствующее собственное значение равно …
| 1 )- 1
2 )5
3 )2
4 )- 2
| | 5 [30]
|
| Вектор 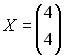 является собственным вектором матрицы является собственным вектором матрицы  . Тогда соответствующее собственное значение равно … . Тогда соответствующее собственное значение равно …
| 1 )- 5
2 )0
3 )1
4 )5
| | 6 [32]
|
| Вектор 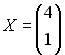 является собственным вектором матрицы является собственным вектором матрицы  . Тогда соответствующее собственное значение равно … . Тогда соответствующее собственное значение равно …
| 1 )1
2 )- 5
3 )6
4 )- 6
| Системы линейных уравнений: основные понятия
| N° [orig]
| Кол-во верных ответов:
| Вопрос:
| Варианты ответов
| | 1 [0]
|
| В системе уравнений  независимыми (свободными) переменными можно считать… независимыми (свободными) переменными можно считать…
| 1 )  , ,  , ,  , ,  , ,  2 )
2 )  3 )
3 )  4 )
4 )  , ,  , , 
| | 2 [4]
|
| В системе уравнений  независимыми (свободными) переменными можно считать… независимыми (свободными) переменными можно считать…
| 1 )  , ,  , ,  2 )
2 )  3 )
3 )  4 )
4 ) 
| | 3 [5]
|
| В системе уравнений  независимыми (свободными) переменными можно считать… независимыми (свободными) переменными можно считать…
| 1 )  , ,  , ,  2 )
2 )  3 )
3 )  4 )
4 )  , ,  , ,  , ,  , , 
| | 4 [7]
|
| В системе уравнений  базисными (несвободными) переменными можно считать… базисными (несвободными) переменными можно считать…
| 1 )  , ,  , ,  2 )
2 )  , ,  , ,  , ,  , ,  3 )
3 )  , ,  4 )
4 ) 
| | 5 [8]
|
| В системе уравнений 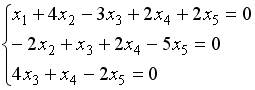 базисными (несвободными) переменными можно считать… базисными (несвободными) переменными можно считать…
| 1 )  2 )
2 )  , ,  3 )
3 )  , ,  , ,  4 )
4 )  , , 
| | 6 [9]
|
| В системе уравнений  базисными (несвободными) переменными можно считать… базисными (несвободными) переменными можно считать…
| 1 )  , ,  , ,  2 )
2 )  , ,  3 )
3 )  4 )
4 ) 
|
Квадратичные формы
| N° [orig]
| Кол-во верных ответов:
| Вопрос:
| Варианты ответов
| | 1 [0]
|
| Матрице 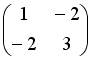 соответствует квадратичная форма … соответствует квадратичная форма …
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 
| | 2 [2]
|
| Матрице  соответствует квадратичная форма … соответствует квадратичная форма …
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 
| | 3 [3]
|
| Матрице  соответствует квадратичная форма … соответствует квадратичная форма …
| 1 )  2 )
2 )  3 )
3 ) 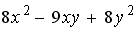 4 )
4 ) 
| | 4 [7]
|
| Матрице  соответствует квадратичная форма … соответствует квадратичная форма …
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 
| | 5 [9]
|
| Матрице  соответствует квадратичная форма … соответствует квадратичная форма …
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 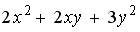
| | 6 [10]
|
| Матрице 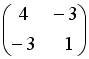 соответствует квадратичная форма … соответствует квадратичная форма …
| 1 )  2 )
2 ) 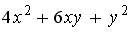 3 )
3 )  4 )
4 ) 
| Функции: основные понятия и определения
| N° [orig]
| Кол-во верных ответов:
| Вопрос:
| Варианты ответов
| | 1 [0]
|
| Дана функция  . Тогда ее областью значений является множество… . Тогда ее областью значений является множество…
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 
| | 2 [13]
|
| Наименьшее целое значение x из области определения функции  равно… равно…
| 1 )2
2 )3
3 )4
4 )5
| | 3 [22]
|
| Наименьшее значение  из области значений функции из области значений функции 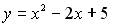 равно… равно…
| 1 )3
2 )4
3 )6
4 )5
| | 4 [26]
|
| Наименьшее значение  из области значений функции из области значений функции  равно… равно…
| 1 )– 3
2 )9
3 )– 12
4 )– 6
| | 5 [32]
|
| Наименьшее значение  из области значений функции из области значений функции  равно… равно…
| 1 )- 44
2 )- 12
3 )20
4 )4
| | 6 [43]
|
| Дана функция  . Тогда ее областью определения является множество … . Тогда ее областью определения является множество …
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 
|
Непрерывность функции. Точки разрыва
| N° [orig]
| Кол-во верных ответов:
| Вопрос:
| Варианты ответов
| | 1 [0]
|
| Число точек разрыва функции  равно… равно…
| 1 )3
2 )1
3 )0
4 )2
| | 2 [2]
|
| Число точек разрыва функции  равно… равно…
| 1 )3
2 )2
3 )8
4 )4
| | 3 [3]
|
| Число точек разрыва функции  равно… равно…
| 1 )3
2 )0
3 )5
4 )2
| | 4 [7]
|
| Число точек разрыва функции  равно… равно…
| 1 )4
2 )3
3 )7
4 )0
| | 5 [9]
|
| Число точек разрыва функции 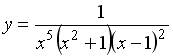 равно… равно…
| 1 )2
2 )3
3 )7
4 )9
| | 6 [10]
|
| Число точек разрыва функции  равно… равно…
| 1 )3
2 )1
3 )0
4 )2
|
Производные первого порядка
| N° [orig]
| Кол-во верных ответов:
| Вопрос:
| Варианты ответов
| | 1 [0]
|
| Установите соответствие между функцией и ее производной: 1.  2. 2.  3. 3. 
| 1 ) 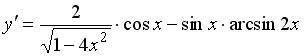 2 )
2 )  3 )
3 )  4 )
4 )  5 )
5 ) 
| | 2 [2]
|
| Установите соответствие между функцией и ее производной: 1.  2. 2.  3. 3. 
| 1 )  2 )
2 )  3 )
3 )  4 )
4 )  5 )
5 ) 
| | 3 [3]
|
| Установите соответствие между функцией и ее производной: 1.  2. 2.  3. 3. 
| 1 ) 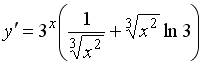 2 )
2 )  3 )
3 )  4 )
4 )  5 )
5 ) 
| | 4 [7]
|
| Установите соответствие между функцией и ее производной: 1.  2. 2.  3. 3. 
| 1 )  2 )
2 ) 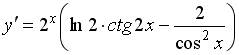 3 )
3 )  4 )
4 )  5 )
5 ) 
| | 5 [9]
|
| Установите соответствие между функцией и ее производной: 1.  2. 2.  3. 3. 
| 1 ) 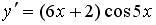 2 )
2 )  3 )
3 )  4 )
4 )  5 )
5 ) 
| | 6 [10]
|
| Установите соответствие между функцией и ее производной: 1.  2. 2.  3. 3. 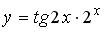
| 1 )  2 )
2 ) 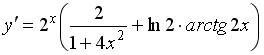 3 )
3 )  4 )
4 )  5 )
5 ) 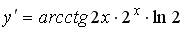
|
Производные высших порядков
| N° [orig]
| Кол-во верных ответов:
| Вопрос:
| Варианты ответов
| | 1 [0]
|
| Значение производной второго порядка функции 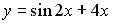 в точке в точке 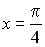 равно… равно…
| 1 )- 4
2 )- 1
3 )1
4 )4
| | 2 [4]
|
| Значение производной второго порядка функции  в точке в точке  равно… равно…
| 1 )- 11
2 )- 10
3 )- 12
4 )- 1
| | 3 [8]
|
| Значение производной второго порядка функции  в точке в точке  равно … равно …
| 1 )9
2 )1
3 )0
4 )6
| | 4 [9]
|
| Значение производной второго порядка функции 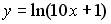 в точке в точке  равно … равно …
| 1 )- 100
2 )100
3 )- 1
4 )1
| | 5 [14]
|
| Производная второго порядка функции  имеет вид… имеет вид…
| 1 )  2 )
2 ) 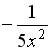 3 )
3 )  4 )
4 ) 
| | 6 [15]
|
| Производная второго порядка функции  имеет вид… имеет вид…
| 1 )  2 )
2 )  3 )
3 )  4 )
4 ) 
|
Асимптоты графика функции
|

