Интервалы монотонности функции. Экстремумы функции. Наибольшее и наименьшее значения функции.
Выпуклость и вогнутость. Точки перегиба.
Студент должен:
Знать:
- Понятия возрастающей и убывающей функций;
- Признаки монотонности функции;
- Алгоритм нахождения интервалов монотонности;
- Понятие экстремума функция;
- Признаки экстремума функции;
- Алгоритм исследования функции на экстремум;
- Понятия наибольшего и наименьшего значений функции на отрезке
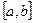 ;
; - Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке
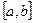 ;
; - Понятии выпуклой и вогнутой функций4
- Алгоритм нахождения интервалов выпуклости и вогнутости функции;
- Понятие точки перегиба;
- Алгоритм нахождения точек перегиба.
Уметь:
- Исследовать функцию на монотонность и экстремумы с помощью 1-ой и 2-ой производной;
- Находить наибольшее и наименьшее значения функции на отрезке
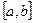 ;
;
- Находить интервалы выпуклости и вогнутости функции;
- Находить точки перегиба функции.
Содержание:
- Возрастающая и убывающая функция;
- Признаки монотонности функции;
- Алгоритм нахождения интервалов монотонности;
- Понятие экстремума функция;
- Признаки экстремума функции (необходимый и достаточный);
- Алгоритм исследования функции на экстремум;
- Исследование функций на монотонность и экстремумы с помощью производной;
- Наибольшее и наименьшее значения функции на отрезке
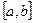 ;
; - Интервалы выпуклости и вогнутости функции;
- Точки перегиба функции.
Асимптоты графика функции. Полное исследование функции.
Студент должен:
Знать:
- Понятие асимптоты графика функции;
- Виды асимптот;
- Формулы асимптот: вертикальной, горизонтальной и наклонной;
- Алгоритм полного исследования функции.
Уметь:
- Находить асимптоты графика функции: вертикальную, горизонтальную и наклонную;
- Исследовать функцию и строить её график по результатам исследования.
Содержание:
- Асимптоты графика функции;
- Вертикальная асимптота;
- Горизонтальная асимптота;
- Наклонная асимптота;
- Алгоритм полного исследования функции.
Контрольные вопросы:
Дифференциальное исчисление функции одной действительной переменной.
- Производная функции. Производные основных элементарных функций. Производная сложной функции.
- Дифференциал функции. Применение дифференциала в приближённых вычислениях.
- Интервалы возрастания и убывания функции. Экстремумы функции.
- Наибольшее и наименьшее значения функции.
- Выпуклость и вогнутость. Точки перегиба.
- Асимптоты графика функции.
- Полное исследование функции и построение её графика.
Интегральное исчисление функции одной
Действительной переменной.
Первообразная функции. Неопределённый интеграл и его свойства. Непосредственное интегрирование.
Студент должен:
Знать:
- Понятие первообразной функции;
- Понятие неопределённого интеграла;
- Свойства неопределённого интеграла;
- Основные формулы интегрирования.
Уметь:
- Находить первообразную функции;
- Находить неопределённые интегралы, сводящиеся к табличным с помощью основных свойств и простейших преобразований.
Содержание:
- Первообразная функции и её неоднозначность;
- Неопределённый интеграл;
- Его свойства;
- Основные формулы интегрирования;
- Нахождение неопределённых интегралов.
Метод подстановки, метод интегрирования по частям в неопределённом интеграле. Интегрирование рациональных дробей.
Студент должен:
Знать:
- Свойства неопределённого интеграла;
- Основные формулы интегрирования;
- Метод интегрирования по частям;
- Понятие простейшей, рациональной дроби;
- Четыре случая метода интегрирования рациональных дробей.
Уметь:
- Находить неопределённые интегралы, используя метод подстановки.
- Находить неопределённые интегралы, используя метод интегрирования по частям.
- Находить неопределённые интегралы, используя метод рациональных дробей.
Содержание:
- Метод интегрирования по частям;
- Метод рациональных дробей (4 случая, исчерпывающие все возможные варианты);
- Нахождение неопределённых интегралов, используя метод подстановки, используя метод интегрирования по частям, интегрирование методом рациональных дробей.

