
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
I. Система двух линейных уравнений с двумя неизвестнымиСтр 1 из 3Следующая ⇒
I. Система двух линейных уравнений с двумя неизвестными Систем двух линейных уравнений с двумя неизвестными имеет вид
Определителем этой системы называется определитель, составленный из коэффициентов при неизвестных. Этот определитель
будем обозначать буквой D. 1. Если определитель системы не равен нулю, то система (4) имеет единственное решение, которое находится по формулам
В этом случае говорят, что система - совместная или определенная. Определители, стоящие в числителях этих дробей, будем обозначать соответственно через Dx и Dy. Итак, значение неизвестного системы (4) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов. 2. Если же определитель системы D равен нулю, но, по крайней мере, один из определителей Dx и Dy в числителях формул (6) не равен нулю, то система решений не имеет. В этом случае говорят, что она противоречива, или несовместна. 3. Если же равен нулю не только определитель системы, но и определители Dx и Dy, а хотя бы один из коэффициентов при неизвестных не равен нулю, то одно из уравнений системы является следствием другого, и система (4) двух линейных уравнений с двумя неизвестными приводится к одному уравнению, всякое решение которого является одновременно и решением второго уравнения. В этом случае система допускает бесконечное множество решений, и о ней говорят, что она неопределенная. II. Система трех линейных уравнений с тремя неизвестными Система трех линейных уравнений с тремя неизвестными имеет вид
Определитель
составленный из коэффициентов при неизвестных, называется определителем системы. 1. Если определитель системы
Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов. Определители, стоящие в числителях дробей (9), будем обозначать соответственно через Dx, Dy, Dz. 2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей Dx, Dy и Dz не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна. 3. Если D = 0 и все определители, стоящие в числителях дробей (9), - Dx, Dy, Dz - равны нулю, т. е. если D = Dx = Dy = Dz = 0, но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной. 4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей Dx, Dy, Dz не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет. 5. Если в определителях D, Dx, Dy, Dz все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям. Линейные операции с векторами на плоскости и в пространстве. Линейными операциями над векторам называются операции сложения векторов и умножения вектора на число. Уравнение плоскости 1)Ax+By+Cz+D=0 A2+B2+C2≠ 0 Общее уравнение плоскости.(А, В, С)- вектор, перпендикулярный плоскости 2) А(x-x0)+B(y-y0)+C(z-z0)=0 A2+B2+C2≠ 0 Уравнение плоскости по точке (x0, y0, z0) b jhnjujyfkmyjve dtrnjhe (A, B, C) 3)z=kxx+kyy+b Уравнение плоскост с угловыми коэффициентами kx и ky 4) a≠ 0, b≠ 0, c≠ 0 Уравнение плоскости в отрезках a, b, c 5) x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 =0 Уравнение плоскости по трем точкам (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) x3-x1 y3-y1 z3-z1
Эллипс Эллипс – это множество точек, сумма расстояний от которых до 2 – х заданных точек есть величина постоянная. Сами эти 2 точки наз – ся фокальными точками или фокусом эллипса. Прямая которая проходит через фокальную точку наз – ся большой осью эллипса. Прямая перпендикулярная большой оси и проходящая через середину отрезка наз – ся малой осью эллипса. Свойства. 1)
2) Эллипс симетричен относительно оси и относительно началу координат. 3)
4)
Уравнение касательной к эллипсу x*x0/ a2 + y* y0/ b2 = 1
Гипербола
a2 b2
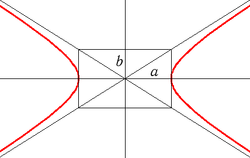 y2 x2 y2 x2
b2 a2
Линиями второго порядка называются линии, уравнения которых имеют вторую степень.
Парабола Параболой называется множество всех точек равноудалённых от данной точки (фокуса) и от данной прямой (директрисы).
Окружность Окружность- множество всех точек равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
№15 понятие функции одного аргумента и способы задания. Переменная величина называется функциией от переменной величины x, если они связаны между собой так, что каждому рассматриваемому значению величины x (допустимые значения) соответствует единственное вполне определенное значение у. Переменная х называется аргументом. Способы задания: 1)аналитический способ (если функция выражена при помощи формулы, то говорят, что она задана аналитически) 2) табичный способ 3)графический способ( соответствие между аргументом и функцией устанавливается с помощью графика)
№16 Основные элементарные функции 1)степенная функция y=xn 2)радикал y= 3)показательная функция Y=ax 4)логарифмическая функция Y=logax 5)тригонометрические функции Y=sinx y-cosx y=tgx y=ctgx
Обозначение предела функции Предел функции обозначается как
или через символ предела функции:
Свойства пределов функции 1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
2) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций. 3) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
21.
Приближенные вычисления Выполняя вычисления, всегда необходимо помнить о той точности, которую нужно или которую можно получить. Недопустимо вести вычисления с большой точностью, если данные задачи не допускают или не требуют этого (например, семизначная таблица логарифмов при вычислениях с числами, имеющими 5 верных значащих цифр - избыточна). Твёрдое знакомство с правилами приближенных вычислений необходимо каждому, кому приходится вычислять. Погрешности Разница между точным числом x и его приближенным значением a называется погрешностью данного приближенного числа. Если известно, что | x - a | < Da, то величина Da называется предельной абсолютной погрешностью приближенной величины a. Отношение Da / a = da называется предельной относительной погрешностью; последнюю часто выражают в процентах. Пример: 3, 14 является приближенным значением числа p, погрешность его равна 0, 00159..., предельную абсолютную погрешность можно считать равной 0, 0016, а предельную относительную погрешность v равной 0.0016/3.14 = 0, 00051 = 0, 051%. Для краткости обычно слово? предельная¦ опускается. Значащие цифры Если абсолютная погрешность величины a не превышает одной единицы разряда последней цифры числа a, то говорят, что у числа все знаки верные. Приближенные числа следует записывать, сохраняя только верные знаки. Если, например, абсолютная погрешность числа 52400 равна 100, то это число должно быть записано, например, в виде 524.102 или 0, 524.105. Оценить погрешность приближенного числа можно, указав, сколько верных значащих цифр оно содержит. При подсчете значащих цифр не считаются нули с левой стороны числа. Примеры: 1 куб.фут = 0.0283 м3 - три верных значащих цифры 1 дюйм = 2, 5400 v пять верных значащих цифр. Если число a имеет n верных значащих цифр, то его относительная погрешность da T 1/(z*dn-1), где z - первая значащая цифра числa a; d - основание системы счисления. У числа a с относительной погрешностью da верны n значащих цифр, где n - наибольшее целое число, удовлетворяющее неравенству (1+Z)da T dl-n. Пример: Если число a = 47, 542 получено в результате действий над приближенными числами и известно, что da = 0, 1%, то a имеет 3 верных знака, так как (4+1)0, 001 T 10v2. Округление Если приближенное число содержит лишние (или неверные) знаки, то его следует округлить. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем если первая отбрасываемая цифра больше или равна d/2, то последняя сохраняемая цифра увеличивается на единицу. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры округленного числа. Поэтому, чтобы после округления все знаки были верны, погрешность до округления должна быть не больше половины единицы того разряда, до которого предполагают делать округление.
Приближенное интегрирование Приближенное интегрирование – раздел вычислительной математики, занимающийся приближенным решением дифференциальных уравнений. Первой задачей приближенного интегрирования является приближенное вычисление интегралов (оно соответствует решению простейшего обыкновенного дифференциального уравнения y'=f(x)). В тех случаях, когда точное интегрирование невозможно (интеграл не может быть выражен в известных функциях), применяются аналитические методы приближенного интегрирования, заключающиеся в том, что подынтегральная функция заменяется другой, интеграл от которой вычисляется более или менее легко. В качестве такой функции часто берут интерполяционный многочлен. Приближенное интегрирование применяется также в тех случаях, когда интегрируемая функция задана таблицей или графиком или если она быстрее, чем интерполяционный многочлен, приводит к цели (с заданной точностью). Тогда применяют и графические методы (построение графика первообразной функции по графику подынтегральной функции, а также различные математические машины и приборы – вычислительные машины, интеграторы, планиметры и т.п.). Основной задачей приближенного интегрирования является приближенное решение дифференциальных уравнений весьма общего вида. Здесь также существуют как аналитические, так и численные методы решения задач.
Дополнительный вопрос Правила интегрирования. 1)∫ d(f(x))=f(x)+C; 2)d∫ f(x)dx=f(x)dx; 3)∫ kf(x)dx=kf(x)dx, где k — постоянная величина; 4)∫ (f(x))±g(x))dx=∫ f(x)dx±∫ g(x)dx; 5)∫ udv=uv-∫ vdu (интегрирование по частям); 6)∫ f(x)dx=F(x)+C 7) ∫ f(x)dx=F(x)+C 7.таблица неопределенных интегралов · ∫ xndx=xn+1/(n+1)+C, n · ∫ dx/x=lnІxІ+C · ∫ axdx =ax/lna + C · ∫ exdx=ex+C · ∫ sinxdx=-cosx +C · ∫ cosxdx=sinx +C · ∫ dx/cos2x=tgx+C · ∫ dx/sin2x=-ctgx +C · ∫ dx/(1+x2)=arctgx+C · или ∫ dx/(1+x2) =-arcctgx+C · ∫ dx/ · или ∫ dx/ · ∫ dx/(a2+x2)= · ∫ dx/(a2+x2)=- · ∫ dx/ · ∫ dx/ · ∫ dx/ Таблица производных
8. ДОПОЛНИТЕЛЬНЫЙ Формула Ньютона-Лейбница Если
ЭТО ЕСЛИ ВСЕ РАСПИСАТЬ: Если функция f (x) интегрируема на [a; b], то для любого
который называется интегралом с переменным верхним пределом. Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке. Если функция f интегрируема на [a; b] и непрерывна в
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.
Одним из основных результатов математического анализа является теорема Ньютона – Лейбница: Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a). Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β ],
Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:
Эллипс(основной 11)
12)Гипербола
a2 b2
 y2 x2 y2 x2
b2 a2
Линиями второго порядка называются линии, уравнения которых имеют вторую степень. Парабола Параболой называется множество всех точек равноудалённых от данной точки (фокуса) и от данной прямой (директрисы).
Окружность Окружность- множество всех точек равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
I. Система двух линейных уравнений с двумя неизвестными Систем двух линейных уравнений с двумя неизвестными имеет вид
Определителем этой системы называется определитель, составленный из коэффициентов при неизвестных. Этот определитель
будем обозначать буквой D. 1. Если определитель системы не равен нулю, то система (4) имеет единственное решение, которое находится по формулам
В этом случае говорят, что система - совместная или определенная. Определители, стоящие в числителях этих дробей, будем обозначать соответственно через Dx и Dy. Итак, значение неизвестного системы (4) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов. 2. Если же определитель системы D равен нулю, но, по крайней мере, один из определителей Dx и Dy в числителях формул (6) не равен нулю, то система решений не имеет. В этом случае говорят, что она противоречива, или несовместна. 3. Если же равен нулю не только определитель системы, но и определители Dx и Dy, а хотя бы один из коэффициентов при неизвестных не равен нулю, то одно из уравнений системы является следствием другого, и система (4) двух линейных уравнений с двумя неизвестными приводится к одному уравнению, всякое решение которого является одновременно и решением второго уравнения. В этом случае система допускает бесконечное множество решений, и о ней говорят, что она неопределенная. |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 537; Нарушение авторского права страницы