
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Или из покоординатной записи.
7. В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система координат; координаты обычно обозначаются латинскими буквами x, y, z и называются, соответственно, абсциссой, ординатой и аппликатой. Координатная ось OX называется осью абсцисс, ось OY – осью ординат, ось OZ – осью аппликат. Положительные направления отсчета по каждой из осей обозначаются стрелками. 8. Уравнение прямой на плоскости 1) Ax + By+ C = 0 – Общее уравн – е прямой 2) x/a + b/y = 1, где а и b не равны 0. – Уравн –е прямой в отрезка (a, b) 3) x – x0/ a = y – y0/b – Уравн – е прямой по точке (x0, y0 ) и направляющему вектору (a, b) 4) X = x0 + at Y = y0 + bt, - параметрическое уравн – е прямой
Уравнение прямой в пространстве 1) А1х + В1у + С1z + D1 = 0, где A2 + B2 + C2 не равны 0 – Общее уравнение прямой в пространстве. А2х + B2y + C2z + D2 = 0(2 уравнения в системе идут) 2) х – х0/a = y – y0/b = z – z0/c, где a, b, c не равны 0 – Уравн-е прямой по точке (х0, y0, z0) и направляющему вектору (a, b, c) 3) x – x1/ x2 – x1= y – y1/ y2 – y1= z – z1/ z2 – z1, где х2 не равн х1, у2 не равн у1, z2 не равн z1 – Уравн –е прямой по 2 точкам (x1, y1, z1)и (x2, y2, z2) 4) X= x0 + at Y = y0 + bt Z = z0 + ct - Параметрическое уравнение прямой по точке (x0, y0, z0) и направляющему вектору(a, b, c)
Уравнение плоскости 1)Ax+By+Cz+D=0 A2+B2+C2≠ 0 Общее уравнение плоскости.(А, В, С)- вектор, перпендикулярный плоскости 2) А(x-x0)+B(y-y0)+C(z-z0)=0 A2+B2+C2≠ 0 Уравнение плоскости по точке (x0, y0, z0) b jhnjujyfkmyjve dtrnjhe (A, B, C) 3)z=kxx+kyy+b Уравнение плоскост с угловыми коэффициентами kx и ky 4) a≠ 0, b≠ 0, c≠ 0 Уравнение плоскости в отрезках a, b, c 5) x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 =0 Уравнение плоскости по трем точкам (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) x3-x1 y3-y1 z3-z1
Эллипс Эллипс – это множество точек, сумма расстояний от которых до 2 – х заданных точек есть величина постоянная. Сами эти 2 точки наз – ся фокальными точками или фокусом эллипса. Прямая которая проходит через фокальную точку наз – ся большой осью эллипса. Прямая перпендикулярная большой оси и проходящая через середину отрезка наз – ся малой осью эллипса. Свойства. 1)
2) Эллипс симетричен относительно оси и относительно началу координат. 3)
4)
Уравнение касательной к эллипсу x*x0/ a2 + y* y0/ b2 = 1
Гипербола
a2 b2
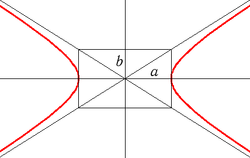 y2 x2 y2 x2
b2 a2
Линиями второго порядка называются линии, уравнения которых имеют вторую степень.
Парабола Параболой называется множество всех точек равноудалённых от данной точки (фокуса) и от данной прямой (директрисы).
Окружность Окружность- множество всех точек равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
№15 понятие функции одного аргумента и способы задания. Переменная величина называется функциией от переменной величины x, если они связаны между собой так, что каждому рассматриваемому значению величины x (допустимые значения) соответствует единственное вполне определенное значение у. Переменная х называется аргументом. Способы задания: 1)аналитический способ (если функция выражена при помощи формулы, то говорят, что она задана аналитически) 2) табичный способ 3)графический способ( соответствие между аргументом и функцией устанавливается с помощью графика)
№16 Основные элементарные функции 1)степенная функция y=xn 2)радикал y= 3)показательная функция Y=ax 4)логарифмическая функция Y=logax 5)тригонометрические функции Y=sinx y-cosx y=tgx y=ctgx
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине). Обозначение предела функции Предел функции обозначается как
или через символ предела функции:
Свойства пределов функции 1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
2) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций. 3) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
|
Последнее изменение этой страницы: 2017-03-14; Просмотров: 309; Нарушение авторского права страницы