
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Методы физического исследования: опыт, гипотеза, эксперимент, теорияСтр 1 из 19Следующая ⇒
Методы физического исследования: опыт, гипотеза, эксперимент, теория Нау́ чный ме́ тод — совокупность основных способов получения новых знаний и методов решения задач в рамках любой науки.Метод включает в себя способы исследования феноменов, систематизацию, корректировку новых и полученных ранее знаний. Умозаключения и выводы делаются с помощью правил и принципов рассуждения на основе эмпирических (наблюдаемых и измеряемых) данных об объекте. Базой получения данных являются наблюдения и эксперименты. Для объяснения наблюдаемых фактов выдвигаются гипотезы и строятся теории, на основании которых формулируются выводы и предположения. Полученные прогнозы проверяются экспериментом или сбором новых фактов. Важной стороной научного метода, его неотъемлемой частью для любой науки, является требование объективности, исключающее субъективное толкование результатов. Для обеспечения независимой проверки проводится документирование наблюдений, обеспечивается доступность для других учёных всех исходных данных, методик и результатов исследований. Это позволяет не только получить дополнительное подтверждение путём воспроизведения экспериментов, но и критически оценить степень адекватности (валидности) экспериментов и результатов по отношению к проверяемой теории. Существует четыре метода физических исследований: 1) опыт - наблюдение явления в четко определенные естественных условиях. 2) гипотеза - это научное предположение, описывающее явление, требующее объяснений и доказательств. 3) эксперимент - это опыт, проведенные в строго контролируемых лабораторных условиях. 4) теория - это гипотеза, подтвержденная экспериментом. Гипо́ теза — недоказанное утверждение, предположение или догадка. Как правило, гипотеза высказывается на основе ряда подтверждающих её наблюдений (примеров) и поэтому выглядит правдоподобно. Гипотезу впоследствии или доказывают, превращая её в установленный факт (см. теорема, теория), или же опровергают (например, указывая контрпример), переводя в разряд ложных утверждений.Недоказанная и неопровергнутая гипотеза называется открытой проблемой. Тео́ рия — система знаний, обладающая предсказательной силой в отношении какого-либо явления. Теории формулируются, разрабатываются и проверяются в соответствии с научным методом. Стандартный метод проверки теорий — прямая экспериментальная проверка Однако часто теорию нельзя проверить прямым экспериментом, и поэтому теории часто проверяются не прямым экспериментом, а по наличию предсказательной силы — то есть если из неё следуют неизвестные, незамеченные ранее события, и при пристальном наблюдении эти события обнаруживаются, то предсказательная сила присутствует. Экспериме́ нт в научном методе — набор действий и наблюдений, выполняемых для проверки (истинности или ложности) гипотезы или научного исследования причинных связей между феноменами. Эксперимент является краеугольным камнем эмпирического подхода к знанию. Критерий Поппера выдвигает в качестве главного отличия научной теории от псевдонаучной возможность постановки эксперимента, прежде всего такого, который может дать опровергающий эту теорию результат. Эксперимент делится на следующие этапы:
Размерность физических величин. Основные единицы СИ. Анализ размерностей. Разме́ рность физической величины — выражение, показывающее, во сколько раз изменится единица физической величины при изменении единиц величин, принятых в данной системе за основные. Размерность представляет собой одночлен, составленный из произведения обобщённых символов основных единиц в различных (целых или дробных, положительных или отрицательных) степенях, которые называются показателями размерности. Так, например, размерность скорости LT − 1, где Т представляет собой размерность времени, а L — длины. Эти символы обозначают единицы времени и длины независимо от их конкретного размера (секунда, минута, час, метр, сантиметр и т. д.).Термин размерность может относиться также к единице измерения физической величины. Часто абстрагируются от конкретных единиц измерения и описывают размерности в терминах основных физических величин, таких, например, как длина, масса и время, которые обозначают символами L, M и T, соответственно. Размерность записывают, как произведение этих символов, каждый из которых возведён в рациональнуюстепень.Например, размерность скорости — расстояние, делённое на время (LT − 1), а размерность силы — масса, умноженная на расстояние и делённая на время в квадрате (MLT − 2). В механике размерность любой величины может быть выражена через расстояние (которое физики часто называют «длиной»), массу и время. Электрические и магнитные величины также могут быть выражены через эти три размерности с использованием, например, закона Кулона. Однако, при использовании СИ иногда бывает удобнее ввести размерность такой основной физической величины, как электрический ток (I).Некоторые из физических величин безразмерны в любой системе единиц, например, постоянная тонкой структуры в квантовой физике или числа Маха, Рейнольдса, Струхаля и др. в механике сред.ВСИ определены семь единиц основных физических величин, размерности которых считаются независимыми друг от друга. Поскольку система физических величин принципиально отличается от системы единиц, то в некоторых системах физических величин возможен иной перечень основных физических величин, чем в СИ. СИ (Система Интернациональная) — международная система единиц, современный вариант метрической системы. Она определяет семь базовых единиц измерения, являющихся основой для остальных единиц СИ. Базовые единицы измерения СИ и их величины:
Названия всех единиц СИ пишутся маленькими буквами (например, метр и его символ м). У этого правила есть исключение: название единиц, названных фамилиями учёных пишутся с большой буквы(например, ампер обозначается символом А).Многие другие единицы измерения, такие как литр, формально не входят в СИ, но они «допускаются для использования совместно с СИ». Анализ размерности — метод, используемый физиками для построения обоснованных гипотез о взаимосвязи различных размерных параметров сложной физической системы. Иногда анализ размерности можно использовать для получения готовых формул. Суть метода заключается в том, что из параметров, характеризующих систему, составляется выражение, имеющее нужную размерность.При анализе размерностей формул размерность левой части уравнения должна быть равна размерности правой части уравнения. Отсутствие такого равенства говорит о неверности формулы. Однако наличие такого равенства не даёт стопроцентной гарантии верности формулы. Сложение скоростей. Относительная скорость. Сложение скоростей Скорости движения тела в различных системах отсчёта связывает между собой классический закон сложения скоростей. Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и самой подвижной системы отсчёта относительно неподвижной. 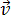 = Δ = Δ 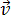 Ч + Δ Ч + Δ 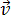 B B Это закон сложения скоростей:
Относительная скорость В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины: · абсолютное движение — это движение точки/тела в базовой СО. · относительное движение — это движение точки/тела относительно подвижной системы отсчёта. · переносное движение — это движение второй СО относительно первой. Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта: · ускорение Кориолиса. В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается. Первый закон Ньютона Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий. Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скоростью и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга. Инерциа́ льнаясисте́ ма отсчёта (ИСО ) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике: Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время —однородным. Единицы измерения массы Исторически многие меры веса были кратны эталону — массе зерна (семени) различных растений: пшеницы, ячменя, некоторых бобовых, риса, просо, горчицы, некоторых кактусов (в Америке.Грамм — изначально определялся как масса 1 см³ воды при температуре 4 °C и давлении в 1 атмосферу. В настоящее время грамм определяется как 1/1000 килограмма. Килограмм определяется как масса эталонного килограмма, хранящегося в Палате мер и весов около Парижа. Прототип килограмма изготовлен из платиноиридиевого сплава (Pt 90%, Ir 10%) в виде цилиндрической гири диаметром и высотой 39 мм. Старое определение обладало следующими недостатками: 1. Определение паскаля зависит от определения килограмма, таким образом, определение было рекурсивным. 2. Определение паскаля зависит от определения метра и секунды, таким образом, неточность в измерении длины и времени приводила к неточному измерению массы. В настоящее время § Тонна — 106 (1 000 000) граммов, или 1000 килограммов. § Центнер — 105 (100 000) граммов, или 100 килограммов. § Карат — 0, 2 грамма. Меры массы в науке § Атомная единица массы § Солнечная масса § Электронвольт Эталон единицы массы Определение единицы массы - килограмма - было дано III Генеральной конференцией по мерам и весам 1901 г. в следующем виде: " Килограмм - единица массы - представлен массой международного прототипа килограмма". При установлении метрической системы мер в качестве единицы массы была принята масса 1 кг, равная массе 1 дм3 чистой воды при температуре ее наибольшей плотности (4 °С). В этот период были проведены точные измерения массы известного объема воды путем последовательного взвешивания в воздухе и воде пустого бронзового цилиндра, размеры которого были тщательно определены.
Силы в механике Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона можно рассматривать только гравитационное и электромагнитное взаимодействия. В отличие от короткодействующих ядерного и слабого взаимодействия, гравитационное и электромагнитное взаимодействия – дальнодействующие: их действия проявляются на очень больших расстояниях.
Гравитационная сила. Две точечные массы
2. Сила тяжести. Силой тяжести тела массой
Вследствие суточного вращения Земли и несферичности ее формы величина
На высоте
Вес тела. Вес представляет собой силу, с которой тело действует на горизонтальную опору или на подвес. По величине вес и сила тяжести совпадают только в том случае, если опора неподвижна. Например, вес тела, находящегося в движущемся вверх с ускорением лифте, превышает его силу тяжести. Сила трения. При скольжении тела действующая на него сила трения
Сила упругости. Сила упругости, действующая на тело со стороны деформированной (сжатой или растянутой) пружины, равна по величине
Основная задача динамики Исторически деление на прямую и обратную задачу динамики сложилось следующим образом. § Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело. § Обратная задача динамики: по заданным силам определить характер движения тела.
Третий закон Ньютона. В §1.7 понятие массы тела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений
В векторной форме это соотношение принимает вид
Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силами
Это равенство называется третьим законом Ньютона. Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телами поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу. Рис. 1.9.1 иллюстрирует третий закон Ньютона. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.Силы, действующие между частями одного и того же тела, называются внутренними. Если тело движется как целое, то его ускорение определяется только внешней силой. Внутренние силы исключаются из второго закона Ньютона, так как их векторная сумма равна нулю. В качестве примера рассмотрим рис. 1.9.2, на котором изображены два тела с массами m1 и m2, жестко связанные между собой невесомой нерастяжимой нитью и двигающиеся с одинаковым ускорением
Складывая левые и правые части этих уравнений и принимая во внимание, что
Внутренние силы исключились из уравнения движения системы двух связанных тел. Третий закон Ньютона Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой Современная формулировка
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами. Взаимодействие тел.
Внешние и внутренние силы Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называются внешними. Внешние силы, действующие на тело, можно разделить на активные (независимые) иреактивные. Реактивные усилия возникают в связях, наложенных на тело, и определяются действующими на тело активными усилиями. По способу приложения внешние силы делятся на объемные и поверхностные. Объемные силы распределены по всему объему рассматриваемого тела и приложены к каждой его частице. В частности, к объемным силам относятся собственный вес сооружения, магнитное притяжение или силы инерции. Единицей измерения объемных сил является сила, отнесенная к единице объема кН/м3. Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рассматриваемого объекта с окружающими телами. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки подразделяются насосредоточенные и распределенные. К первым относятся нагрузки, реальная площадь приложения которых несоизмеримо меньше полной площади поверхности тела (например, воздействие колонн на фундаментную плиту достаточно больших размеров можно рассматривать как действие на нее сосредоточенных усилий). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределенная. Сосредоточенные усилия измеряются в кН, а распределенные кН/м2. Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия. Внешние силы, действующие на конструкцию, разделяют на активные силы (нагрузку) и реакции опор. По характеру действия различают сосредоточенные силы, измеряемые в ньютонах (Н, кН), распределенную нагрузку, измеряемую в ньютонах на метры (Н/м, кН/м), если нагрузка распределена вдоль линии, или в ньютонах на метр квадратный (Н/м2, кН/м2), если нагрузка распределена по поверхности, сосредоточенный момент, измеряемый в ньютонометрах (Нм, кНм) (рис. 1.2). Реакции опор вычисляют через активные силы методами теоретической механики. Под действием внешних сил стержень деформируется, при этом между отдельными частями стержня появляются дополнительные силы взаимодействия, называемые внутренними силами. Если стержень мысленно рассечь плоскостью, перпендикулярной к продольной оси стержня Z, то по всей площади поперечного сечения от одной части стержня на другую часть будут передаваться внутренние силы.Отбросим правую часть стержня. Внутренние силы, передающиеся от неё на левую часть (рис. 1.3), по отношению к левой части стержня становятся внешними силами и могут быть представлены главным вектором и главным моментом. Центром приведения принимается центр тяжести поперечного сечения стержня, через который проводят координатные оси X, Y, лежащие в плоскости сечения, и ось Z, перпендикулярную плоскости поперечного сечения. Главный вектор раскладывается на силы N, Qx, Qy, а главный момент – на моменты Mx, My, Mz. Указанные шесть величин называют внутренними усилиями (внутренними силовыми факторами) стержня. Каждое из них имеет своё название: N – продольная (нормальная) сила, Qx и Qy – поперечные (перерезывающие) силы, Мх и Мy – изгибающие моменты, Мz – крутящий момент. Закон сохранения импульса. При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона. Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через
где
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение. Зако́ н сохране́ ния и́ мпульса (Зако́ н сохране́ ния количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну изфундаментальных симметрий, — однородность пространства. Центр инерции. Теорема о движении центра инерции. Примеры. Центр инерции Импульс замкнутой механической системы имеет различные значения по отношению к различным инерциальным системам отсчета. Если система отсчета K'движется относительно системы K со скоростью V, то скорости частиц v'α и vα в этих системах связаны соотношением vα = v'α + V. Поэтому связь между значениями P и P' импульса в этих системах дается формулой:
или
Всегда можно подобрать такую систему отсчета K', в которой полный импульс обращается в нуль. Положив P' =0, находим, что скорость этой системы отсчета
Если полный импульс механической системы равен нулю, то говорят, что она покоится относительно соответствующей системы координат. Скорость V имеет смысл скорости движения механической системы как целого с отличным от нуля импульсом. Связь между импульсом P и скоростью V системы как целого такая же, какая была бы между импульсом и скоростью одной материальной точки с массой, равной сумме масс в системе, Правая сторона формулы (1.71) может быть представлена как полная производная по времени от выражения:
Можно сказать, что скорость V системы как целого есть скорость перемещения в пространстве точки, радиус-вектор которой дается формулой (1.72). Такая точка является центром инерции системы. Закон сохранения импульса замкнутой системы можно сформулировать как утверждение о том, что ее центр инерции движется прямолинейно и равномерно. Это есть обобщение закона инерции для свободной материальной точки. Энергию покоящейся как целое механической системы обычно называют ее внутренней энергией Eвн. Она состоит из кинетической энергии движения частиц относительно друг друга и потенциальной энергии их взаимодействия. Полная же энергия системы, движущейся как целое со скоростью V,
ЦЕНТР ИНЕРЦИИ (центр масс) - геом. точка, положение к-рой характеризует распределение масс в теле или механич. системе. Координаты Ц. и. определяются ф-лами
или для тела при непрерывном распределении масс
где mk - массы материальных точек, образующих систему; xk, yk, zk- координаты этих точек; М =Smk- масса системы; r( х, у, z) - плотность; V- объём. Понятие Ц. и. отличается от понятия центра тяжести тем, что последнее имеет смысл только для твёрдого тела, находящегося в однородном поле тяжести; понятие же Ц. и. не связано ни с каким силовым полем и имеет смысл для любой механич. системы. Для твёрдого тела положения Ц. и. и центра тяжести совпадают. При движении механич. системы её Ц. и. движется так, как двигалась бы материальная точка, имеющая массу, равную массе системы, и находящаяся под действием всех внеш. сил, приложенных к системе. Кроме того, нек-рыеур-ния движения механич. системы (тела) по отношению к осям, имеющим начало в Ц. и. и движущимся вместе с Ц. и. поступательно, сохраняют тот же вид, что и для движения по отношению к инерциальной системе отсчёта. Ввиду этих свойств понятие о Ц. и. играет важную роль в динамике системы и твёрдого тела. С. М. Торг. Движение тел с переменной массой. Примеры. |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 8278; Нарушение авторского права страницы