Запишем 2-й закон Ньютона для каждого тела механического тела

.
.
.
.
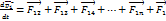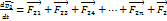Всё сложим:
.
Учитывая, что сумма .
.
.

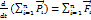- суммарный импульс механической системы.
- равнодействующая внешних сил действующих на механическую систему.
Механическая система на. Замкнутой, если равнодействующая внешних сил равна 0. Для замкнутой системы .

- импульс замкнутой системы.

Если система не замкнутая, но если проекция сил на какое-то направление будет равно «0», то будет выполняться закон сохранения импулься в этом направлении.

P_1x + P_2x + … = const.

В основе сохранения импульса лежит однородность пространств, т.е. одинаковость свойств пространства во всех его точках.
Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механических свойств системы.

 

Вопрос.
Центр масс (инерции). Теорема движения центра масс (инерции).

Центром масс (инерции) тела наз. такая точка «С» положение которой определяется выражением.

Нахождение центра масс:

;
;;
;

И< 𝑡.орость центра масс => центр масс замкнутой системы либо движется прямолинейно и равномерно, и равно 0, либо остаётсямпульс системы может быть представлен в виде: ; 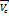- скорость центра масс.
;
Если система замкнутая, =const => - скорость центра масс => центр масс замкнутой системы либо движется прямолинейно и равномерно, и равно 0, либо остаётся неподвижно.
; ;
– теорема о движении центра масс механической системы.
Таким образом центр масс движется как мат. точка, в которой сосредоточена вся масса системы и на которую действует сила, равная равнодействующей всех внешних сил, действующих на механическую систему. .

Вопрос.
Кинетическая энергия и её связь с работой силы.
Кинетической энергией наз. механическую энергию всякого движущегося тела. Изменяют её той работой, которую могла бы совершить тело при его торможении до полной остановки.
.
Кинетическая энергия системы сил равна арифметической сумме кинетических энергий тел.
.
Если на частицу действует сила F, кинетическая энергия не остаётся постоянной, в этом случае элементарное изменение кинетической энергии равно:
;
;
Из последнег выражения следует: , тогда dE_k=0, E_k=const, .
;
- теорема об изменении кинетической энергии.

 

Вопрос.
Потенциальная энергия и её связь со скалярной функцией и работой сил.
Потенциальная энергия это энергия взаимодействия тел или частей одного и того же тела.
A= E_k2 – E_k1; A = П₂ – П₁ – Е_р2 +Е_р1 = - (Е_р2 - Е_р1); Е_р = -П.
Работа равна убыли потенциальной энергии из выражения вышеприведенного.
E_k2 – E_k1 = – Е_р2 +Е_р1; E_k1 +Е_р1 = E_k2 + Е_р2 – закон сохранения мех. энергии.
- сила направлена в сторону уменьшения потенциальной энергии.
Если имеются неконсервативные силы, тополная энергия:
Е_n = E_k + E_p; A = E_n1 – E_n1; E_p = mgh – потенциальной энергии от 0-го уровня. E_p0 = 0 => E_p = - mgh.
Найдём потенциальную энергию.
Закон Гука: F_упр = -kx
F = kx тогда работа:
; δ A = F·dx; - коэффициент упругости.

Вопрос.
Взаимодействие (столкновение) тел.
При соударении тел друг с другом они притерпевают деформацию, при этом кинетическая энергия которой обладали тела перед ударом частично или полностью переходят в потенциальную энергию упругой деформации и так называемую внутреннию энергию.
Увеличение внутренней энергии сопровождается повышением температуры.
Существует два предельных вида удара:
1) абсолютно упругий; 2) абсолютно неупругий.
Абсолютно упругим наз. такой удар, при котором мех. энергия тел непереходит в другие немеханические виды энергии. При таком ударе кинетическая энергия тел переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме отталкиваясь друг от друга, в итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию. При этом тела разлетаются в разные стороны, со скоростями, величина и направление которых определяются двумя условиями: 1) сохранением полной мех. энергии; 2) закон сохранения импульса.
Ограничимся взаимодействием центрального удара двух тел.

 

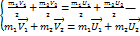-- закон сохранения импульса.

=> U₂ = V₁ + U₁ – V₂.

;
;

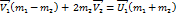m₁ = m₂; . Вывод: тела обмениваются скоростями.

Абсолютно неупругий удар – удар хар-ся тем, что потенциальная энергия деформаций не возникает, при этом кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. После удара сталкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругим ударе выполняется лишь закон сохранения импульса (закон сохранения мех. энергии не выполняется), часть мех. энергии переходит во внутрению энергию – тепло.

- работа по деформации.

Вопрос.
Динамика вращательного движения.
Момент силы (вращательный момент). Момент импульса, основной закон динамики вращательного движения.
рассмотрим закономерности движения твердого тела закрепленного в одной неподвижной точки «0», вокруг которой тело может свободно вращаться.
Запишем 2-й закон Ньютона для этой точки.
Произвольная от импульса равна этой силы.
;
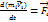Учтём: умножим векторно на :
;
;
Скалярное произведение векторов: .
Векторное произведение: .
;
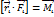- вращательный момент.
- момент импульса.
- основное уравнение динамики вращательного движения для i-той мат. точки.
;
- сумарный момент импульса для твёрдых тел.
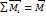- суммарный вращательный момент для твёрдых тел.
- основной закон динамики вращательного движения для всего тела.
Если рассматривать движение твёрдого тела относительно какой-то оси вращения, то:
- закон динамики вращательного движения относительно оси.

Вопрос.

⇐ Предыдущая1234Следующая ⇒

Поделиться: