
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ПОЛУЧЕНИЕ И АНАЛИЗ ПОЛЯРИЗОВАННОГО СВЕТА
Для получения поляризованного света естественное излучение какого-либо источника пропускают через поляризатор. Действие поляризатора состоит в том, что он разделяет первоначальный пучок на две компоненты со взаимно перпендикулярными направлениями поляризации, пропускает одну компоненту и поглощает или отклоняет другую. Устройства, служащие для анализа степени поляризации света, называются анализаторами. В качестве анализаторов используются те же приспособления, что и для поляризации света. СТЕПЕНЬЮ ПОЛЯРИЗАЦИИ называется величина P= СПОСОБЫ ПОЛУЧЕНИЯ ИСКУССТВЕННОЙ ОПТИЧЕСКОЙ АНИЗОТРОПИИ Оптически изотропные вещества становятся оптически анизотропными под действием: 1) одностороннего сжатия или растяжения (кристаллы кубической системы, стекла и др.); 2) электрического поля (эффект Керра, жидкости, аморфные тела, газы); 3) магнитного поля (жидкости, стекла, коллоиды). В перечисленных случаях вещество приобретает свойства одноосного кристалла, оптическая ось которого совпадает с направлением деформации, электрического или магнитного полей. ЭФФЕКТ КЕРРА — оптическая анизотропия веществ под действием электрического поля — объясняется различной поляризуемостью молекул жидкости по разным направлениям. Это явление практически безынерционно, т. е. время перехода вещества из изотропного состояния в анизотропное при включении поля (и обратно) составляет приблизительно Естественной оптической активностью называется способность среды вызывать вращение плоскости поляризации проходящего через нее линейно поляризованного света. Такие среды получили название оптически активных. Искусственная (наведенная) оптическая активность возникает в магнитном поле (эффект Фарадея). Знак вращения в эффекте Фарадея зависит как от магнитных свойств среды, так и от того, вдоль поля или против него распространяется излучение. Это связано с особым характером магнитного поля. Если линейно-поляризованный свет, прошедший через слой вещества с естественной оптической активностью, отражается и проходит через тот же слой в обратном направлении, восстанавливается исходная поляризация, тогда как в среде с наведённой оптической активностью в аналогичном опыте угол поворота удвоится. ДИСПЕРСИЕЙ СВЕТА называют зависимость показателя преломления n от длины волны (или от частоты). Дисперсия света при преломлении обусловлена зависимостью показателя преломления n среды от частоты w света; в прозрачном веществе наблюдается увеличение n с ростом w ( нормальная дисперсия ), возможно и уменьшение n с увеличением w ( аномальная дисперсия ). ЭЛЕКТРОННАЯ ТЕОРИЯ ДИСПЕРСИИ СВЕТА В электронной теории дисперсия рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны. Диэлектрическая проницаемость, по определению, равна:
ВЫВОД ЗАКОНА ПРЕЛОМЛЕНИЯ НА ОСНОВЕ ПРИНЦЕПА ГЮГЕНСА
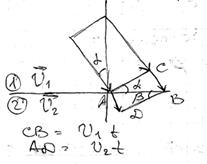
|
Последнее изменение этой страницы: 2017-03-14; Просмотров: 628; Нарушение авторского права страницы