Дифференциальное уравнение затухающих механических и электромагнитных колебаний и его решение. Апериодический процесс.

ифференциальное уравнение свободных затухающих колебаний линейной системы определяется как
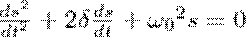(1)
где s – колеблющаяся величина, которая описывает тот или иной физический процесс, δ = const — коэффициент затухания, ω 0 - циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.
Решение уравнения (1) запишем в виде
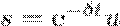(2) где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем 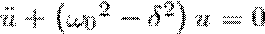(3)
Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положителньного коэффициента: 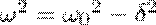(4)
(если (ω 02 - σ 2)> 0, то такое обозначение мы вправе сделать). Тогда получим выражение 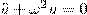, у которого решение будет функция 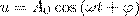. Значит, решение уравнения (1) в случае малых затуханий (ω 02 > > σ 2 )

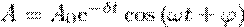(5) где 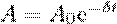(6) — амплитуда затухающих колебаний, а А0 — начальная амплитуда. Выражение (5) представлено графики рис. 1 сплошной линией, а (6) — штриховыми линиями. Промежуток времени τ = 1/σ, в течение которого амплитуда затухающих колебаний становится мешьше в е раз, называется временем релаксации.

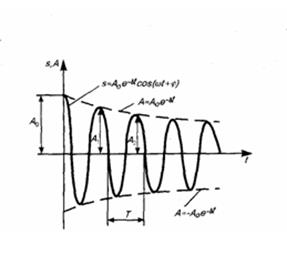Затухание не дает колебаниям быть периодичными и, строго говоря, к ним нельзя применять понятие периода или частоты. Но если затухание мало, то можно условно использовать понятие периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис. 1). В этом случае период затухающих колебаний с учетом выражения (4) будет равен

Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, которые отличаются на период, то отношение
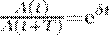называется декрементом затухания, а его логарифм

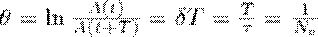(7)
— логарифмическим декрементом затухания; Ne — число колебаний, которые совершаются за время уменьшения амплитуды в е раз. Логарифмический декремент затухания является постоянной величиной для данной колебательной системы.
Для характеристики колебательной системы также применяют понятие добротности Q, которая при малых значениях логарифмического декремента будет равна
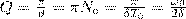(8)
(так как затухание мало (ω 02 > > σ 2 ), то T принято равным Т0).
Из формулы (8) вытекает, что добротность пропорциональна числу колебаний Ne, которые система совершает за время релаксации.
Выводы и уравнения, полученные для свободных затухающих колебаний линейных систем, можно использовать для колебаний различной физической природы — механических (в качестве примера возьмем пружинный маятник) и электромагнитных (в качестве примера возьмем электрический колебательный контур).
1. Свободные затухающие колебания пружинного маятника. Для пружинного маятника массой m, который совершает малые колебания под действием упругой силы F= -kx, сила трения прямо пропорциональна скорости, т. е.
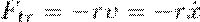где r — коэффициент сопротивления; знак минус говорит о том, что сила трения и скорость противоположно направлены.
При этих условиях закон движения маятника 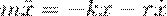(9) Используя формулу 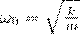и считая, что коэффициент затухания равен 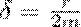(10) получим полностью идентичное уравнению (1) дифференциальное уравнение затухающих колебаний маятника:

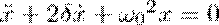
Из выражений (1) и (5) следует, что колебания маятника удовлетворяют уравнению

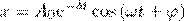
где частота 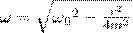(см. (4)).
Добротность пружинного маятника, используя (8) и (10), .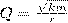

2. Свободные затухающие колебания в электрическом колебательном контуре. Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R≠ 0), как известно

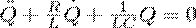
Учитывая формулу собственной частоты колебательного контура и принимая коэффициент затухания равным
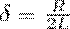(11)
дифференциальное уравнение колебаний заряда Q (см. раздел " Свободные гармонические колебания в колебательном контуре" ) можно записать в аналогичном уравнению (1) виде

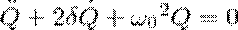
Из зависимостей (1) и (5) следует, что колебания заряда подчиняются закону
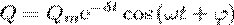(12)
с частотой, используя (4), равной
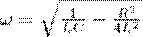(13)
меньшей собственной частоты контура ω 0. При R=0 формула (13) становится формулой Логарифмческий декремент затухания задается формулой (7), а добротность колебательного контура (8)
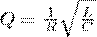(14)
Отметим в заключение, что при увеличении коэффициента затухания δ период затухающих колебании увеличивается и при δ =ω 0равен бесконечности, т. е. движение перестает быть периодическим. В этом случае колеблющаяся величина асимптотически стремится к нулю, когда t→ ∞. Данный процесс не будет колебательным. Он называется апериодическим.

⇐ Предыдущая123456Следующая ⇒

Поделиться: