
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Натуральный триэдр траектории.Стр 1 из 6Следующая ⇒
КИНЕМАТИКА __________________________________________________________ В разделе кинематики мы изучаем движение и устанавливаем основные пространственно – временные характеристики движения. В настоящем разделе, посвященном кинематике, отвлекаются от силовых взаимодействий между материальными телами и влияния на них силовых полей, а рассматривают механические движения тел, в отрыве от причин, которые создают и поддерживают эти движения. Движения в кинематике изучаются по отношению к некоторой системе отсчёта, представляющей жесткую, неограниченно простирающуюся во все стороны систему точек. В кинематике неважно, движется ли эта система или принимается неподвижной. Отметим, что такое равноправие систем не имеет места в динамике. В этом пространстве выбирается тело отсчёта, а в нём систему координат, например, три взаимно перпендикулярные координатные оси, служащие для определения положения отдельных точек тел. Как указывалось в начале, пространство рассматривается как евклидово, так, применение теоремы Пифагора позволяет определить квадрат расстояния между двумя точками как сумму квадратов разностей соответствующих координат точек и т. п. Наряду с абсолютным пространством в классической кинематике используется понятие «абсолютного времени», одинаково и равномерно текущего во всех точках абсолютного пространства. В качестве такого времени принимается звёздное или среднее солнечное время. Заметим, что все выводы классической механики с достаточной для практики точностью справедливы, если скорости движения малы по сравнению со скоростью распространения света, а размеры областей пространства, в которых происходит движение, далеки от космических расстояний.
Глава 4.
Кинематика точки. § 1. Способы задания движения точки. Уравнения движения точки; траектория. 1. Координатный способ задания положения и движения точки. Положение точки в пространстве (рис. 17) будем определять ее вектор-радиусом
х= ρ соsφ = r sin θ cos φ = r cos ψ соsφ, у =ρ sin φ = r sin θ sin φ = r cos ψ sin φ, (2.1) z = r cos θ = r sin ψ. Если точка движется в пространстве, то ее координаты изменяются с течением времени. По закону изменения этих координат можно судить о характере движения точки. Предположим, что нам заданы координаты точки в функции времени, т. е. заданы уравнения
Эти уравнения называются уравнениями движения точки в декартовых координатах. Вместо декартовых координат х, у, z можно взять какие угодно другие координаты: полярные, сферические, цилиндрические и др. Выраженные в функции времени, они дадут уравнения движения точки в соответствующей системе координат. 2. Естественный способ задания точки.
Скорость точки. Пусть за время
Вектор скорости точки равен векторной производной вектор-радиуса точки по времени и направлен по касательной к траектории движения точки. Разложим вектор-радиус
Дифференцируя обе части этого равенства по времени и учитывая, что орты постоянны по величине и направлению будем иметь
что позволяет записать
Модуль скорости равен
Ускорение точки. В общем случае движение точки происходит с переменной по величине и по направлению скоростью. Желая охарактеризовать изменение скорости, вводят меру быстроты этого изменения со временем — ускорение, которое должно учитывать векторное (геометрическое) изменение скорости, т. е. изменение ее по величине и по направлению. Для этого рассмотрим (как и для скорости) два значения скорости в моменты времени
Если радиус – вектор представлен разложением по ортам декартовой системы координат
и
Модуль ускорения равен
Считая
но
Равенство (2.7) представляет собой разложение вектора ускорения по осям натурального триэдра. Обозначив коэффициенты при единичных векторах,
причем из (2.7) следует, что
Последнее равенство говорит о том, что вектор ускорения перпендикулярен к бинормали, т. е. ускорение лежит в соприкасающейся плоскости. Первое слагаемое в разложении (2.7) - Итак, вектор ускорения в криволинейном движении может быть представлен как геометрическая сумма двух ускорений: касательного и нормального. Величина ускорения может быть представлена так:
Рассмотрим два частных случая: а) Случай равномерного движения; величина скорости постоянна, так что б) Случай прямолинейного движения; кривизна прямой линии равна нулю и, следовательно, Из сопоставления этих двух случаев следует, что в равномерном прямолинейном движении ускорение равно нулю. Отметим, что не следует смешивать Твердого тела.
Так как
Эта основная формула кинематики твердого тела дает закон распределения скоростей в твердом теле в общем случае его движения. Слагаемое Зная движение полюса и закон вращения тела вокруг полюса, т. е. имея уравнения движения, можем по формуле (2.30) определить скорость любой точки тела. Проекции скорости на оси получим по общим правилам проектирования векторных выражений. Выпишем проекции скорости на неподвижные оси:
Здесь
или
Первое слагаемое
Глава 8.
Вопросы для самопроверки по кинематике. 1. Векторная формула скорости точки. Чему равна скорость точки, если ее движение задано законом
2. Векторная формула ускорения точки. Чему равно ускорение точки, если ее движение задано законом x(t)= y(t)= 3. Формула нормального ускорения точки. Когда оно равно нулю? 4. Чему равно касательное ускорение точки, если ее движение задано законом 5. Как направлен вектор угловой скорости и вектор углового ускорения тела, вращающегося вокруг неподвижной оси? 6. Какие ускорения точек тела, вращающегося вокруг неподвижной оси Вам известны? 7. Чему равно и как направлено осестремительное ускорение (скалярная и векторная форма записи)? 8. 9. Определите скорости и угловую скорость плоской фигуры, представленной на рис., если известны 10.
11. 12. Определить угловую скорость и угловое ускорение стержня, если АВ=l. 13. Какие углы определяют положение тела, вращающегося вокруг неподвижной точки? 14. Векторная формула скорости точек тела, вращающегося вокруг неподвижной точки. 15. Как определяется угловое ускорение тела, вращающегося вокруг неподвижной точки, прокомментируйте введенные обозначения. 16. Векторная формула сложения скоростей, чему равна переносная скорость точки? 17. 18. Чему равно абсолютное ускорение точки в указанном примере? Кольцо радиуса R вращается вокруг неподвижной оси с постоянной угловой скоростью ω.. По кольцу движется точка с постоянной скоростью u. Определить абсолютное ускорение точки, когда она находится в верхнем положении. 19. 20. Чему равно и как направлено ускорение Кориолиса точки, двигающейся со скоростью 2 м/с по шатуну АВ, когда кривошип ОА вращается с угловой скоростью 1рад/с. Угол наклона кривошипа с горизонтальной плоскостью равен π /3, АВ=3 АО? 21. Угловая скорость вращения тела относительно параллельных осей. Что такое мгновенно поступательное движение? 48. Напишите формулу Виллиса.
КИНЕМАТИКА __________________________________________________________ В разделе кинематики мы изучаем движение и устанавливаем основные пространственно – временные характеристики движения. В настоящем разделе, посвященном кинематике, отвлекаются от силовых взаимодействий между материальными телами и влияния на них силовых полей, а рассматривают механические движения тел, в отрыве от причин, которые создают и поддерживают эти движения. Движения в кинематике изучаются по отношению к некоторой системе отсчёта, представляющей жесткую, неограниченно простирающуюся во все стороны систему точек. В кинематике неважно, движется ли эта система или принимается неподвижной. Отметим, что такое равноправие систем не имеет места в динамике. В этом пространстве выбирается тело отсчёта, а в нём систему координат, например, три взаимно перпендикулярные координатные оси, служащие для определения положения отдельных точек тел. Как указывалось в начале, пространство рассматривается как евклидово, так, применение теоремы Пифагора позволяет определить квадрат расстояния между двумя точками как сумму квадратов разностей соответствующих координат точек и т. п. Наряду с абсолютным пространством в классической кинематике используется понятие «абсолютного времени», одинаково и равномерно текущего во всех точках абсолютного пространства. В качестве такого времени принимается звёздное или среднее солнечное время. Заметим, что все выводы классической механики с достаточной для практики точностью справедливы, если скорости движения малы по сравнению со скоростью распространения света, а размеры областей пространства, в которых происходит движение, далеки от космических расстояний.
Глава 4.
Кинематика точки. § 1. Способы задания движения точки. Уравнения движения точки; траектория. 1. Координатный способ задания положения и движения точки. Положение точки в пространстве (рис. 17) будем определять ее вектор-радиусом
х= ρ соsφ = r sin θ cos φ = r cos ψ соsφ, у =ρ sin φ = r sin θ sin φ = r cos ψ sin φ, (2.1) z = r cos θ = r sin ψ. Если точка движется в пространстве, то ее координаты изменяются с течением времени. По закону изменения этих координат можно судить о характере движения точки. Предположим, что нам заданы координаты точки в функции времени, т. е. заданы уравнения
Эти уравнения называются уравнениями движения точки в декартовых координатах. Вместо декартовых координат х, у, z можно взять какие угодно другие координаты: полярные, сферические, цилиндрические и др. Выраженные в функции времени, они дадут уравнения движения точки в соответствующей системе координат. 2. Естественный способ задания точки.
Натуральный триэдр траектории.
Величину или модуль производной будем обозначать через
При дифференцировании векторов сохраняются те же правила, что и при дифференцировании функций: производная геометрической суммы (разности) вектор–функции равна геометрической сумме (разности) производных. Точно так же сохраняется и правило дифференцирования произведения скалярной функции X (u) на вектор
Понятие вектор – функции и её производной облегчают рассмотрение основных геометрических свойств траектории, необходимых для развития представления о скорости и ускорения точки. Рассмотрим некоторую кривую, лежащую (вообще говоря) не в одной плоскости. Возьмём на этой кривой три точки М1, М2 и М. Проведём через эти три точки плоскость (предполагается, что три точки не лежат на одной прямой). Устремим точки М1 и М2 к точке М. Проведённая плоскость при этом будет каким – то образом поворачиваться и займёт предельное положения, когда все три точки сольются. Это предельное положение назовём соприкасающейся плоскостью (СП), в которой проведём касательную к кривой в точке М. Орт касательной в точке М обозначим Совокупность трех взаимно перпендикулярных осей: 1) касательной, направленной в сторону возрастания дуги, 2) главной нормали, направленной в сторону вогнутости кривой, и 3) бинормали, перпендикулярной к касательной и главной нормали образует так называемый натуральней триэдр кривой. Единичные векторы этих осей обозначим соответственно через
 . Если точка М1 взята на весьма малом расстоянии Δ S от точки М, то угол α (угол смежности) будет также мал и вектор . Если точка М1 взята на весьма малом расстоянии Δ S от точки М, то угол α (угол смежности) будет также мал и вектор  , с тем меньшей ошибкой, чем меньше Δ S, можно считать перпендикулярным к , с тем меньшей ошибкой, чем меньше Δ S, можно считать перпендикулярным к  и, следовательно, параллельным вектору нормали и, следовательно, параллельным вектору нормали  , лежащему с , лежащему с  в одной и той же плоскости. По абсолютной величине в одной и той же плоскости. По абсолютной величине  (как основание равнобедренного треугольника с малым углом α при вершине и боковыми сторонами, равными единице) будет равен (как основание равнобедренного треугольника с малым углом α при вершине и боковыми сторонами, равными единице) будет равен  Отсюда найдем (с точностью до малых высших порядков): Отсюда найдем (с точностью до малых высших порядков):  или или  . Будем приближать Δ S к нулю, тогда точка M1 будет стремиться к М, единичный вектор нормали . Будем приближать Δ S к нулю, тогда точка M1 будет стремиться к М, единичный вектор нормали  — к искомому единичному вектору — к искомому единичному вектору 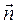 , и мы будем иметь: , и мы будем иметь:  . Второй множитель определяет кривизну кривой в данной точке, величина обратная кривизне – ρ называется радиусом кривизны . Второй множитель определяет кривизну кривой в данной точке, величина обратная кривизне – ρ называется радиусом кривизны
Таким образом, имеем следующее выражение орта главной нормали
Скорость точки. Пусть за время
Вектор скорости точки равен векторной производной вектор-радиуса точки по времени и направлен по касательной к траектории движения точки. Разложим вектор-радиус
Дифференцируя обе части этого равенства по времени и учитывая, что орты постоянны по величине и направлению будем иметь
что позволяет записать
Модуль скорости равен
Ускорение точки. В общем случае движение точки происходит с переменной по величине и по направлению скоростью. Желая охарактеризовать изменение скорости, вводят меру быстроты этого изменения со временем — ускорение, которое должно учитывать векторное (геометрическое) изменение скорости, т. е. изменение ее по величине и по направлению. Для этого рассмотрим (как и для скорости) два значения скорости в моменты времени
Если радиус – вектор представлен разложением по ортам декартовой системы координат
и
Модуль ускорения равен
Считая
но
Равенство (2.7) представляет собой разложение вектора ускорения по осям натурального триэдра. Обозначив коэффициенты при единичных векторах,
причем из (2.7) следует, что
Последнее равенство говорит о том, что вектор ускорения перпендикулярен к бинормали, т. е. ускорение лежит в соприкасающейся плоскости. Первое слагаемое в разложении (2.7) - Итак, вектор ускорения в криволинейном движении может быть представлен как геометрическая сумма двух ускорений: касательного и нормального. Величина ускорения может быть представлена так:
Рассмотрим два частных случая: а) Случай равномерного движения; величина скорости постоянна, так что б) Случай прямолинейного движения; кривизна прямой линии равна нулю и, следовательно, Из сопоставления этих двух случаев следует, что в равномерном прямолинейном движении ускорение равно нулю. Отметим, что не следует смешивать |
Последнее изменение этой страницы: 2017-03-15; Просмотров: 1191; Нарушение авторского права страницы