МАТЕМАТКА 2 (Спецглавы математики)

Е.Ю. Романова

 

МАТЕМАТКА 2 (Спецглавы математики)

 

Методические рекомендации по самостоятельному изучению дисциплины

для студентов инженерного факультета

специальности 23.05.01

 

Тверь

Тверская ГСХА

 

Романова Е.Ю. Математика 2 (Спецглавы математики): методические рекомендации по самостоятельному изучению дисциплины для студентов инженерного факультета специальности 23.05.01/ Е.Ю. Романова. – Тверь: Тверская ГСХА, 2016. – 82 с.

 

Методические рекомендации рассмотрены и утверждены на заседании предметно-методической комиссии кафедры ФМД и ИТ (протокол № 1 от 12 сентября 2016 г.).

 

 

Методические рекомендации по самостоятельному изучению дисциплины «Математика» содержит тематику и задания для самостоятельной подготовки к занятиям, способствуют усвоению и закреплению пройденного материала и проверке знаний.

 

Методические указания предназначены для студентов инженерного факультета специальности 23.05.01.

 

Самостоятельная работа студентов по дисциплине «Математика» предполагает изучение теоретического и практического материала по актуальным вопросам дисциплины. Рекомендуется самостоятельное изучение учебной и научной литературы. Самостоятельно изученные теоретические материалы предоставляются в виде рефератов или докладов, которые обсуждаются на практических занятиях. Информационными источниками могут выступать периодические издания, материалы интернет - ресурсов и т.д. Оформление работы должно соответствовать общепринятым требованиям и стандартам.

При выдаче заданий на самостоятельную работу используется дифференцированный подход к студентам. Перед выполнением студентами самостоятельной внеаудиторной работы преподаватель проводит инструктаж по выполнению задания, который включает: цель задания, его содержание, сроки выполнения, ориентировочный объем работы, основные требования к результатам работы, критерии оценки. В процессе инструктажа студенты предупреждаются о возможных типичных ошибках, встречающихся при выполнении задания.

Самостоятельная работа осуществляется индивидуально. Контроль самостоятельной работы организуется в двух формах:

· самоконтроль и самооценка студента (тесты самопроверки);

· контроль со стороны преподавателей (текущий и промежуточный).

Текущий контроль осуществляется на практических занятиях, промежуточный контроль осуществляется на экзамене в устной форме.

Критериями оценки результатов самостоятельной работы студента являются:

· уровень освоения студентом учебного материала;

· умение студента использовать теоретические знания при выполнении практических задач;

· обоснованность и четкость изложения ответа;

· оформление материала в соответствии с требованиями.

Решение.

а) Плотность вероятности

б) Р (x = 1) = 0 как вероятность отдельно взятого значения непрерывной случайной величины.

P (x < 1) можно найти по определению функции распределения F (x):

P (x < 1) = F (1) = = .

P (1≤ x≤ 2) можно найти как приращение функции распре­де­ления по свойству 4⁰ функции F (x):

P (1≤ x ≤ 2) = f (2) – F (1) = = .

в) Математическое ожидание находим по формуле

.

 

Дисперсию найдем, учитывая формулу

.

Вначале найдем

.

Теперь .

 

Пример 13. Дана функция

При каком значении параметра С эта функция является плотностью распределения некоторой непрерывной случайной величины x? Для нее найти: а) функцию распределения F (х); б) Р ( x | ≤ 2).

Решение. Данная функция может являться плотностью распределения некоторой случайной величины, если

.

Из этого условия найдем константу С. Имеем:

.

Отсюда .

Вычислим

.

Следовательно, С = 1.

а) функция распределения

.

при х ≤ 0:

.

При x > 0:

.

Следовательно,

89 90

б) P (| x | ≤ 2) = P (– 2≤ x≤ 2) = F (2) – F (–2 ) = 1 – e^{– 2}(2+1)– – 0 = .

 

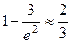Основные законы распределения

Пример 14. Торговый агент связывается с пятью потенциальными покупателями, предлагая им товар своей фирмы. Опыт показывает, что вероятность заключения сделки - 0, 15. Составить закон распределения случайной величины – количество сделок, которые удается заключить этому агенту, найти математическое ожидание и дисперсию этой случайной величины.

Решение. Случайная величина x – число сделок, которые удается заключить агенту, имеет биноминальный закон распределения с параметрами n = 5, p = 0, 15. Закон распределения x имеет вид:

x: .

Значения р_к = P (x = k), (k = 0, 1, 2, 3, 4, 5) вычислены по формуле Бернулли (11):

.

Найдем математическое ожидание и дисперсию величины x по формулам (15)

M [ x ] = np = 5 · 0, 15 = 0, 75,

D [ x ] = npq = 5· 0, 15 · 0, 85 = 0, 6375.

 

Пример 15. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за пять минут поступит: а) два вызова; б) менее двух вызовов; в) не менее двух вызовов.

Решение. Случайная величина x – число вызовов, поступающих на АТС за пять минут, имеет пуассоновское распределение с параметром а = lt, где l – среднее число вызовов, поступающих на АТС за одну минуту, t = 5, следовательно, а = 2 · 5 = 10.

Тогда по формуле Пуассона

, k = 0, 1, 2, …, имеем:

а) ;

б)

в) .

При вычислении использована таблица III приложения.

 

Пример 16. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты. Найти математическое ожидание и среднее квадратическое отклонение случайной величины x – времени ожидания поезда.

Решение. Случайная величина x – время ожидания поезда на временном (в минутах) отрезке [0, 2] имеет равномерный закон распределения, плотность вероятности которой равна:

Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна:

.

По формулам (9) находим

M [ x ] мин., D [ x ] ,

мин.

 

Пример 17. Установлено, что время ремонта телевизоров есть случайная величина x, распределенная по показательному закону. Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины x.

Решение. по условию математическое ожидание , откуда параметр l = . Следовательно, плотность вероятности

; (х ≥ 0).

Искомую вероятность найдем, используя функцию распределения:

.

Среднее квадратическое отклонение равно

дней.

 

Пример 18. Длительность времени безотказной работы элемента имеет показательное распределение F (t) = 1 – e ^{–0, 01t} (t > 0). Найти вероятность того, что за время длительностью t = 50 ч.: а) элемент откажет; б) элемент не откажет.

Решение. Обозначим через Т непрерывную случайную величину – длительность времени безотказной работы элемента. Тогда функция распределения

F (t ) = P (T < t)

определяет вероятность отказа элемента за время t, тогда вероятность безотказной работы элемента за время t, то есть

P (T > t) = 1 – F (t).

Отсюда получаем:

а) P (T < 50) = F (50) = = = 1 – 0, 606 = 0, 394;

б) P (T > 50) = 1 – F (50) = = 0, 606.

 

Пример 19. Длина изготавливаемой автоматом детали представляет собой случайную величину x, распределенную по нормальному закону с параметрами m_x = a = 15см., см.

а) найти вероятность брака, если допускаемые размеры детали должны быть 15 ± 0, 3 (см).

б) какую точность длины можно гарантировать с вероятностью 0, 97?

Решение. Так как , то

Тогда вероятность брака

б) Имеем , а = 15, e –?

с другой стороны,

.

Следовательно,

.

По таблице II приложения находим

; e = 2, 17 · = 2, 17 · 0, 2 = 0, 434 (см).

Следовательно, с вероятностью 0, 97 можно гарантировать размеры 15 ± 0, 434 (см).

Совместный закон распределения двух случайных величин

 

Пример 20. В двух урнах содержатся шары, по 6 шаров в каждой. В первой урне один шар с №1, два шара с №2, три шара с №3; во второй урне два шара с №1, три шара с №2 и один шар с номером №3. Рассматриваются случайные величины:

x₁ – номер шара, извлеченного из первой урны,

x₂ – номер шара, извлеченного из второй урны.

Из каждой урны извлекли по шару. Найти закон распределения случайной точки (x₁, x₂) и ее числовые характеристики.

решение. Закон распределения случайной точки (x₁, x₂) имеет вид:

 

x2 x1					Вероятности pij вычисля­ются следующим образом: p11 = P (x1 =1 и x2 = 1) = = Р(x1 =1) · Р(x2 = 1) = = = . p22 = P (x1 =2 и x2 = 2) = = Р(x1 =2) · Р(x2 = 2) = = = .

По закону распределения случайной точки (x₁, x₂) можно составить законы распределения случайных величин x₁ и x₂.

x₁ : , x₂ : .

;

.

Имеем:

x₁ : , x₂ : .

;

;

;

;

.

; .

Коэффициент корреляции найдем по формуле

.

Имеем

.

Тогда .

Этот результат можно предвидеть, так как x₁ и x₂ независимы из условия.

 

Пример 21. Ниже приведены данные о заработной плате работников определенной отрасли. Было обследовано 100 человек.

 

Зарплата в долларах	190-192	192-194	194-196	196-198	198-200	200-202	202-204	204-206	206-208
Число человек (ni)

 

Пусть случайная величина ξ – зарплата наугад взятого работника. Требуется для случайной величины ξ:

1. Составить выборочное распределение.

2. Построить гистограмму и график выборочной функции распределения.

3. Найти состоятельные и несмещенные оценки математического ожидания и дисперсии.

4. Построить доверительные интервалы для математического ожидания и дисперсии с уровнем доверия р = 0, 95.

5. На основании анализа формы полученной гистограммы выдвинуть гипотезу о законе распределения и проверить справедливость гипотезы по критерию Пирсона с уровнем значимости α = 0, 05.

Решение:

1. Составим таблицу, учитывая, что объем выборки n = 100, получим:

190-192	192-194	194-196	196-198	198-200	200-202	202-204	204-206	206-208

 

 

2. Построим гистограмму:

Для построения графика выборочной функции распределения составим следующую таблицу:

 

191								207

 

3. Найдем оценки математического ожидания а^* и дисперсии D^*.

Если в качестве элементов выборки взять середины интервалов β _i, i = 1, 2, …, m, тогда:

где n_i – частоты попадания в интервал (даны в условии).

Тогда получим:

4. Построим доверительные интервалы для математического ожидания и дисперсии.

С р = 0, 95 имеют место интервальные оценки:

По таблице квантилей (IV, V) найдем:

t_{0, 975}(99)=1, 99;

Подставляя эти значения, получим:

с вероятностью 0, 95 верны неравенства

5. Построенная гистограмма по форме напоминает график плотности вероятности нормального распределения. Поэтому естественно выдвинуть гипотезу о нормальном распределении случайной величины ξ. Проверим справедливость выдвинутой гипотезы по критерию Пирсона с уровнем значимости α = 0, 05. Тогда гипотетическая функция распределения случайной величины ξ имеет вид:

.

Далее используем правило проверки гипотезы.

1. Вычисляем квантиль

Имеем р = 1-α = 0, 95, m = 9, l = 2.

По таблице IV приложения находим

2. Вычисляем Z_выб. Для этого удобно результаты вычислений вносить в следующую таблицу

 

Рк	0, 002	0, 0512	0, 1158	0, 2099	0, 2548	0, 2058	0, 1106	0, 0395	0, 0094

 

Вероятности попадания р_i в интервалы будем вычислять по формуле

Было получено а^*=198, 96, σ ^*=3, 07.

 

3. Окончательно имеем

Z_выб=4, 151< 12, 6=

что означает: гипотезу о нормальном распределении случайной величины ξ принимаем.

 

II. Задачи для самостоятельного решения

Случайные величины

5.1. В связке 5 ключей, из которых один открывает дверь. Найти закон распределения и числовые характеристики случайной величины x – числа попыток открыть дверь.

5.2. Линия связи состоит из 4-х участков. На одной из них произошел обрыв связи. Вероятность обрыва на каждом участке одинакова. Найти закон распределения числа проверенных участков.

5.3. У стрелка 4 патрона. Вероятность попадания при одном выстреле равна . Стрельба ведется до первого попадания или до израсходования всех патронов. составить закон распределения случайной величины – числа израсходованных патронов.

5.4. игральная кость бросается три раза. Найти закон распределения числа выпадений шестерки.

5.5. Вероятность успеха при одном испытании равна . найти закон распределения и числовые характеристики числа успехов после 4-х независимых испытаний.

5.6. Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания в нее первым стрелком равна 0, 5; вторым – 0, 4. Составить закон распределения числа попаданий при двух выстрелах. Найти математическое ожидание и дисперсию числа попаданий. Построить график функции распределения.

5.7. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения случайной величины x – числа стандартных деталей среди отобранных. Найти числовые характеристики этой случайной величины.

5.8.

103 104

Мастер делает попытки обнаружить неисправность и при этом до конца смены успевает сделать не более трех попыток. Вероятность обнаружения неисправности при одной попытке равна 0, 6. составить закон распределения числа производимых попыток.

5.9. В лотерее из 100 билетов разыгрываются два выигрыша на сумму 200 руб. и 60 руб. Стоимость билета 10 руб. Составить закон распределения суммы чистого выигрыша для лица, купившего 2 билета.

5.10. Студент знает 10 из 15 экзаменационных вопросов. Ему задают два вопроса, случайным образом выбранные из списка. Случайная величина Х – число вопросов, на которые ответил студент. Найти закон распределения данной случайно величины, М [Х], D [X].

5.11. Случайные величины x и h заданы законом распределе­ния:

x: , h:

Составить закон распределения суммы этих случайных величин и проверить свойство математического ожидания для суммы двух случайных величин.

5.12. Плотность вероятности случайной величины x имеет вид:

Найти: а) константу с; б) Р(x Î [– 2; 0]); в)М [x ]; г) D[x ]; д) функцию распределения F (x).

5.13. Плотность вероятности случайной величины x имеет вид:

Найти: а) константу с; б) М[x]; в) D[x];

г) P (2 < x < 10); д) функцию распределения F (x).

5.14. Плотность вероятности случайной величины x имеет вид:

Найти: а) константу с; б) P (|x|≤ 2); в) функцию распре­деления F (x).

5.15. График плотности вероятности случайной величины x имеет вид:

1) 2)

 

Найти: а) константу с; б) М [x ]; в) ; г) Р(| x | 0, 5).

5.16. График плотности вероятности случайной величины x имеет вид:

 

 

Найти: а) константу с; б) М [x ]; в) .

 

5.17. График плотности вероятности случайной величины x имеет вид:

 

Найти: а) константу с; б) М [x ]; в) .

 

 

5.18. График плотности вероятности случайной величины x имеет вид:

1) 2)

 

Найти: а) константу с; б) М [x ]; в) .

5.19. Функция распределения случайной величины x имеет вид:

1)

2)

Найти: а) Р ( 0, 5 ≤ x≤ 2, 5); б) М [ x ]; в) D [ x ].

5.20. Функция распределения случайной величины x имеет вид:

Найти: а) плотность распределения f (x); б) Р (1≤ x< 2, 5); в) m_x, .

III. Задания для контрольной работы

 

Случайные величины

5.1. В коробке 20 одинаковых катушек ниток, из них – 4 катушки с белыми нитками. Наудачу вынимают 2 катушки. Найти закон распределения и числовые характеристики числа катушек с белыми нитками среди вынутых.

5.2. Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске равна 0, 7. Найти закон распределения и числовые характеристики числа попаданий мяча в корзину.

5.3. Устройство состоит их трех независимо работающих элементов. Вероятность отказа каждого элемента 0, 1. Найти закон распределения и числовые характеристики числа отказавших элементов.

5.4. Вероятность сбоя в работе АТС равна 0, 1. Найти закон распределения и числовые характеристики числа сбоев, если в данный момент поступило 3 вызова.

5.5. Вероятность того, что при составлении бухгалтерского баланса допущена ошибка, равна 0, 3. Аудитору на заключение представлены 3 баланса предприятия. Найти закон распределения и числовые характеристики числа положительных заключений на проверяемые балансы.

5.6. Среди 10 лотерейных билетов имеется 4 выигрышных. Наудачу покупают 2 билета. Найти закон распределения и числовые характеристики числа выигрышных билетов среди купленных.

5.7. Вероятность брака при изготовлении детали данного вида 2%. Найти закон распределения и числовые характеристики числа бракованных деталей из трех наугад взятых.

5.8. Вероятность успеха при одном испытании равна 0, 8. Найти закон распределения и числовые характеристики числа успехов в серии из трех независимых испытаний.

5.9. Считая равновероятным рождение мальчика и девочки, найти закон распределения и числовые характеристики числа мальчиков в семье, имеющей 3 детей.

5.10. В городе 3 коммерческих банка. У каждого риск банкротства в течение года составляет 10%. Найти закон распределения и числовые характеристики числа банков, которые могут обанкротиться в течение следующего года.

 

Законы распределения

6.1. Случайная величина x распределена равномерно на отрезке [1, 6]. Найти функцию распределения, математическое ожидание, дисперсию.

6.2. Автобусы подходят к остановке с интервалом в 5 минут. Считая, что случайная величина x – время ожидания автобуса – распределена равномерно, найти среднее время ожидания и среднее квадратичное отклонение случайной величины.

6.3. Паром для перевозки автомашин через залив подходит к причалу через каждые два часа. Считая, что время прибытия автомашин – случайная величина x – распределена равномерно, определить среднее время ожидания автомашиной прихода парома и дисперсию времени ожидания.

6.4. Известно, что средний расход удобрений на один гектар пашни составляет 80 кг, а среднее квадратичное отклонение расхода равно 5 кг. Cчитая расход удобрений нормально распределенной случайной величиной, определить диапазон, в который вносимая доза удобрений попадает с вероятностью 0, 98.

6.5. Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 48 у.е. и стандартным отклонением, равным 6.Определите вероятность того, что в случайно выбранный день обсуждаемого периода цена за акцию была: а) между 40 и 50 у.е. за акцию б) более 60 у.е. за акцию.

6.6. Станок-автомат изготавливает валики, контролируя их диаметр x. Считая, что x распределена нормально, m_x = 10 мм, σ _x = 0, 1 мм, найти интервал, в котором с вероятностью 0, 9973 будут заключены диаметры изготовленных валиков.

6.7. Отклонение стрелки компаса из-за влияния магнитного поля в определенной области Заполярья есть нормальная случайная величина с параметрами (0, 1).Чему равна вероятность того, что абсолютная величина отклонения в определенный момент времени будет больше чем 2, 4?

6.8. Математическое ожидание нормально распределенной случайной величины - количества сыра, используемого для изготовления 100 бутербродов, - равно 1 кг. Известно, что с вероятностью 0, 96 расход сыра на изготовление 100 бутербродов составляет от 900до 1100г. Определить среднее квадратическое отклонение расхода сыра на 100 бутербродов.

6.9. Размер серийно изготавливаемой детали – нормальная случайная величина с параметрами а =40 мм (ГОСТ), σ = 0, 04 мм. Какова вероятность, что размер детали лежит в пределах 39, 94-40, 06?

6.10. Размер серийно изготавливаемой детали – нормальная случайная величина с параметрами а=60 микрон (ГОСТ), σ = 1 микрон. Какова вероятность, что размер детали лежит в пределах 58-62 микрона?

 

Таблица № I

Значения функции Лапласа

x	0, 00	0, 01	0, 02	0, 03	0, 04	0, 05	0, 06	0, 07	0, 08	0, 09
0, 0	0, 000	0, 0040	0, 0080	0, 0120	0, 0160	0, 0199	0, 0239	0, 0279	0, 0319	0, 0359
0, 1	0, 0398	0, 0438	0, 0478	0, 0517	0, 0557	0, 0596	0, 0636	0, 0675	0, 0714	0, 0753
0, 2	0, 0793	0, 0832	0, 0871	0, 0910	0, 0948	0, 0987	0, 1026	0, 1064	0, 1103	0, 1141
0, 3	0, 1179	0, 1217	0, 1255	0, 1293	0, 1331	0, 1368	0, 1406	0, 1443	0, 1480	0, 1517
0, 4	0, 1554	0, 1591	0, 1628	0, 1664	0, 1700	0, 1736	0, 1772	0, 1808	0, 1844	0, 1879
0, 5	0, 1915	0, 1950	0, 1985	0, 2019	0, 2054	0, 2088	0, 2123	0, 2157	0, 2190	0, 2224
0, 6	0, 2257	0, 2291	0, 2324	0, 2357	0, 2389	0, 2422	0, 2454	0, 2486	0, 2517	0, 2549
0, 7	0, 2580	0, 2611	0, 2642	0, 2673	0, 2703	0, 2734	0, 2764	0, 2794	0, 2823	0, 2852
0, 8	0, 2881	0, 2910	0, 2939	0, 2967	0, 2995	0, 3023	0, 3051	0, 3078	0, 3106	0, 3133
0, 9	0, 3159	0, 3186	0, 3212	0, 3238	0, 3264	0, 3289	0, 3315	0, 3340	0, 3365	0, 3389
1, 0	0, 3413	0, 3438	0, 3461	0, 3485	0, 3508	0, 3531	0, 3554	0, 3577	0, 3599	0, 3621
1, 1	0, 3643	0, 3665	0, 3686	0, 3708	0, 3729	0, 3749	0, 3770	0, 3790	0, 3810	0, 3830
1, 2	0, 3849	0, 3869	0, 3888	0, 3907	0, 3925	0, 3944	0, 3962	0, 3980	0, 3997	0, 4015
1, 3	0, 4032	0, 4049	0, 4066	0, 4082	0, 4099	0, 4115	0, 4131	0, 4147	0, 4162	0, 4177
1, 4	0, 4192	0, 4207	0, 4222	0, 4236	0, 4251	0, 4265	0, 4279	0, 4292	0, 4306	0, 4319
1, 5	0, 4332	0, 4345	0, 4357	0, 4370	0, 4382	0, 4394	0, 4406	0, 4418	0, 4429	0, 4441
1, 6	0, 4452	0, 4463	0, 4474	0, 4484	0, 4495	0, 4505	0, 4515	0, 4525	0, 4535	0, 4545
1, 7	0, 4554	0, 4564	0, 4573	0, 4582	0, 4591	0, 4599	0, 4608	0, 4616	0, 4625	0, 4633

Продолжение таблицы № I

x	0, 00	0, 01	0, 02	0, 03	0, 04	0, 05	0, 06	0, 07	0, 08	0, 09
1, 8	0, 4641	0, 4649	0, 4656	0, 4664	0, 4671	0, 4678	0, 4686	0, 4693	0, 4699	0, 4706
1, 9	0, 4713	0, 4719	0, 4726	0, 4732	0, 4738	0, 4744	0, 4750	0, 4756	0, 4761	0, 4767
2, 0	0, 4772	0, 4778	0, 4783	0, 4788	0, 4793	0, 4798	0, 4803	0, 4808	0, 4812	0, 4817
2, 1	0, 4821	0, 4826	0, 4830	0, 4834	0, 4838	0, 4842	0, 4846	0, 4850	0, 4854	0, 4857
2, 2	0, 4861	0, 4864	0, 4868	0, 4871	0, 4875	0, 4878	0, 4881	0, 4884	0, 4887	0, 4890
2, 3	0, 4893	0, 4896	0, 4898	0, 4901	0, 4904	0, 4906	0, 4909	0, 4911	0, 4913	0, 4916
2, 4	0, 4918	0, 4920	0, 4922	0, 4925	0, 4927	0, 4929	0, 4931	0, 4932	0, 4934	0, 4936
2, 5	0, 4938	0, 4940	0, 4941	0, 4943	0, 4945	0, 4946	0, 4948	0, 4949	0, 4951	0, 4952
2, 6	0, 4953	0, 4955	0, 4956	0, 4957	0, 4959	0, 4960	0, 4961	0, 4962	0, 4963	0, 4964
2, 7	0, 4965	0, 4966	0, 4967	0, 4968	0, 4969	0, 4970	0, 4971	0, 4972	0, 4973	0, 4974
2, 8	0, 4974	0, 4975	0, 4976	0, 4977	0, 4977	0, 4978	0, 4979	0, 4979	0, 4980	0, 4981
2, 9	0, 4981	0, 4982	0, 4982	0, 4982	0, 4983	0, 4984	0, 4984	0, 4985	0, 4985	0, 4986
3, 0	0, 4987	0, 4987	0, 4987	0, 4988	0, 4988	0, 4989	0, 4989	0, 4989	0, 4990	0, 4990
3, 1	0, 4990	0, 4991	0, 4991	0, 4991	0, 4992	0, 4992	0, 4992	0, 4992	0, 4993	0, 4993
3, 2	0, 4993	0, 4993	0, 4994	0, 4994	0, 4994	0, 4994	0, 4994	0, 4995	0, 4995	0, 4995
3, 3	0, 4995	0, 4995	0, 4995	0, 4996	0, 4996	0, 4996	0, 4996	0, 4996	0, 4996	0, 4997
3, 4	0, 4997	0, 4997	0, 4997	0, 4997	0, 4997	0, 4997	0, 4997	0, 4997	0, 4997	0, 4998
3, 5	0, 4998	0, 4998	0, 4998	0, 4998	0, 4998	0, 4998	0, 4998	0, 4998	0, 4998	0, 4998
3, 6	0, 4998	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999
3, 7	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999
3, 8	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 4999	0, 5	0, 5	0, 5

 

Таблица № II

Значения нормальной плотности распределения j(x)=

1234567Следующая ⇒

Поделиться: