
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Лекция 3 Динамика системы материальных точек.
Центр масс системы материальных точек.
Из рис.10 и равенства ( 3-1 ) следует, что m2l2 = - m1l1. С учетом этого соотношения из выражения ( 3-3 ) можно определить значение радиуса - вектора R:
Обобщая это выражение для произвольного числа материальных точек, получим:
где Скорость центра масс такой системы определяется дифференцированием ( 3-5 ):
Закон изменения импульса системы материальных точек.
Для простоты рассмотрим движение системы, состоящей из трех точек, на
Складывая эти уравнения, получим:
По третьему закону Ньютона внутренние силы попарно равны по величине и противоположны по направлению ( например, f12 = -f21). Потому сумма всех внутренних сил равна нулю, и
где через Р обозначен суммарный импульс системы. Обобщая ( 3-11 ) для любого числа материальных точек, можно записать следующее выражение:
которое принято называть законом изменения импульса системы материальных точек. Как видно из этого выражения, изменение суммарного импульса определяется равнодействующей всех внешних сил, действующих на систему. Если же эта равнодействующая равна нулю ( или на систему не действуют никакие внешние силы), то суммарный импульс системы остается постоянным. Это следствие уравнения ( 3-12 ) называется законом сохранения импульса. Другим следствием рассмотренного закона изменения импульса служит теорема о движении центра масс, которая утверждает, что центр масс системы материальных точек под действием внешних сил движется как материальная точка суммарной массы, к которой приложены все внешние силы, и записывается в таком виде: МА = Доказательство этого утверждения следует из сравнения определения ускорения центра масс( 3-8 ) и выражения ( 3-13 ). Примерами закона сохранения импульса могут служить отдача при стрельбе из огнестрельного оружия, реактивное движение, перемещение осьминогов и т.п. Лекция 4. Динамика твердого тела. Кинематические соотношения. Твердое тело можно рассматривать как систему материальных точек, жестко скрепленных друг с другом. Отсутствие такого закрепления существенно затруднило бы описание движения всего конгломерата точек. Для полного описания движения одной точки необходимо знать ее три координаты, поэтому для N точек число необходимых координат, а следовательно, и число уравнений для их определения составило бы 3N. Так как число N может быть как угодно большим, то возможности строгого решения системы из 3N уравненийвесьма ограничены.
§ 4-2. Определение момента силы.
Для описания динамики вращательного движения твердого тела необходимо ввести понятие момента силы.При этом надо различать понятия момента силы
Рис.11. Момент силы от- Носительно точки. | относительно точки и относительно оси. Если сила f приложена к материальной точке А(см. рис.11), то моментом силы М относительно произвольной точки О называется векторное произведение радиуса-вектора r, проведенного из точки О к точке А, и вектора силы:
М = [ r f ]. ( 4-2 )
Модуль векторного произведения 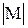 = r f sin a, а на-
правление вектора М определяется правилом правого буравчика: направление первого вектора r по кратчай- = r f sin a, а на-
правление вектора М определяется правилом правого буравчика: направление первого вектора r по кратчай-
|
шему пути вращается к направлению второго вектора f, а движение оси буравчика
                           zMz
f
f
O f
r a
А
Рис.12. Момент силы от- носительно оси. zMz
f
f
O f
r a
А
Рис.12. Момент силы от- носительно оси.
| при этом вращении показывает направление вектора М. Моментом силы относительно произвольной оси z называется векторное произведение радиуса-вектора r и составляющей f силы f, приложенной в точке А: М = [ r f ], ( 4-3 ) где составляющая f представляет собой проекцию си- лы f на плоскость, перпендикулярную оси z и проходящую через точку А, а r - радиус- вектор точки А, ле- жащий в этой плоскости. |
Последнее изменение этой страницы: 2017-03-16; Просмотров: 375; Нарушение авторского права страницы