
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Отражение частиц от потенциальной ступеньки. Туннельный эффект.
Так говорит классическая механика Рассмотрим случай Решение ур. Шрёдингера покажет, что происходит с реальными частицами. С учетом того, что в первой области
Первая область: Решения этих уравнений имеет вид Первое слагаемое в В точке
Окончательно волновые функции для первой и второй областей имеют вид:
Перейдем к рассмотрению случая, когда энергия частицы больше высоты ступеньки ( Ур. Шрёдингера для первой и второй областей выглядит также. С учетом того, что
Оба решения представляют собой суммы падающей и отраженной волн. Так как во второй области нет отраженной волны, то
Мы получили, что коэффициент Определим для потенциальной ступеньки коэффициенты отражения R и прохождения Т. Пусть на ступеньку из первой области падает пучок частиц. Скорость частиц в первой области Коэффициент отражения определим как отношение интенсивностей отраженного и падающего потоков: Туннельный эффект.
 Проанализируем теперь движение квантовой частицы. Пусть Проанализируем теперь движение квантовой частицы. Пусть  , тогда 1 – область слева от барьера, 2 - область барьера, 3 - область справа от барьера. Волновые функции частицы в этих областях обозначим соответственно , тогда 1 – область слева от барьера, 2 - область барьера, 3 - область справа от барьера. Волновые функции частицы в этих областях обозначим соответственно  . Запишем уравнение Шрёдингера для каждой области: Первая область . Запишем уравнение Шрёдингера для каждой области: Первая область 
 Вторая область: Вторая область:  . Третья область: . Третья область:  . Решения этих уравнений имеют вид (очевидно . Решения этих уравнений имеют вид (очевидно 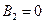 и и  ): ):  , ,  , , 
Так как в первой области решение содержит отраженную волну, то это означает, что частица имеет конечную вероятность отражения от барьера (у классической частицы вероятность равна 1). Так как в третьей области есть прошедшая волна, то у частицы есть вероятность прохождения за барьер (с классической точки зрения в принципе не может быть). Такая способность квантовых частиц проникать сквозь потенциальный барьер при
|
Последнее изменение этой страницы: 2017-03-17; Просмотров: 877; Нарушение авторского права страницы