Определение «лишних» неизвестных

Способом сравнения перемещений

При выборе основной системы за «лишние» неизвестные при расчете статически неопределимых балок способом сравнения перемещений принимаются опорные реакции и моменты в результате отбрасывания соответствующих «лишних» опорных связей.

Недостающие уравнения, так называемые уравнения совместности перемещений, число которых соответствует числу «лишних» неизвестных, составляются по условиям деформации.

Основным приемом раскрытия статической неопределимости балок является составление дополнительных уравнений совместности перемещений (прогибов и углов поворота) опорных сечений и приравниванием их к нулю, так как в заданной системе по направлению неизвестных опорных реакций и моментов наложены «лишние» связи. Решение этих дополнительных уравнений перемещений может быть выполнено различными способами: интегрирования дифференциального уравнения изогнутой оси методом начальных параметров, применением теоремы Кастильяно, интеграла Мора и способа Верещагина. Определив «лишние» неизвестные, из уравнений статики найти остальные реакции опор. Затем построить эпюры поперечной силы и изгибающего момента.

Пример расчета статически неопределимой балки

Для заданной статически неопределимой балки требуется:

Выяснить степень статической неопределимости балки (рис. 13а)

Определить «лишние» неизвестные двумя способами:

а) уравнением трех моментов;

б) способом сравнения перемещений.

Построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать по сортаменту двутавровое сечение, если [s]=160МПа.

Определить эффективность (по расходу металла) статически неопределимой балки по сравнению со статически определимой, полученной определенным способом из заданной.

По эпюре изгибающих моментов изобразить форму изогнутой оси.

Применение теоремы о трех моментах.

Решение.

1. Основную систему для расчета неразрезной балки получим, если над всеми промежуточными опорами врежем шарниры, а в качестве «лишних» неизвестных примем изгибающие моменты в надопорных сечениях М_n. В данном примере балка дважды статически неопределима. Неизвестными являются опорные моменты М₁ и М₂ .

Опорный момент М₃ = -40 кНм, М₀ = 0 (рис. 13б). Расчетная схема балки с нумерацией опор и пролетов показана на рис. 13а.

2.. Эпюра изгибающих моментов в каждом пролете от внешней нагрузки представлена на рис. 13в. Момент на опоре 3 от силы Р₁ на конце консоли не считается нагрузкой, действующей в третьем пролете.

3. Составим уравнения трех моментов попарно для двух смежных пролетов слева направо:

 

Рис. 13

 

(6.3.1)

(6.3.2)

После сокращения уравнений (6.3.1) и (6.3.2) и, учитывая, что М₀ = 0 и М₃= –40 кНм, получаем:

20М₁+4М₂= -330

4М₁+18М₂= -665

Решив эти уравнения, найдем:

М₁= -9, 535 кНм; М₂= -34, 825 кНм

После определения моментов М₁ и М₂ задача стала статически определимой.

4. Найдем опорные реакции. Для этого составим уравнения моментов и моментов всех сил поочередно слева или справа относительно опор неразрезной балки:

 

Проверка правильности вычисления реакций:

R₀ + R₁ + R₂ + R₃ -P-P₁-q = 0;

-11, 6 + 25, 4 + 75, 2 +71 - 40 - 20 - 20 × 5 = 0

0º 0

Реакции определены правильно.

5. Построение эпюры поперечных сил Q (рис. 14)

Пролет 0–1:

Q = -R₀ = -11, 6 кН;

Пролет 1–2: Q = -R₀ + R₁ = -11, 6 + 25, 4 = 13, 8 кН

Q = -R₀ + R₁- P = -11, 6 + 25, 4 – 40 = 26, 2 кН;

Консоль: Q = +Р₁ = 20 кН

Пролет 2-3: Q = +P₁- R₃ + qz

При Z = 0 Q = +P₁ - R₃ = 20 - 71 = -51 кН;

При Z = 5 Q = +P₁ - R₃ + qz = 20 - 71 + 20× 5 = 49 кН.

Определим координату Z, при которой изгибающий момент в пролете 3-2 будет экстремальным

Q = P₁ - R₃ + qz = 0;

 

Рис. 14

 

6. Построение эпюры изгибающих моментов М (рис. 14б)

Пролет 0-1 0 £ z £ M = -R₀× z;

 

Z
M		-34, 8

M=-Rz+M;

Z
M	25, 2	-9, 535

Пролет 1-2:

Z
M		-35, 0

Консоль: М=-P₁ z

Z
M		-40

Пролет 3-2:

Z			2, 55
M	-40	-35

7. Определение «лишних» неизвестных способом сравнения перемещений

Основная система показана на рис. 15а.

В качестве «лишних» неизвестных при решении примера способом сравнения перемещений примем реакции на опорах 0 и 3, т.е. R₀ и R₃. Составим уравнения перемещений (прогибов) опорных сечений 1 и 3 и приравняем их к нулю. Используем интеграл Мора, вычисленный по способу Верещагина. Для этого в основной системе в сечениях 1 и 3 прикладываем единичные силы Р₁=1. Строим эпюры изгибающих моментов в основной системе от действия внешних сил и моментов и от единичных сил Р₁ = 1 (рис. 15б).

8. Для определения реакций R₀ и R₃ составим выражения прогибов на опорах 0 и 3 и приравняем их к нулю

 

Рис. 15

 

Здесь w - площадь эпюры изгибающих моментов от заданных сил.

М⁰_с – ординаты эпюры изгибающих моментов от единичной Р_i нагрузки в сечениях 0 и 3 под центром тяжести площади w_i и тогда 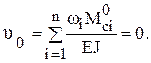Подставляя значения ω _i и , получим

 

 

 

 

 

 

 

 

 

 

После сокращений уравнений получим

120R₀ + 20R₃ - 30 = 0

60R₀+ 225R₃ - 15287, 5 = 0

Решив уравнение, найдем

R₀ = -11, 6 кН; R₃ = 71, 0 кН

9. Для определения реакций R₁ и R₃ определяем изгибающий момент на опоре 2.

Составим уравнения моментов относительно опорных сечений

или

 

R₁ = 25, 4 кН.

или

Таким образом, величины реакций при решении задачи обоими способами соответственно равны

10. Подбор сечения двутавровой неразрезной балки из условия прочности при изгибе

Тогда требуемый момент сопротивления

Принимаем двутавр № 22а, у которого W_х = 254 см³; площадь поперечного сечения F = 32, 8 см².

Действительное нормальное напряжение

Расхождение в процентах

(недогрузка)

11. Исследование влияния лишних опор на прочность балки.

Образуем статически определимую балку из заданной статически неопределимой (рис. 16).

Определим реакции опор

0

или

кН;

или

кН

86 + 74 – 40 – 20 – 20 · 5 = 0 0 ≡ 0. Реакция определена правильно.

Рис. 16

Рис. 17

 

Построим эпюры Q и М.

Пролет 1–2:

Q = -Р = -40 кН;

Пролет 2-3: Q = -P +R2 -qz;	Z
M		-54

Определим координату Z, при которой изгибающий момент в пролете 3–2 будет экстремальным

Q = -P + R₂ - qz = 0

Консоль: Q = P₁ = 20 кН;

Пролет 0–1 и 1–2:

М = М= 60 кНм;

М = М - Pz;	z
M		-20

Пролет 2–3:

М = М

Z			2, 3
M	-20	-40

Консоль М = -Р× z

z
M		-40

Эпюры Q и М показаны на рисунке 17.

Подбор сечения двутавровой статически определимой балки.

Требуемый момент сопротивления

Принимаем двутавр № 27, у которого W_x =3 71 см³; площадь поперечного сечения F = 40, 2 см².

Перерасход материала составит

 

· 100 = · 100 = 22, 5%

12. По эпюре изгибающих моментов на рис. 14в представлена форма изогнутой оси балки.

Сложное сопротивление

Общие замечания

Сопротивление называется сложным, когда стержень одновременно испытывает несколько простых напряженно–деформированных состояний. К простым относятся: осевое растяжение и сжатие, кручение, плоский изгиб.

При расчетах на сложное сопротивление обычно исходят из принципа независимости действия сил, т.е. считают, что напряжение и деформация есть алгебраическая и геометрическая сумма результатов простых напря­женно-деформированных состояний, и они не зависят от последователь­ности приложения сил.

При расчете сложного сопротивления стержня важно найти сечения и точки в них, где результаты действия простых напряженно-дефор­ми­ро­ван­ных состояний велики и имеют один знак. Это будут опасные точки, по состоянию в них проверяют прочность стержня.

В этом разделе рассматриваются два вида сложного сопротив­ления: внецентренное сжатие или растяжение и изгиб с кручением.

Внецентренное растяжение или сжатие – это изгиб в двух плоскостях относительно главных центральных осей инерции (косой изгиб) и центральное растяжение - сжатие. Нормальные напряжения в любой точке сечения стержня в данном случае определяются по формуле

(7.1.1)

где Р – сила, действующая по нормали к поперечному сечению, вызы­вающая осевое сжатие и изгиб моментами Р·у_р и Р·х_р

х_р и у_р – координаты точки приложения силы;

х и у– координаты точки, в которой определяются нормальные напряжения;

i_x и i_y – радиусы инерции поперечного сечения относительно главных центральных осей инерции поперечного сечения X и Y со­ответственно.

F – площадь поперечного сечения.

В формуле (7.1.1) первое слагаемое с учетом множителя перед скобкой – это нормальные напряжения осевого сжатия; второе это нормальные напряжения от изгиба в плоскости yоz; третье - напряжение от изгиба в плоскости XOZ.

Формула (7.1.1) написана для сжимающей силы Р, если сила Р –растягивающая, то знак (–) заменяется на (+).

Изгиб с кручением – это напряженно-деформированное состояние, когда в поперечном сечении стержня могут действовать все шесть внутрен­них силовых факторов. Однако влияние поперечных сил в направлении двух главных осей поперечного сечения мало скажется на суммарных нап­ряжениях в опасных точках, а влияние нормальной силы учитывается только при стесненном кручении. С задачами на изгиб с кручением мы сталкиваемся при расчете круглых валов. В этом случае все центральные оси главные, и по­этому из­гиб под действием внешних сил в разных плоскостях можно свести к изгибу в одной плоскости.

Опасными точками в сечении, где действует максимальный изги­бающий момент и крутящий момент, будут точки на поверхности и вала на максимальном расстоянии от оси вала в плоскости изгиба. В этих точках будут одновременно действовать нормальные и касательные напряжения. Используя условия прочности по третьей нории (теории наибольших каса­тельных напряжений), расчетная формула для эквивалентных напряжений имеет такой же вид как и при плоском поперечном изгибе (частный случай плоского напряженного состояния). При этом расчетный момент определяется по формуле М_р = .

Для нахождения требуемого диаметра вала достаточно в условие проч­ности, записанное в такой форме: σ _экв = подставить значения рас­четного момента, допускаемых нормальных на­пряжений и осевого момента сопротивления для круглого сечения и решить его относительно диаметра.

В последующих подразделах 7.2 и 7.4 даны методические указания к решению задач на внецентренное сжатие и на изгиб с круче­ни­ем соответственно, а в подразделах 7.3 и 7.5 -примеры расчета.

⇐ Предыдущая12345678Следующая ⇒

Поделиться: