Каноническая форма задачи линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В том случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Она может быть представлена в координатной, векторной или матричной записи.

1. Каноническая задача линейного программирования в координатной записи имеет вид

(1.6)

.

В более компактной форме данную задачу можно записать, используя знак суммирования,

(1.7)

2. Каноническая задача линейного программирования в векторной записи имеет вид

(1.8)

где ,

.

3. Каноническая задача линейного программирования в матричной записи имеет вид

(1.9)

где

, .

Здесь А – матрица коэффициентов системы уравнений, Х – матрица-столбец переменных задачи, – матрица-столбец правых частей системы ограничений.

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной записи имеют вид

(1.10)

или

(1.11)

1.4. Приведение общей задачи линейного программирования
к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако при составлении математических моделей экономических задач ограничения в основном формируются в системы неравенств, поэтому необходимо уметь переходить от системы неравенств к системе уравнений. С этой целью докажем следующую теорему.

Теорема 1.1. О замене неравенства уравнением. Каждому решению неравенства

(1.12)

соответствует единственное решение уравнения

(1.13)

и неравенства

, (1.14)

и, наоборот, каждому решению уравнения (1.13) и неравенства (1.14) соответствует единственное решение неравенства (1.12).

Доказательство. Пусть – решение неравенства (1.12), тогда . Обозначим разность правой и левой частей этого неравенства через , т. е.

.

Очевидно . Подставим в уравнение (1.13) вместо переменных значения , получим

.

Таким образом, удовлетворяет уравнению (1.13) и неравенству (1.14). Значит доказана первая часть теоремы.

Пусть теперь удовлетворяет уравнению (1.13) и неравенству (1.14), т. е. имеем

и

Отбрасывая в левой части последнего равенства неотрицательную величину , получаем

,

т. е. удовлетворяет неравенству (1.12). Теорема доказана.

Если неравенство , то дополнительную неотрицательную переменную необходимо ввести в его левую часть со знаком минус, т. е. .

Неотрицательные переменные, вводимая в ограничения неравенства для превращения их в уравнения, называются дополнительными переменными. Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значение.

В том случае, когда задача имеет произвольно изменяющиеся переменные, то любую такую переменную заменяют разностью двух неотрицательных переменных, т. е. , где и .

Иногда возникает необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций на оптимальных решениях отличаются только знаком.

Пример 1.1. Привести к каноническому виду задачу линейного программирования.

Д

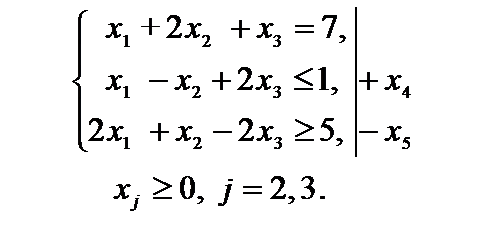
Решение. Перейдем к задаче на отыскание максимума целевой функции. Для этого изменим знаки коэффициентов целевой функции. Для превращения в уравнения второго и третьего неравенств системы ограничений введем неотрицательные дополнительные переменные (на математической модели эта операция отмечена буквой Д). Переменная вводится в левую часть второго неравенства со знаком " +", так как неравенство имеет вид . Переменная вводится в левую часть третьего неравенства со знаком " -", так как неравенство имеет вид . В целевую функцию переменные вводятся с коэффициентом, равным нулю. Переменную , на которую не наложено условие неотрицательности заменяем разностью , . Записываем задачу в каноническом виде

.

В некоторых случаях возникает необходимость приведения канонической задачи к симметричной задаче. Рассмотрим пример.

Пример 1.2. Привести к симметричному виду задачу линейного программирования

.

Решение. Методом Жордана-Гаусса приведем систему уравнений-ограничений задачи к равносильной разрешенной. Одновременно разрешенные неизвестные исключим из целевой функции. Для этого в таблице решения задачи (табл. 1.1) наряду с коэффициентами уравнений системы ограничений в дополнительной строке запишем коэффициенты целевой функции. В последнем столбце дополнительной строки (на месте правой части уравнений) запишем свободный член целевой функции, равный нулю. При вычислениях учитываем, что разрешающий элемент в последней строке (в целевой функции) выбирать нельзя.

Т а б л и ц а 1.1

x1	x2	x3	x4	b
	–2				x(–3)	x(–1)
–7			–4		+
	–5				Целевая функция
	–2
–16			–16	–16
	–3		–2	–6
	–2				+
–1			–1	–1	´ 2 ´ 3
	–3		–2	–6	+
–1			–1	–1
–2			–5	–9

 

Число -9, полученное в последнем столбце последней строки таблицы необходимо записать в целевую функцию с противоположным знаком. В результате данных преобразований задача принимает следующий вид:

.

Так как переменные неотрицательные, отбросив их, можно записать задачу в симметричном виде

.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: